具体数学-学习笔记第一章递归问题

1.1 河内塔

思想:简化问题，先研究小的情形

方法:命名并求解-引入记号T_n 称T_n为根据卢卡斯规则将n个圆盘从一根桩柱移动到另一个所需要的最少移动次数。

过程:设有n个圆盘由A—>B 需要 I.先移动圆盘（1∼n-1）—>C II.移动圆盘 n —>B III.移动圆盘（1∼n-1）—>B 得T_n≤2T_n-1 + 1,n>0

书中也给出了第二个情况即圆盘n移动多与一次，此时可得T_n≥2T_n-1 + 1, n>0

两不等式与T₀ = 0联合得——T₀=0 T_n=2T_n-1+1,n>0（<——这样的一组式子称为递归式）

过程:a.研究小的情形

b.对有意义的量求出数学表达式并给出证明

c.对数学表达式求出封闭形式并给出证明

递归式求解: 方法:数学归纳法累加法累乘法构造法代定系数法特征根法

要注意最少这个限定词，这是式子的基础

书中给出的第二种情况难以理解和说明，可以直接认为T_n=2T_n-1+1

1.2 平面上的直线

思路:平面上的任意两条直线不平行即相交，保证任意一条直线与其他直线都相交即可得到所界定区域的最大个数，而且第n条新直线都会与n-1条旧直线形成n-1个交点，这n-1个交点可以形成（n-3）条线段和2条射线，每一条线段可以将有界区域一分为2，每一条射线可以将无界区域一分为2

由此可以得出界定区域L L_n = L_n-1 + n ,n>0 带入展开（如下图）后可得L_n = n(n+1)/2,n>0

同理，可以求出有界区域得数量I 因为第n条新直线都会与n-1条旧直线形成n-1个交点，这n-1个交点可以形成（n-2）条线段，这n-2个线段可以新形成n-2个有界区域，可以得出I_n = I_n-1 + (n-2) ,n>0

另外，收回直线多余部分可以得到有界区域，移动直线到一点可以得到无界区域(设无界区域数量为E)，由界定区域数量=有界数量+无界数量也可以得到有界区域数量

下面开始推广，首先是一维中的情况。

在一维直线上时每次划线切割都只是增加一个区域，最后可以得到区域数量X的递推公式与封闭形式

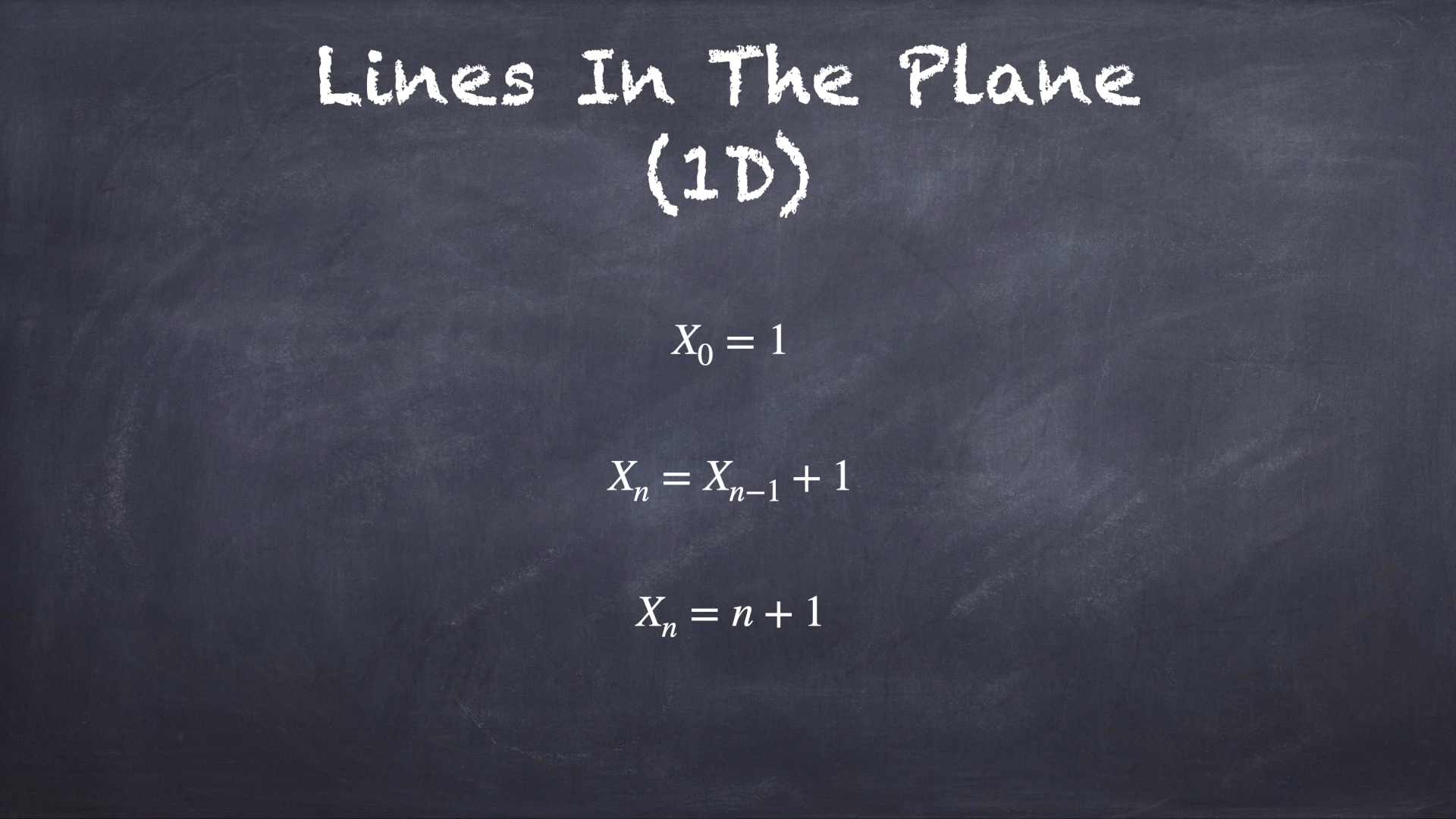
其次是二维中的情况。

二维中的情况和上文相同，都是在平面上划线，而且由上文可知，第n条新直线可以与前n-1条旧直线相交，从而得到n-1个交点，n-1个点把这条直线分为n个部分，每一个部分都将它所经过的区域一分为二，同时得到n个新的区域，并且二维中的每一条直线都可以看作一维中的情况。因为L_n = L_n-1 + n ,n>0 n可以由X_n-1代替所以可以得出L_n = L_n-1 + X_n-1,n>0

由下图可以直观感受到，当无直线时无交点 L₀=X₀ 当一条直线时候直线L₁有0个交点，无直线无交点L₁=X₀+X₀，当二条直线时候直线L₂有1个交点，直线L₁有0个交点，无直线无交点 L₂=X₀+X₀+X₁，当三条直线时候直线L₃有两个交点，直线L₂有1个交点，直线L₁有0个交点，无直线无交点 L3 = X₀+X₀+X₁+X₂