【11.19 NOIP模拟赛】总结

【11.19 NOIP模拟赛】总结

T1 集合

给定 \(n\)，求 \(\{1...n\}\) 所有非空子集的和的积。

\(n\le200\)

DP 求和为 \(i\) 的方案数 \(f_i\)，答案为 \(\prod\limits_{i=1}^{n(n+1)/2}i^{f_i}\)

注意 \(f_i\) 为指数，应对 \(P-1\) 取模（费马小定理）

T2 出租

有 \(n\) 栋楼，每栋楼有 \(k\) 个房间，有 \(m\) 次操作，每次操作加入或移除 \(y_i\) 个理想位置为 \(x_i\) 的人，这 \(y_i\) 个人必须安排在 \([x_i,x_i+d]\) 的楼中，问每次操作后存不存在合法方案。

\(1\le n,m,d\le 5\times 10^5,0\le k,y\le 10^9,1\le x \le n-d\)

一道很厉害的猜结论题（那么是谁场上想了将近两个小时呢）

不难发现无解的一个充分条件：\(\sum{v_i}>n\times k\)

这样约束性显然太弱了，那么先区间缩小看看？

一个区间 \([l,r]\) 无解的充分条件：\(\sum\limits_{i=l}^r{v_i}>(r-l+1+d)\times k\)

注意： 区间内靠右的人可以放在区间外面的 \(d\) 个位置，所以要 \(+d\)

然而这样的约束还是太弱了，不妨猜测：

当前局面无解，当且仅当 存在子区间 \([l,r]\)，满足：\(\sum\limits_{i=l}^r{v_i}>(r-l+1+d)\times k\)

看起来又对又不对的，然而自己手搓几个样例，会发现举不出反例（）

于是就好做了，移项得：\(\sum\limits_{i=l}^{r}{(v_i-k)}>k\times d\)

那么线段树维护一下最大子段和就做完了 qwq

T3 连通块

求一颗树的最大权连通块，但必须满足 \(m\) 条形如 ” \(u,v\) 的 \(dfs\) 序在连通块内不能连续 “ 的限制条件。

每个点的儿子遍历顺序给定，\(n\le 10^5,m\le 21,|v_i|\le10^9\)

首先讲下 80pts（保证树随机生成）的神仙做法：（后面有图）

什么意思呢？就是拆点后把连通块的 dfs 序转化成一个 DAG

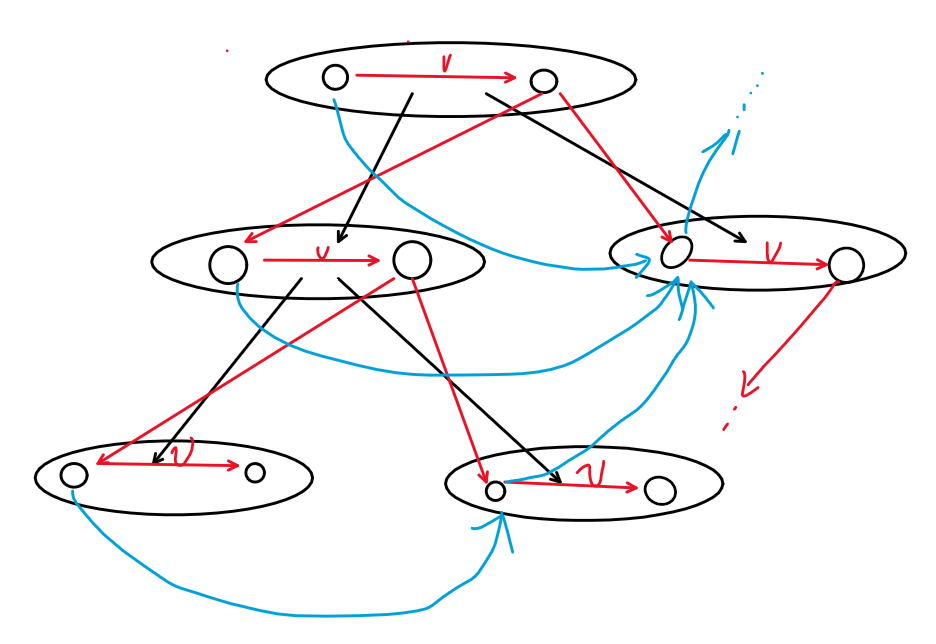
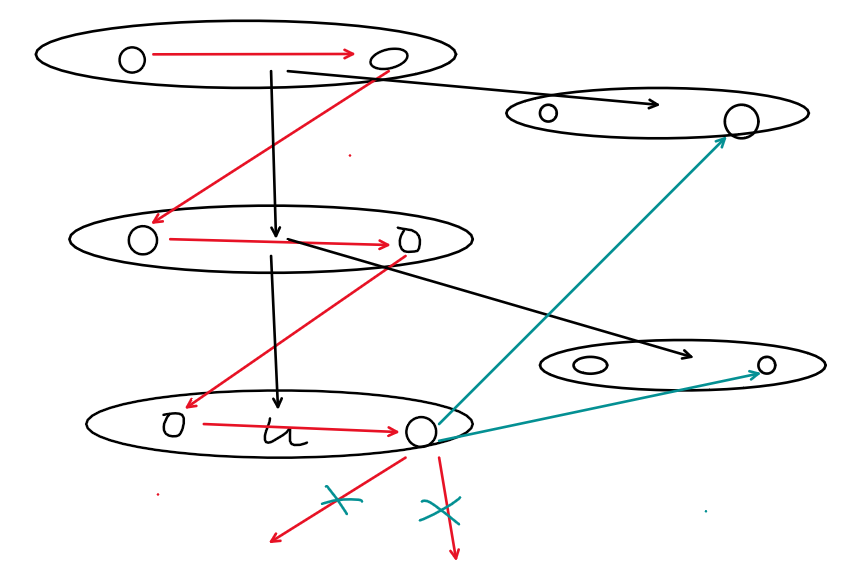
对着图自行理解一下，总复杂度 \(O(nm\log n)\) 级别

接下来是正解：

设 \(f_{i,j}\) 表示 \(i\) 子树内，最后一个 \(dfs\) 序为 \(j\) 的答案。

直接上图吧

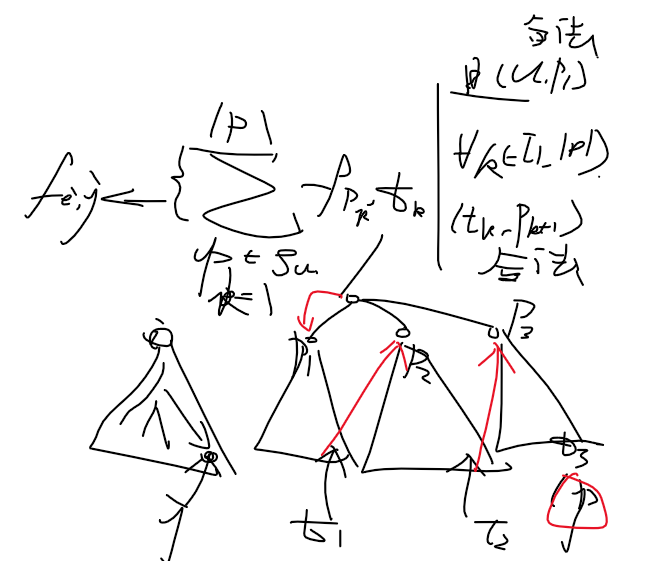
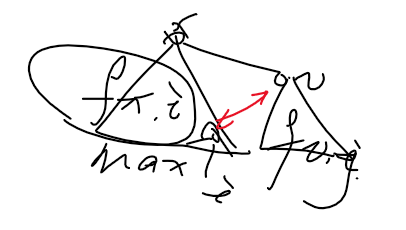
所以我们可以直接这么转，类似于树形背包，对于每个顺序遍历的儿子 \(v\)：

\[f_{u,i}=\max(f_{u,i},\max\{f_{u,j}+f_{v,i}|\text{the (i, j) is legal}\}) \]

dp 中直接记录 \(n\) 个点的 \(dfn\) 肯定是不行的，于是我们发现与约束条件无关的点我们并不关心，再注意到 \(m\) 很小，于是可以 只给有约束点编号 （类似虚树），无关点编号 \(0\)。

时空复杂度 \(O(nm)\)，可以通过此题