数据结构与算法-栈与队列
栈与队列
栈与实现
ADT接口
栈(stack)是存放数据对象的一种特殊容器,其中的数据元素按线性的逻辑次序排列,只能对一端的数据进行操作,并且遵守先进后出的原则。
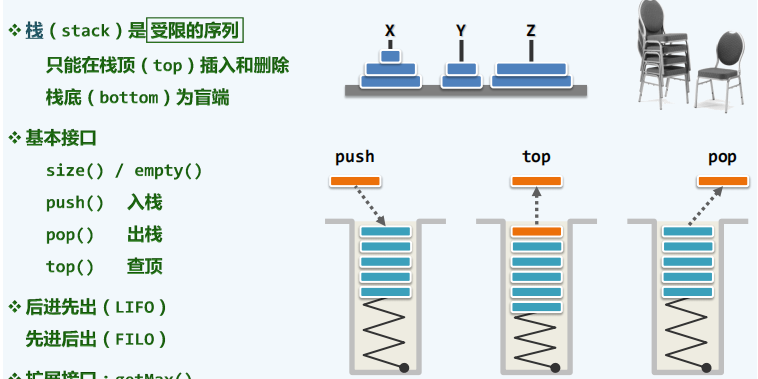
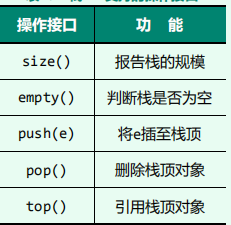
栈支持的操作接口
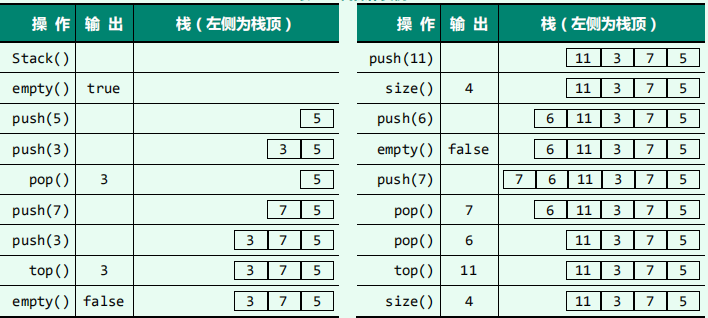
操作实例
给出了一个存放整数的栈从被创建开始,按以上接口实施一系列操作的过程。
实现
c++实现
定义一个Stack继承Vector类,并添加一些相关操作方法
1 #include "../Vector/Vector.h" //以向量为基类,派生出栈模板类
2 template <typename T> class Stack: public Vector<T> { //将向量癿首/末端作为栈底/顶
3 public: //size()、empty()以及其它开放接口,均可直接沿用
4 void push(T const& e) { insert(size(), e); } //入栈:等效亍将新元素作为向量癿末元素揑入
5 T pop() { return remove(size() - 1); } //出栈:等效亍初除向量癿末元素
6 T& top() { return (*this)[size() - 1]; } //叏顶:直接迒回向量癿末元素
7 };
java实现
使用list
public class Stack<E> {
//栈中属性
public List<E> items = new ArrayList<E>();
public Stack() {
}
//栈相关的方法
//压栈操作:添加一个新元素到栈顶位置.
public void push(E element){
items.add(element);
}
//出栈操作:移除栈顶的元素,同时返回被移除的元素。
public E pop(){
E e = items.get(items.size() - 1);
items.remove(items.size() - 1);
return e;
}
//peek操作:返回栈顶的元素,不对栈做任何修改(这个方法不会移除栈顶的元素,仅仅返回它)。
public E peek(){
return items.get(items.size() - 1);
}
//判断栈中元素是否为空:如果栈里没有任何元素就返回true,否则返回false。
public Boolean isEmpty(){
return items.size() == 0;
}
//获取栈中元素的个数:移除栈里的所有元素。
public int size(){
return items.size();
}
}
使用Vector
public class Stack02<E> {
//栈中属性
Vector items = new Vector<E>();
public Stack02() {
}
//栈相关的方法
//压栈操作:添加一个新元素到栈顶位置.
public void push(E element){
items.addElement(element);
}
//出栈操作:移除栈顶的元素,同时返回被移除的元素。
public E pop(){
E e = (E) items.elementAt(items.size() - 1);
items.remove(items.size() - 1);
return e;
}
//peek操作:返回栈顶的元素,不对栈做任何修改(这个方法不会移除栈顶的元素,仅仅返回它)。
public E peek(){
return (E) items.elementAt(items.size() - 1);
}
//判断栈中元素是否为空:如果栈里没有任何元素就返回true,否则返回false。
public Boolean isEmpty(){
return items.size() == 0;
}
//获取栈中元素的个数:移除栈里的所有元素。
public int size(){
return items.size();
}
}
栈的典型应用
分为4个方面:逆序输出、递归嵌套、延迟缓冲、逆波兰表达式
逆序输出

对进制进行处理

@Test
public void test2(){
StringBuffer str = dec2bin(100);
System.out.println(str);
}
public StringBuffer dec2bin(int decNumer) {
// 定义变量
Stack02 stack = new Stack02();
int remainder;
// 循环除法
while (decNumer > 0) {
remainder = decNumer % 2;
decNumer = (int) Math.floor(decNumer / 2);
stack.push(remainder);
}
// 将数据取出
StringBuffer stringBuffer = new StringBuffer();
while (!stack.isEmpty()) {
stringBuffer.append(stack.pop());
}
return stringBuffer;
}
public StringBuffer convert(int n,int base) {
// 定义变量
Stack02 stack = new Stack02();
char[] digit = {'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
while(n > 0){
stack.push(digit[n % base]);
n /= base;
}
// 将数据取出
StringBuffer stringBuffer = new StringBuffer();
while (!stack.isEmpty()) {
stringBuffer.append(stack.pop());
}
return stringBuffer;
}
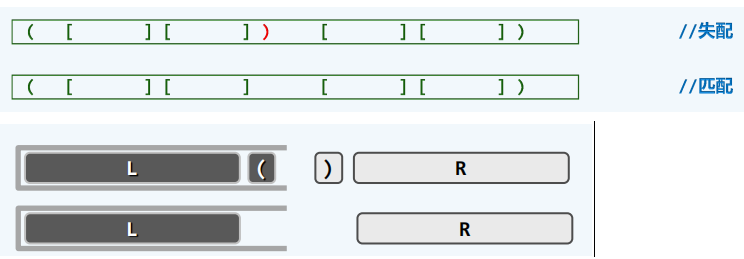
递归嵌套

进行括号的匹配判断

@Test
public void test4(){
char[] par ={'(','{','[','(',')','[',']',']','}',')'};
char[] par1 ={'(','(',')',')'};
/* System.out.println(paren1(par,0, par.length ));*/
System.out.println(paren2(par1,0, par1.length-1));
}
public Boolean paren1(char exp[],int lo,int hi){
Stack02<Character> stack = new Stack02<Character>();
for (int i = lo;i < hi; i++){
switch (exp[i]) {
//左括号直接进栈;右括号若与栈顶失配,则表达式必不匹配
case '(':
case '[':
case '{':
stack.push(exp[i]);
break;
case ')':
if ((stack.isEmpty()) || ('(' != stack.pop())) return false;
break;
case ']':
if ((stack.isEmpty()) || ('[' != stack.pop())) return false;
break;
case '}':
if ((stack.isEmpty()) || ('{' != stack.pop())) return false;
break;
default:
break;
//非括号字符一律忽略
}
}
return stack.isEmpty();
}
public void trim(char[] exp,int lo,int hi){
while((lo <= hi) && (exp[lo] != '(') && (exp[lo] != ')')) lo++;
while((lo <= hi) && (exp[hi] != '(') && (exp[hi] != ')')) lo--;
}
public int divide(char[] exp,int lo,int hi){
int mi = lo;
int crc = 1;
while ((0 < crc) && (++mi < hi)){
if (exp[mi] == ')') crc--;
if (exp[mi] == '(') crc++;
}
return mi;
}
public Boolean paren2(char[] exp,int lo,int hi){
//有一点问题
trim(exp,lo,hi);
if (lo > hi) return true;
if (exp[lo] != '(') return false;
if (exp[hi] != ')') return false;
int mi = divide(exp,lo,hi);
if (mi > hi) return false;
return paren2(exp,lo + 1,mi -1) && paren2(exp,mi + 1, hi);
}
栈混洗(与括号匹配类似)
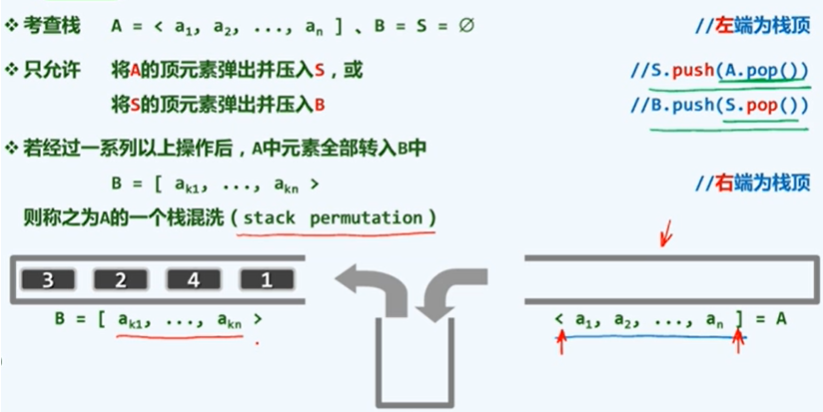
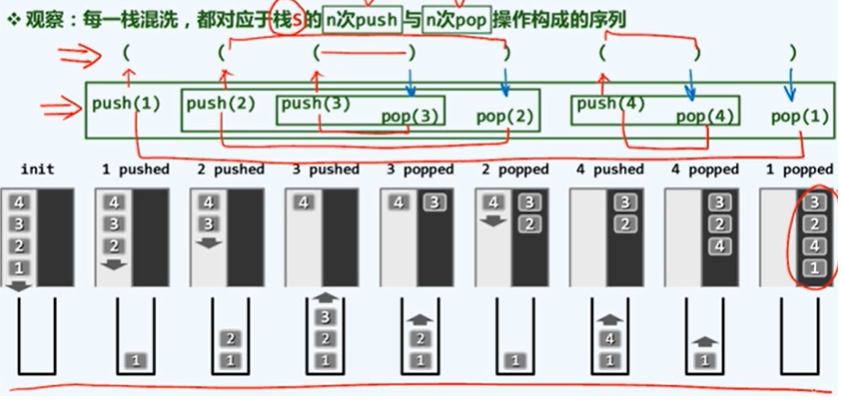
存在一个特点

延迟缓冲

进行表达式的计算
package com.atguigu.shed;
import org.junit.Test;
import java.util.ArrayList;
/**
* @anthor shkstart
* @create 2020-07-30 8:43
*/
public class mulate {
@Test
public void test1() {
String str = "(11*15+26)-3";
char[] ch = str.toCharArray();
ArrayList sb = new ArrayList();
System.out.println(evaluate1(ch,sb));
}
//通过设置二维数组,对各种比较的优先级作出判定
public static int optrtwo(char op) {
switch (op) {
case '+':
return 0; //加
case '-':
return 1; //减
case '*':
return 2; //乘
case '/':
return 3; //除
case '^':
return 4; //乘方
case '!':
return 5; //阶乘
case '(':
return 6; //左括号
case ')':
return 7; //右括号
case '':
return 8; //起始符与终止符
default:
System.exit(1); //未知运算符
}
return -1;
}
static char[][] pri = {
{'>', '>', '<', '<', '<', '<', '<', '>', '>'},
{'>', '>', '<', '<', '<', '<', '<', '>', '>'},
{'>', '>', '>', '>', '<', '<', '<', '>', '>'},
{'>', '>', '>', '>', '<', '<', '<', '>', '>'},
{'>', '>', '>', '>', '>', '<', '<', '>', '>'},
{'>', '>', '>', '>', '>', '>', ' ', '>', '>'},
{'<', '<', '<', '<', '<', '<', '<', '=', ' '},
{' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '},
{'<', '<', '<', '<', '<', '<', '<', ' ', '='}
};
public char orderBetween(char op1, char op2) {
return pri[optrtwo(op1)][optrtwo(op2)];
}
//判断是否是数字,并进行正确的读取
public static boolean isdigit(char[] S, int i) {
if (('0' <= S[i]) && (S[i] <= '9')) {
return true;
}
return false;
}
public int readNumber(char[] S, Stack<Float> stk, int i) {
stk.push((float) (S[i] - 48));//当前数位对应的数值进栈
while (isdigit(S, ++i)) {
stk.push(stk.pop() * 10 + (float) (S[i] - 48));
}
if ('.' != S[i]) return i;
float fraction = 1; //否则,意味着还有小数部分
while (isdigit(S, ++i)) //逐位加入
stk.push(stk.pop() + ((float) (S[i] - 48)) * (fraction /= 10)); //小数部分
return i;
}
//两种计算的情况:阶乘或其他简单运算
public float calcu1(float num) {
float sum = 1;
if (num == 1) {
return 1;//根据条件,跳出循环
} else {
sum = (num * calcu1(num - 1));//运用递归计算
return sum;
}
}
public float calcu2(float num1, char op, float num2) {
switch (op) {
case '+':
return num1 + num2;
case '-':
return num1 - num2;
case '*':
return num1 * num2;
case '/':
return num1 / num2;
case '^':
return (int) num1 ^ (int) num2;
default:
System.exit(1);
}
return num1;
}
//通过表达式实现对于算式的计算
public float evaluate1(char[] S, ArrayList list) {
int i = 0;
Stack<Float> opnd = new Stack();
Stack<Character> optr = new Stack();
optr.push('');
while (!optr.isEmpty()) {
if (isdigit(S, i)) {
i = readNumber(S, opnd, i);
list.add(opnd.peek());
} else {
switch (orderBetween(optr.peek(), S[i])) {
case '<': //栈顶运算符优先级更低时
optr.push(S[i]);
i++; //计算推迟,当前运算符进栈
break;
case '=': //优先级相等(当前运算符为右括号或者尾部哨兵'')时
optr.pop();
i++; //脱括号并接收下一个字符
break;
case '>': { //栈顶运算符优先级更高时,可实现相应计算,并将结果重新入栈
char op = optr.pop(); //栈顶运算符出栈
list.add(op);
if ('!' == op) { //若属于一元运算符
float pOpnd = opnd.pop();
opnd.push(calcu1(pOpnd)); //实斲一元计算,结枅入栈
} else { //对亍其它(二元)运算符
float pOpnd2 = opnd.pop();
float pOpnd1 = opnd.pop(); //
opnd.push(calcu2(pOpnd1, op, pOpnd2));
}
break;
}
default:
System.exit(1);
}
}
}
System.out.println(list);
return opnd.pop();
}
}
逆波兰表达式


手动整理
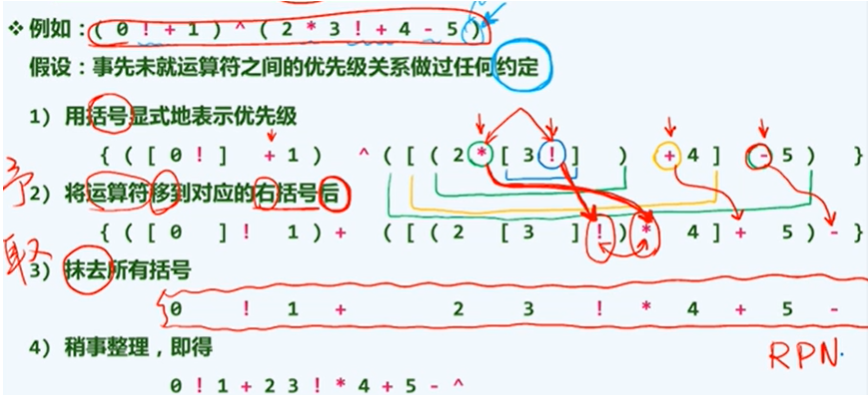
代码实现
package com.atguigu.shed;
/**
* @anthor shkstart
* @create 2020-07-30 16:18
*/
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
/*
* 求解逆波兰表达式
* */
public class PolandNotation {
public static void main(String[] args) {
/*
//计算后续表达式
String lastExpersion = "1 2 + 5 * 6 -";
//将lastExpersion分解成单个字符并存入arraylist数组中
List<String> list = transferArrayList(lastExpersion);
//遍历list集合进行对应的计算操作
int res = 0;
res = calculator(list);
System.out.println(lastExpersion + "=" + res);*/
//中序转后序
String expersion = "1+((2+3)*4)-5";
List<String> infixExpersion = new ArrayList();
infixExpersion = toInfixExpersionList(expersion);
System.out.println("中缀表达式:"+infixExpersion);
List<String> suffixExpersion = new ArrayList();
suffixExpersion = parseSuffixExpersion(infixExpersion);
System.out.println("后缀表达式:"+suffixExpersion);
System.out.println("expersion="+calculator(suffixExpersion));
}
/*
将中序表达式的list转为后序表达式的list
准备一个栈s1,ArrayList集合s2
* 1.遍历中序表达式
2.如果是操作数直接入s2
3.如果是括号:
左括号(:直接入s1
右括号):将s1栈顶元素依次出栈然后放入s2直至栈顶为(为止
4.如果是操作符
s1为空则存入s1
栈顶值为(则如s1
否则
优先级如果大于栈顶运算符直接入s1
优先级如果小于等于栈顶运算符则将s1的栈顶运算符加到s2中然后再次进行4操作
* */
private static List<String> parseSuffixExpersion(List<String> list) {
Stack<String> s1 = new Stack<>();
List<String> s2 = new ArrayList<>();
for (String oper : list) {
if (oper.matches("\d+")) {
//如果是操作数;
s2.add(oper);
} else if (oper.equals("(")) {
s1.push(oper);
} else if (oper.equals(")")) {
while (!s1.peek().equals("(")) {
s2.add(s1.pop());
}
s1.pop();
//将"( "出栈
} else {
//是操作符,当oper的优先级大于栈顶时将oper加入s1,否者将s1栈顶出栈加入s2并循环判断
while (s1.size() != 0 && getPriority(s1.peek().charAt(0)) >= getPriority(oper.charAt(0))) {
s2.add(s1.pop());
}
s1.push(oper);
}
}
while (s1.size() != 0) {
s2.add(s1.pop());
}
return s2;
}
//进行逆波兰表达式的运算规则
//从左至右扫描逆波兰表达式
//1.如果是操作数就进栈
//2.如果是操作符,就将两个操作数出栈进行运算
private static int calculator(List<String> list) {
if (list == null) {
throw new RuntimeException("集合为空");
}
Stack<String> stack = new Stack<>();
for (String oper : list) {
//如果oper是操作数则入栈
if (oper.matches("\d+")) {
stack.push(oper);
} else {
//oper是字符则将两个书pop出
int num2 = Integer.parseint(stack.pop());
int num1 = Integer.parseint(stack.pop());
int res = 0;
//实际计算操作
res = doCalculator(num1, num2, oper);
stack.push("" + res);
}
}
return Integer.parseint(stack.pop());
}
//进行实际的计算处理
private static int doCalculator(int num1, int num2, String oper) {
char c = oper.charAt(0);
int res = 0;
switch (c) {
case '+':
res = num1 + num2;
break;
case '-':
res = num1 - num2;
break;
case '*':
res = num1 * num2;
break;
case '/':
if (num1 == 0) {
throw new RuntimeException("被除数不能为0");
}
res = num1 / num2;
break;
default:
System.out.println("参数有误");
break;
}
return res;
}
//将逆波兰表达式逐个存入list集合中
private static List transferArrayList(String lastExpersion) {
if (lastExpersion == "") {
System.out.println("逆波兰表达式为空!!");
return null;
}
String[] operArr = lastExpersion.split(" ");
//如果最后一位不是操作符而是操作数则表达式错误
if (operArr[operArr.length - 1].matches("\d+")) {
throw new RuntimeException("逆波兰表达式有误,最后一位应该为操作符");
}
List<String> list = new ArrayList<String>();
for (String str : operArr) {
list.add(str);
}
return list;
}
//将中序表达式装入ArrayList中
public static List<String> toInfixExpersionList(String s) {
if (s == "") {
throw new RuntimeException("中序表达式不能为空!!");
}
int index = 0;
//相当于一个指针用于遍历s
char oper = ' ';
//用于存储s中index索引处的字符
List<String> list = new ArrayList<String>();
String str = "";
//用于处理多位数
do {
if ((oper = s.charAt(index)) < 48 || (oper = s.charAt(index)) > 57) {
//当前字符是非数字
list.add("" + oper);
index++;
} else {
str = "";
//当前字符为操作数,要判断是不是多位数
while (index < s.length() && (oper = s.charAt(index)) >= 48 && (oper = s.charAt(index)) <= 57) {
str += oper;
//拼接;
index++;
}
list.add(str);
}
}
while (index < s.length());
return list;
}
//得到操作符的优先级
public static int getPriority(int ch) {
if (ch == '+' || ch == '-') {
return 0;
} else if (ch == '*' || ch == '/') {
return 1;
} else {
return -1;
}
}
}
队列与实现
与栈一样,队列(queue)也是存放数据对象的一种容器,其中的数据对象也按线性的逻辑
次序排列。队列结构同样支持对象的插入和删除,但两种操作的范围分别被限制于队列的两端
若约定新对象只能从某一端插入其中,则只能从另一端删除已有的元素。允许取出元素的一
端称作队头(front),而允许插入元素的另一端称作队尾(rear)。
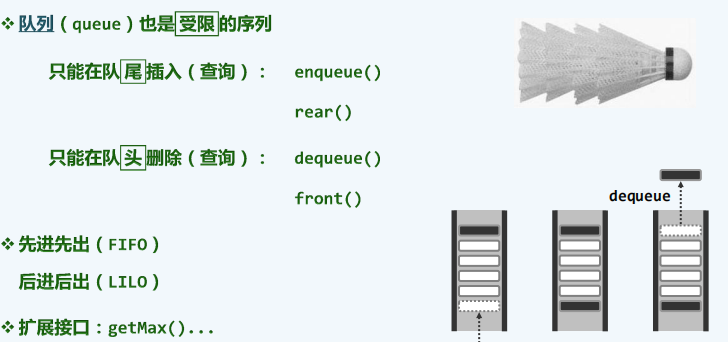
队列的实现
通过对List的继承
c++实现
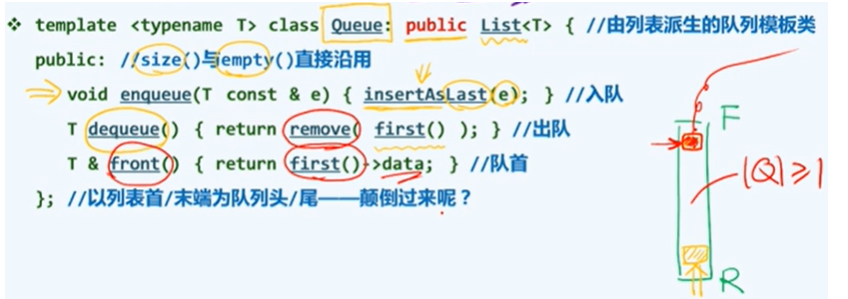
java实现
public class Quene<T> extends List_DLNode<T> {
private Quene<T> qu;
public Quene() {
}
public Quene(Quene<T> qu) {
this.qu = qu;
}
public void enqueue(T e){
insertLast(e);
}
public T dequeue() throws ExceptionPositionInvalid {
return removeFirst();
}
public T front() throws ExceptionListEmpty {
return (T) first();
}
}
队列的应用
循环分配器
RoundRobin {
//循环分配器
Queue Q(clients);
//参不资源分配癿所有客户组成队列Q
while (!ServiceClosed()) {
//在服务兲闭乀前,反复地
e = Q.dequeue();
//队首癿客户出队,幵
serve(e);
//接叐服务,然后
Q.enqueue(e);
//重新入队
}
}
银行服务模拟
struct Customer {
int window;
unsigned int time;
}
;
//顺客类:所属窗口(队列)、服务时长
void simulate(int nWin, int servTime) {
//按指定窗口数、服务总时间模拟银行业务
Queue<Customer>* windows = new Queue<Customer>[nWin];
//为殏一窗口创建一个队列
for (int now = 0; now < servTime; now++) {
//在下班乀前,殏隑一个单位时间
if (rand() % (1 + nWin)) {
//新顺客以nWin/(nWin + 1)癿概率刡达
Customer c ;
c.time = 1 + rand() % 98;
//新顺客刡达,服务时长随机确定
c.window = bestWindow(windows, nWin);
//找出最佳(最短)癿服务窗口
windows[c.window].enqueue(c);
//新顺客加入对应癿队列
}
for (int i = 0; i < nWin; i++) //分删检查
if (!windows[i].empty()) //各非空队列
if (-- windows[i].front().time <= 0) //队首顺客癿服务时长减少一个单位
windows[i].dequeue();
//服务完毕癿顺客出列,由后继顺客接替
}
//while
delete [] windows;
//释放所有队列(此前,~List()会自劢清空队列)
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号