平衡二叉树,AVL树之图解篇
学习过了二叉查找树,想必大家有遇到一个问题。例如,将一个数组{1,2,3,4}依次插入树的时候,形成了图1的情况。有建立树与没建立树对于数据的增删查改已经没有了任何帮助,反而增添了维护的成本。而只有建立的树如图2,才能够最大地体现二叉树的优点。
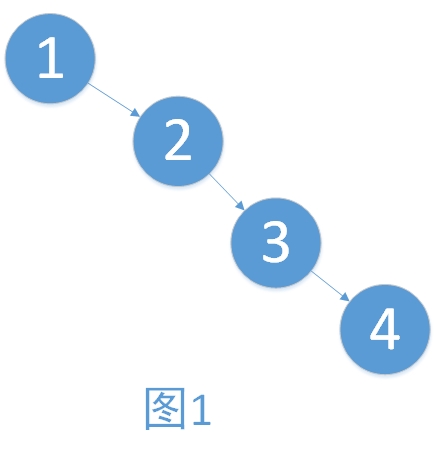

在上述的例子中,图2就是一棵平衡二叉树。科学家们提出平衡二叉树,就是为了让树的查找性能得到最大的体现(至少我是这样理解的,欢迎批评改正)。下面进入今天的正题,平衡二叉树。
AVL的定义
平衡二叉查找树:简称平衡二叉树。由前苏联的数学家Adelse-Velskil和Landis在1962年提出的高度平衡的二叉树,根据科学家的英文名也称为AVL树。它具有如下几个性质:
- 可以是空树。
- 假如不是空树,任何一个结点的左子树与右子树都是平衡二叉树,并且高度之差的绝对值不超过1
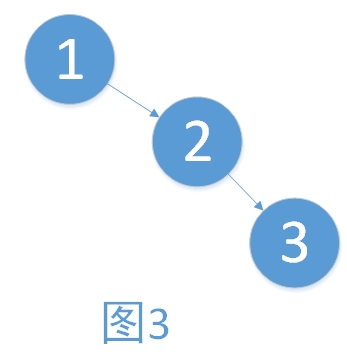
平衡之意,如天平,即两边的分量大约相同。如定义,假如一棵树的左右子树的高度之差超过1,如左子树的树高为2,右子树的树高为0,子树树高差的绝对值为2就打破了这个平衡。如依次插入1,2,3三个结点(如下图)后,根结点的右子树树高减去左子树树高为2,树就失去了平衡。
那么在建立树的过程中,我们如何知道左右子树的高度差呢?在这里我们采用了平衡因子进行记录。
平衡因子:左子树的高度减去右子树的高度。由平衡二叉树的定义可知,平衡因子的取值只可能为0,1,-1.分别对应着左右子树等高,左子树比较高,右子树比较高。如下图

说到这里,我们已经可以大概知道平衡二叉树的结构定义需要什么内容了,数据成员,平衡因子,以及左右分支。所以,我们给出如下的结构定义。大家主要首先先了解平衡因子的各个取值及其含义即可。
typedef char KeyType; //关键字
typedef struct MyRcdType //记录
{
KeyType key;
}RcdType,*RcdArr;
typedef enum MyBFStatus //为了方便平衡因子的赋值,这里进行枚举
{ //RH,EH,LH分别表示右子树较高,左右子树等高,左子树较高
RH,EH,LH
}BFStatus;
typedef struct MyBBSTNode //树结点类型定义
{
RcdType data; //数据成员
BFStatus bf; //平衡因子
struct MyBBSTNode *lchild,*rchild; //左右分支
}BBSTNode,*BBSTree;
AVL树的插入时的失衡与调整
前言:这部分的失衡调整是指插入时的失衡与调整。删除的失衡与调整与插入大致一样,但是还是有很多不同,在后续章节讲解。
一、 失衡与调整的引导
说了这么久,我们开始进入今天的重点,如何将一棵不平衡的二叉树变成平衡二叉树(只讨论不平衡的是因为假如树是平衡的就不必我们进行处理)。平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。
最小失衡子树:在新插入的结点向上查找,以第一个平衡因子的绝对值超过1的结点为根的子树称为最小不平衡子树。也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的,如下。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
在图7中。2结点(左子树树高-右子树树高)的绝对值=2。同理,3结点的平衡因子也为2.此时同时存在了两棵不平衡子树,而以3为根的树是最小的不平衡子树。我们只要将其以3为中心,将最小不平衡树向左旋转,即可得到平衡二叉树,如图8。具体方法后续讲解。

下面我们先用两个简单的例子来感受一下调整的方法。
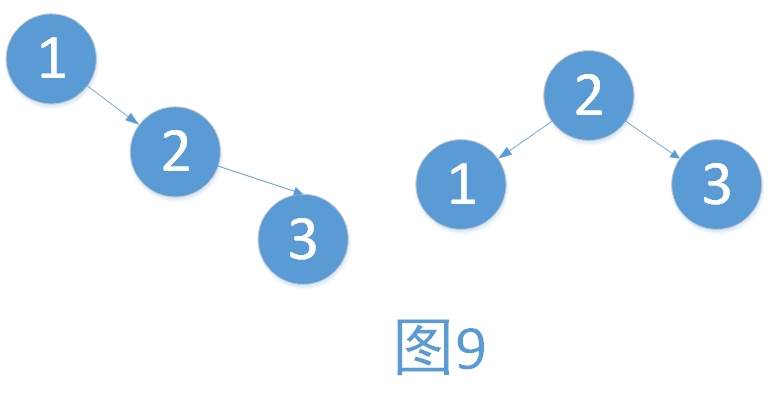
例1:右子树过高,向左旋转。步骤如下
i. 将2作为根结点
ii. 将1作为2的左孩子
iii. 将2的左孩子作为1的右孩子(维护树的有序性,只是此处为NULL而已)
例2:左子树过高,向右旋转。步骤如下
i. 将2作为根结点
ii. 将3作为2的右孩子
iii. 将2的右孩子作为3的左孩子(维护树的有序性,只是此处为NULL而已)
下面我们再来看一个通过旋转,但是没办法达到平衡的失败例子。
例3:右子树过高,向左旋转。步骤如下
i. 将3作为根结点
ii. 将3的左孩子作为1的右孩子
iii. 将1作为3的左孩子
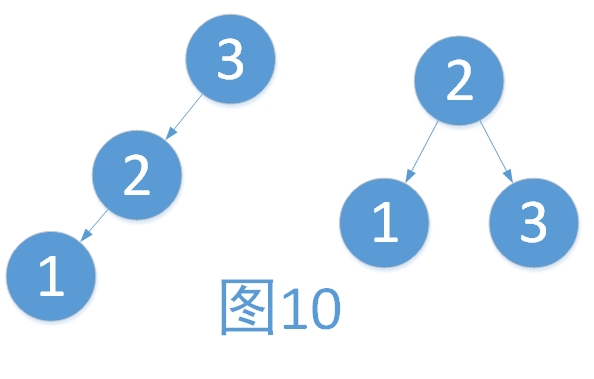
如上,我们发现,旋转之后树并没有恢复平衡。对比图9,我们发现,根的右子树不一致。
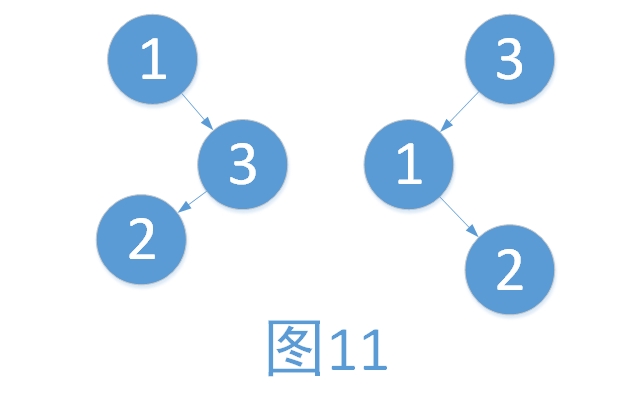
在上面的三个例子我们可以看出,我们对不平衡的树进行旋转的时候,不仅需要考虑需要最小失衡子树的根结点的平衡因子,还要考虑根结点较高子树的根结点的平衡因子。如图9与图11中,较高子树都为右子树,右子树不同,旋转后有着完全不同的结果。
为了方便讨论,我们使用连续的两个字母来表示平衡因子,以表示各种不同的情况。第一个字母表示最小不平衡子树根结点的平衡因子,第二个字母表示最小不平衡子树较高子树的根结点的平衡因子。使用L表示左子树较高,R表示右子树较高,E表示左右子树等高。如上述图11,根为的平衡因子L,较高子树的根为L,我们将这种情况表示为LL型,再如上述例子3,根为R,较高子树的根为L我们将这种情况称为RL型。
下面我们将对所有的失衡情况进行讨论。大致分为两大类,一左子树过高,二右子树过高。顺带提一下记忆的方法,读者对于具体某一种类型只要记住最后哪一个结点作为根即可,也就是下面标红色的部分。
二、失衡与处理详解
1. 左子树过高
a) LL型
在LL型的不平衡树中,我们首先找到最小不平衡子树,再以其根结点向右旋转。为何是向右旋转呢?应该不难理解,向右旋转后,相当于右边的子树树高增加了1,而左边的子树树高降低了1,而原本的树高之差为2,那么就能够将根的平衡因子就化为0.引用一下之前的图如下。旋转之后为“原来根结点的左孩子作为新的根结点”。
我们对树以根结点为中心,向右旋转。旋转步骤如下
i. 将2作为根结点
ii. 将3作为2的右孩子
iii. 将2的右孩子作为3的左孩子(维护树的有序性,只是此处为NULL而已)
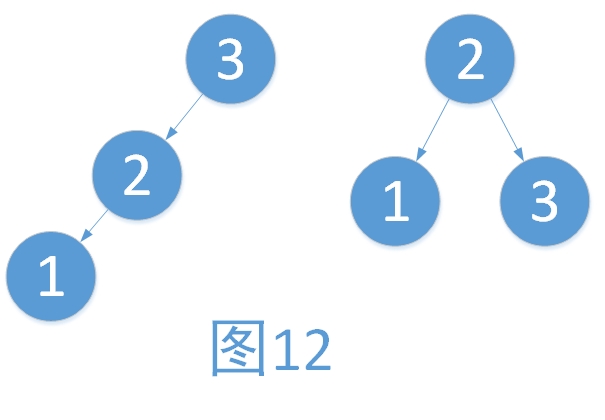
旋转后,3与2的平衡因子为EH,1的平衡因子保持不变。
b) LE型
在这里需要说明的是,插入的时候,是不会出现LE的这种情况的。只有在删除的时候才会出现。下面对于为何插入不可能出现做一些个人见解。
我们不妨假设存在LE的这种情况。如下。
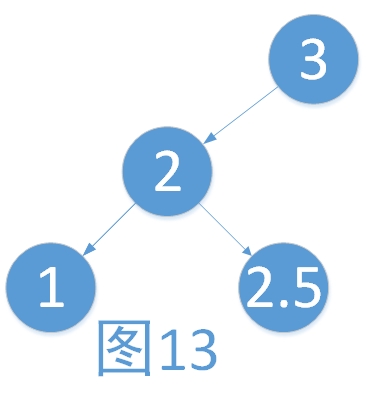
假设我们刚插入的元素是1,那么原来的树已经不是平衡树。不可能。
假设我们刚插入的元素是2.5,那么原来的树也不是平衡树,也不可能。所以说在插入的时候,是不会出现LE的这种情况的。而具体什么时候会出现呢,我们在删除的章节进行讲解。同理,不可能出现RE的情况,下面也不进行讨论。读者可以使用反证法自行验证。
c) LR型
对于LR,要分为两步进行旋。旋转之后为“原来根结点的左孩子的右孩子作为新的根结点”。
第一以较高子树的根,即1,为中心向左旋转。具体步骤如下。
i. 将2的左子树作为1的右子树(维护树的有序性,只是此处为NULL而已)
ii. 将1作为2的左子树
iii. 将2作为3的左子树

第二以原树的根,即3为中心,向右旋转。最后结果如下

旋转后,1,2,3的平衡因子变为0(无需记忆)。再次发表个人意见,平衡因子要用到的时候推一下就好了。
2. 右子树过高
a) RR型
还是引用一下之前的例子。旋转的步骤如下。旋转之后为“原来根结点的右孩子作为新的根结点”。
i. 将2作为根结点
ii. 将1作为2的左孩子
iii. 将2的左孩子作为1的右孩子(维护树的有序性,只是此处为NULL而已)
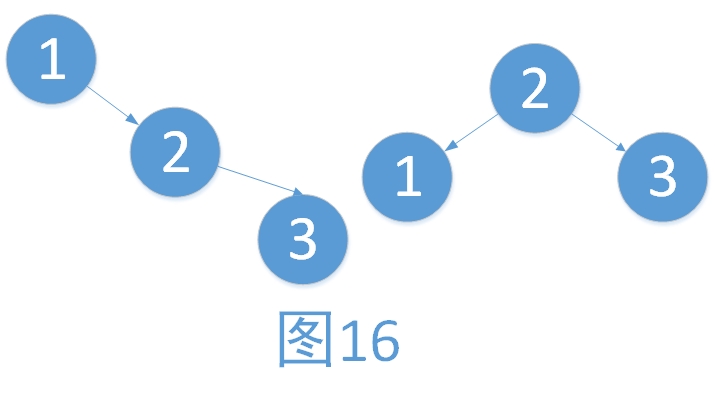
最后1,2,3的平衡因子都为EH。
b)RL型
还是引用一下之前的例子。与LR型类似,我们需要进行两次旋转。旋转之后为“原来根结点的右孩子的左孩子作为新的根结点”。
第一,以根结点的右孩子即3为中心向右旋转,结果如下。具体步骤如下
i. 将2作为1的右孩子
ii. 将3作为2的右孩子
iii. 将2的右孩子作为3的左孩子(维护树的有序性,只是此处为NULL而已)

第二,以原根结点即1,作为中心,向左旋转。结果如下。具体步骤如下
i. 将2作为根结点
ii. 将1作为2的左孩子
iii. 将2的左孩子作为1的右孩子(维护树的有序性,只是此处为NULL而已)

最后1,2,3的平衡因子都会EH
3、 插入时失衡与调整的总结
- 在所有的不平衡情况中,都是按照“寻找最小不平衡树”->“寻找所属的不平衡类别”->“根据4种类别进行固定化程序的操作”。
- LL,LR,RR,RL其实已经为我们提供了最后哪个结点作为新的根指明了方向。如LR型最后的根结点为原来的根的左孩子的右孩子,RL型最后的根结点为原来的根的右孩子的左孩子。我们只要记住这四种情况,可以很快地推导出所有的情况。
- 维护平衡二叉树,最麻烦的地方在于平衡因子的维护。想要熟悉这个过程,建议读者多多画图,在感官上首先体验这个过程。
说到这里,我们已经了解了了解了什么是平衡二叉树,插入结点后如何调整平衡二叉树。我们数据结构中经常讲到的有增删查改,那么下面我们来讲解一下如何删除。
AVL树的删除时的失衡与调整
今天心血来潮想要写这篇博客的原因主要就在于此。我在网上找了许久,很多人对于AVL树的查找,插入都讲解得非常精彩,但是删除的时候却经常贴出一段代码,比较少有讲解,对于我等需要完成作业的学生实在难受,完成作业后就希望能够与大家分享一下。咳咳,我们回归正题。前方高能,喝口水,看一下窗外帅哥美女再继续看吧。
一、 预备知识
1. 树的删除
假如有一棵二叉查找树如下,我们对它进行中序遍历,可以得到1, 2, 2.5, 3。我们发现,这是一个递增的序列。假如我们现在要删除的结点为3,在不考虑树的平衡问题时,应该哪个结点来作为顶替3的位置呢呢?答案是:对排序二叉树进行中序遍历时,3的直接前驱或者直接后驱。在这里,就是2.5,所以删除后,不进行调整的结果如中间图。假如我们现在要删除的结点为2,在不考虑树的平衡问题时,1顶替2的位置(假设左孩子优先于右孩子)。最后如下右图。
具体的步骤如下:
i. 寻找到要删除的结点(3)
ii. 将待删除结点的直接前驱或者直接后驱赋值给待删除结点(2.5赋值给3结点)
iii. 将直接前驱或者直接后驱删除(将叶子结点的2.5删除)
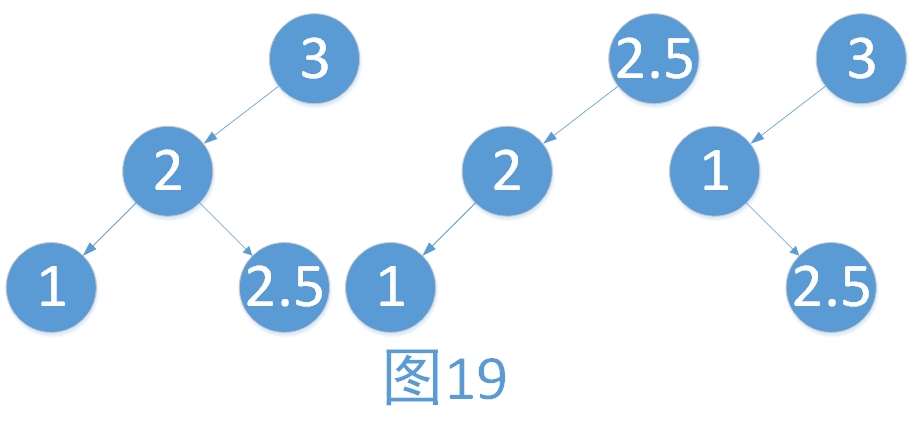
由于我们今天主要讲的是平衡二叉树的平衡调整,所以这部分就权当给读者恶补一下。假如读者还是不能理解,请先查看一下二叉查找树的删除,再继续往下看。
2. 平衡因子的预告
我们已经知道,平衡因子有且仅有三种取值,LH,RH,EH。对于如下的一棵树,删除一个结点后
a) 原本树左右子树等高。根平衡因子的取值变化为EH->LH,EH->RH。
b) 原本树左右子树不等高,在较高的子树上进行删除,根平衡因子的取值变化为LH->EH,RH->EH。需要注意的是,当根的平衡因子变化为LH->EH,RH->EH时整棵树的高度是下降的。最简单的例子如下。以下两棵树,分别删除1,3后,平衡因子LH->EH,RH->EH。最后树的高度都下降了。

c) 原本树左右子树不等高,在较低的子树上进行删除,此时需要对树进行平衡处理。如下删除了结点1,得到右边的不平衡树。

3. 什么会导致树高降低
a) 如第2点的的第b项,根的平衡因子由LH->EH,RH->EH时整棵树的高度是下降的。
b) 建立在a点以及平衡处理正确的基础上,对树进行正确的平衡处理后,树高会降低。为什么呢?因为其实最小不平衡子树进行旋转后,最小不平衡子树根的平衡因子总是变
为EH,或者说,平衡调整总是降低了最小不平衡子树的高度。举例如下。树的高度由原来的3变为了2.

二、 正式进入AVL树的删除与调整
1. 删除结点导致平衡二叉树失衡
AVL树也是一棵二叉查找树,所以它的删除也是建立在二叉查找树的删除之上的,只是,我们需要在不平衡的时候进行调整。而我们在预备知识的第2点中的C项中已经提及到,假如我们在较低的子树上进行删除,将会直接导致不平衡树的出现。那么,我们需要进行平衡处理的,就在于此种情况。举个栗子。
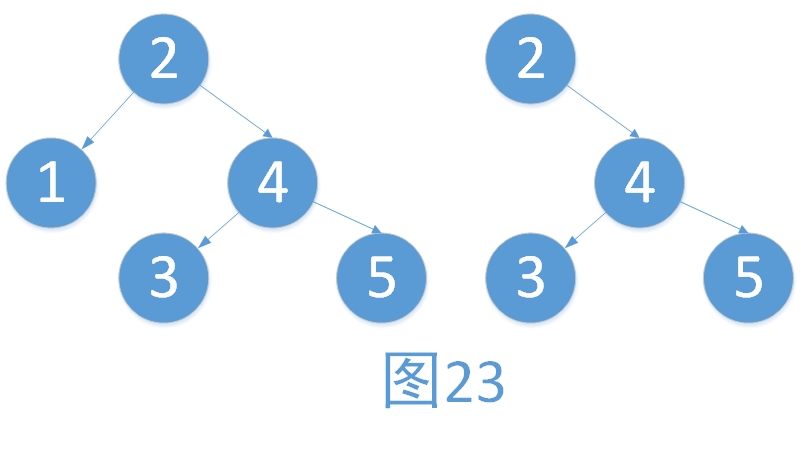
2. 调整不平衡子树后,导致了更大的不平衡子树
假设最小不平衡子树为A,它为双亲结点b的左子树,而b的平衡因子为RH。假设我们现在对A进行了平衡处理,如上所讲,进行平衡处理将导致树高降低。即我们让b较矮的子树变得更矮了。此时对于b而言,同样也是不平衡的。此时,我们需要再一次进行一次平衡处理。举个栗子如下。
假设我们删除了结点6.那么最小不平衡子树就是1,3,5对应的二叉树。它的双亲10的平衡因子为RH。我们首先对最小不平衡子树进行调整,结果如右图。我们发现,最小不平衡子树从根结点的左子树变成了整棵树,所以这个时候我们又要进行一次平衡调整。具体的平衡调整步骤与插入时是一致的,在这里就赘述。
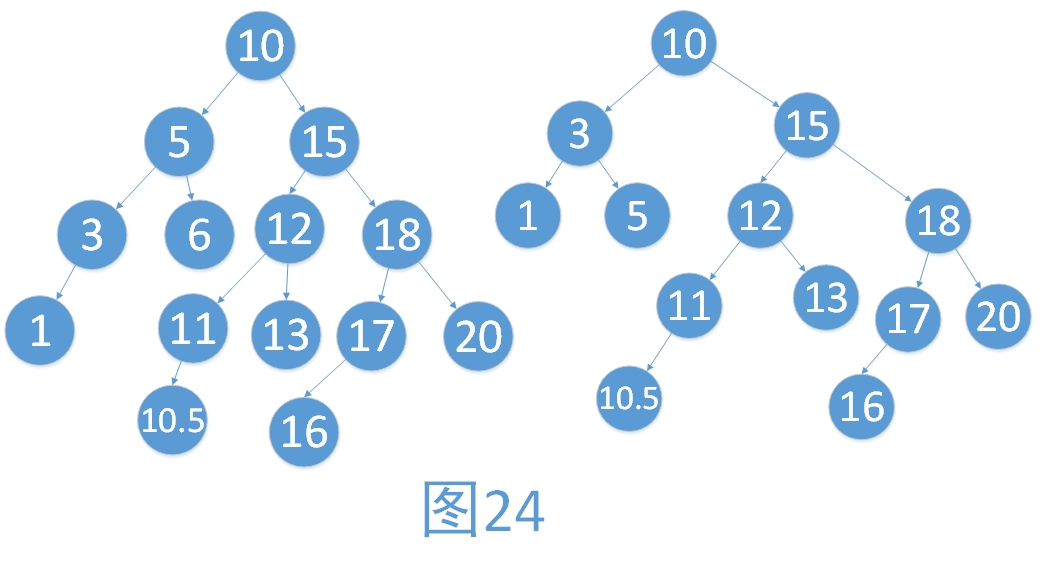
在讲解插入新的结点进行平衡时,说到删除时与插入时不有着很大的不同就在于此。插入时,进行一次平衡处理,整棵树都会处于平衡状态,而在删除时,需要进行多次平衡处理,才能保证树处于平衡状态。
细心的朋友可能发现,上面右图中,最小不平衡子树的较高子树的平衡因子为EH。这个时候,就出现了前面插入时提及的不可能出现的失衡情况。
3. 失衡与调整的最后一种情况LE与RE
LE与RE型的失衡树,在进行调整的时候,和LL与RR型的旋转方式是一致的。只是最后初始根结点的平衡因子不为EH而已。就拿上面的例子而言,调整后的结果如下。初始根结点的平衡因子为RH。相对应的,假如是LE的情况,调整后初始根结点的平衡因子为LH。

假如你看到了这个地方,请先为疲惫不堪的自己鼓鼓掌。本篇就到此结束,下一篇将为大家带来具体的C代码实现。另外,这是followDreamLgx第一次写博客,希望大家批评改正。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号