动态规划—背包问题

就在这几天，我看到了一个动态规划的典型题目:

这个题目是动态规划的典型题目——背包问题。其实这个问题十分简单，就是有一个背包，有价值不同，重量不一的物品。问题就是如何将价值最大的物品放满背包且重量刚好。

如图所示：

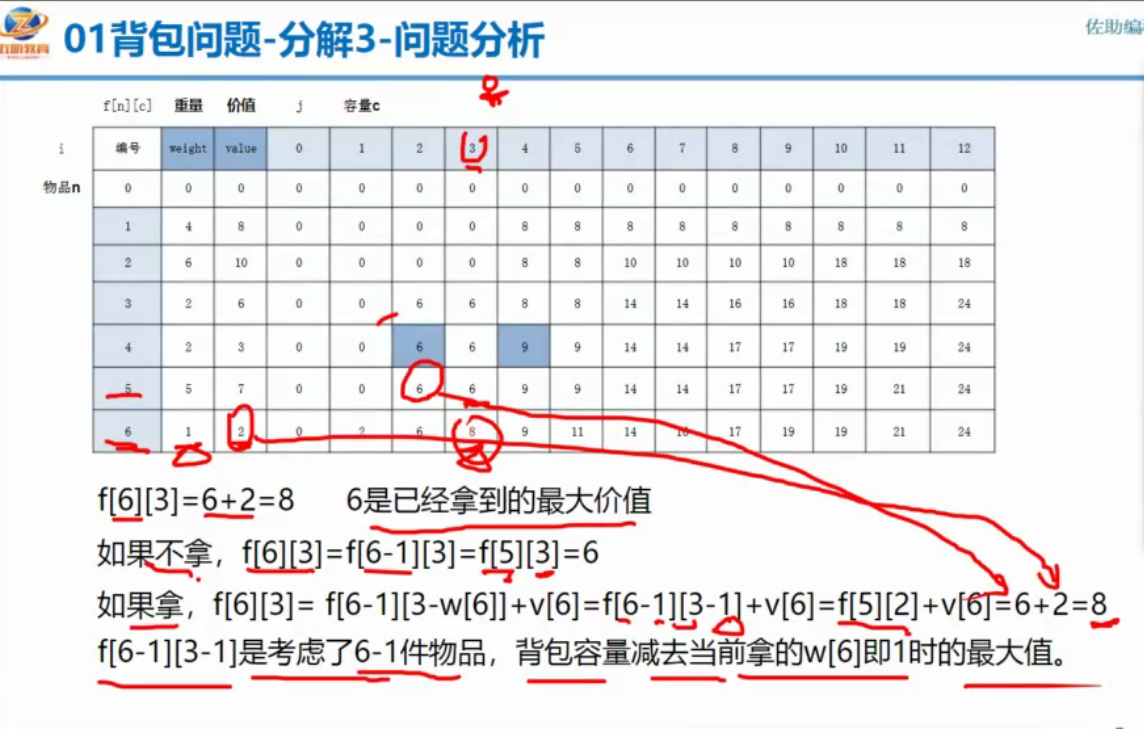
所以这个问题的程序的状态转移方程是这样的：

1 if(j<w[i])//背包装不下的时候,f为上一个值。
2 {
3           f[i][j]=f[i-1][j];
4 }
5 else//否则（如果可以拿），使用状态转移方程
6 {
7           f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
8 }

完整的程序是这样的：

#include <bits/stdc++.h>
using namespace std;
int f[15][15];

int main()
{
    cout<<"容量";
    for(int i=1;i<=12;i++)
    {
        cout<<i<<setw(5);
    }
    cout<<endl;
    cout<<"-------------------------------------------------------------------"<<endl;//显得更直观 
    int v[]={0, 8, 10, 6, 3, 7, 2}; //设定化物品价值数组
    int w[]={0, 4, 6, 2, 2, 5, 1}; //设定化物品重量数组
    int n=6,c=12; //设定物品数量与背包容量
    memset(f,0,sizeof(f));//初始化f
    for(int i=1;i<=n;i++)//循环列举每一个物品 
    {
        for(int j=1;j<=c;j++)
        {
            if(j<w[i])//背包装不下的时候,f为上一个值。
            {
                f[i][j]=f[i-1][j];
            }
            else//否则（如果可以拿），使用状态转移方程
            {
                f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
            }
        }
    }
    for(int i=1;i<=n;i++)//输出结果
    {
        for(int j=1;j<=c;j++)
        {
            cout<<setw(5)<<f[i][j];
        }
        cout<<endl;
    }
    return 0; 
}