1、下面来通过这一道题 回顾回顾图这一张的相关内容
7-1 列出连通集 (30 分)
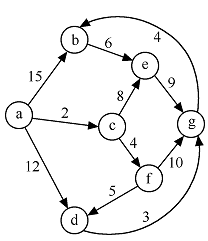
给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N-1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。
输入格式:
输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间用1空格分隔。
输出格式:
按照"{ v
1
v
2
... v
k
}"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
作者: 陈越
单位: 浙江大学
时间限制: 400 ms
内存限制: 64 MB
一开始,我想的是用邻接矩阵来写这一道题。

#include<iostream> using namespace std; #define MVNum 11 bool visited[MVNum] = {false}; #include<queue> typedef struct ArcNode{ // 边 int adjvex; //该边指向的顶点的位置 struct ArcNode *nextarc; //指向下一条边的指针 ??? }ArcNode; typedef struct VNode{ // 顶点 int data; //顶点的序号 ArcNode *firstarc; //指向第一条依附于该顶点的边的指针 }VNode,AdjList[MVNum]; typedef struct{ // 图 AdjList vertices; //存储顶点的数组 int vexnum,arcnum; //该图所包含的顶点数和边数 }ALGraph; void CreateUDG(ALGraph &G) { //采用邻接表表示法,创建无向图G cin>>G.vexnum>>G.arcnum; //输入顶点数边数 for(int i=0; i<G.vexnum; ++i) { //输入各点,构造表头结点表 G.vertices[i].data = i; //各顶点值就是对应的i值 G.vertices[i].firstarc = NULL; //初始化表头结点的指针域为NULL } for(int k=0; k<G.arcnum; ++k) { //输入各边两端的顶点,构造邻接表 int v1,v2; cin >> v1 >> v2 ; //输入边的两个顶点 ArcNode *p1 = new ArcNode; //生成一个新的边结点*p p1->adjvex=v2; //邻接点序号为v2 //头插法插入到G.vertices[v1].firstarc指向的结点之前 p1->nextarc=G.vertices[v1].firstarc; G.vertices[v1].firstarc = p1; ArcNode *p2 = new ArcNode; //生成一个新的边结点*p p2->adjvex=v1; //邻接点序号为v1 //头插法插入到G.vertices[v2].firstarc指向的结点之前 p2->nextarc=G.vertices[v2].firstarc; G.vertices[v2].firstarc = p2; } } int FirstAdjVex(ALGraph G, int v)//返回顶点v的第一个邻接点序号 { ArcNode *p=G.vertices[v].firstarc; if(p) return p->adjvex; else return -1; } int NextAdjVex(ALGraph G, int v, int w)//返回顶点v的相对于w的下一个邻接点序号 { ArcNode* p=G.vertices[v].firstarc; while(p) { if(p->adjvex==w) break; p=p->nextarc; } if(p->adjvex!=w || !p->nextarc)//如果没找到w或者w是最后一个邻接点 return -1; return p->nextarc->adjvex; } void DFS(ALGraph G, int v){ cout<<' '<<v<<' '; visited[v] = true; for(int w = FirstAdjVex(G , v);w>=0;w = NextAdjVex(G,v,w)){ if(!visited[w]){ DFS(G , w); } } } void DFSTraverse(ALGraph G){ for(int v = 0;v<G.vexnum ; ++v){ visited[v] = false; } // 访问标志数组的初始化 for(int v = 0;v<G.vexnum ; ++v){ if(!visited[v]){ cout<<"{"; DFS(G , v); cout<<"}"<<endl; } } } void BFS(ALGraph G , int v){ queue<int> q; visited[v] = true; cout<<' '<<v<<' '; q.push(v); while(!q.empty()){ int u = q.front(); q.pop(); for(int w = FirstAdjVex(G,u);w>=0;w = NextAdjVex(G, u , w)){ if(!visited[w]){ cout<<' '<<w<<' '; visited[w] = true; q.push(w); } } } } void BFSTraverse(ALGraph G){ for(int v = 0;v<G.vexnum ; ++v){ visited[v] = false; } // 访问标志数组的初始化 for(int v = 0;v<G.vexnum ; ++v){ if(!visited[v]){ cout<<"{"; BFS(G , v); cout<<"}"<<endl; } } } int main(){ ALGraph G; CreateUDG(G); DFSTraverse(G); BFSTraverse(G); return 0; }
可是结果却与答案有略微差别。
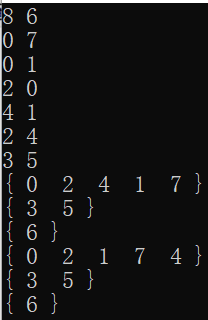
仔细比对后发现是1、2的顺序颠倒了。为什么会这样呢?实际上无论是进行DFS还是BFS时都可能不止有一种结果。以深搜为例,到“依次检查v的所有邻接点”这一步时,如果没有特殊规定的话,可允许有多种遍历邻接点的顺序,广搜亦如是。
但是,仔细读题可发现题目有这样的具体要求:“进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。”意思是题目已经默认像这样的情况我们优先遍历编号小的顶点。
而对于邻接表,这个操作就很难实现。要从小到大排序,数组肯定要比链表来得容易啊!纵观命题者意图,貌似暗示我们用邻接矩阵。于是我决定不再纠结,另起炉灶使用邻接矩阵!
写邻接矩阵很顺利,因为相对而言比邻接表更简单。等我写完之后跑起来,却发现几乎读不进数据,总是出现一些稀奇古怪的结果。经过多次仔细检查发现原来是我没有使用&把AMGraph传到函数内部。

#include<iostream> using namespace std; #define MVNum 10 #include<queue> bool visited[MVNum]; typedef struct{ int vexs[MVNum]; // 一位数组 存放顶点 int arcs[MVNum][MVNum]; // 二维数组 邻接矩阵 int vexnum,arcnum; // 当前图的顶点数、边数 }AMGraph; void CreateGraph(AMGraph &G){ // 如何将输入的信息->无向图 cin>>G.vexnum>>G.arcnum; // 依次输入顶点数目和边的数目 for(int i = 0 ; i < G.vexnum ; i++){ G.vexs[i] = i; } // 在本题中点的编号就是其序号 for(int m = 0 ; m < G.vexnum ; m++) for(int n = 0 ; n< G.vexnum ; n++) G.arcs[m][n] = 0; // 邻接矩阵初始化 for(int k = 0 ; k <G.arcnum ; k++){ int v1,v2; cin>>v1>>v2; // v1、v2分别是一条边两个顶点的端点 G.arcs[v1][v2] =1; G.arcs[v2][v1] =1; } // 两点之间有边:将值改为1进行标记 } void DFS(AMGraph &G , int v){ cout<<v<<' '; visited[v] = true; for(int w = 0 ; w < G.vexnum ; w++) if((G.arcs[v][w] == 1)&&(!visited[w])) DFS(G,w); } void DFSTraverse(AMGraph &G){ for(int v = 0 ; v <G.vexnum ; v++) visited[v] = false; // 初始化visited数组 一旦访问将其置为true for(int v = 0 ; v <G.vexnum ; v++){ if(!visited[v]){ cout<<"{"<<' '; DFS(G,v); cout<<"}"<<endl;} } } int FirstAdjVex(AMGraph &G , int u){ for(int i = 0 ;i<G.vexnum ; i++){ if(G.arcs[u][i] == 1){ return i; } } return -1; } int NextAdjVex(AMGraph &G ,int u , int w){ for(int i = w+1; i<G.vexnum; i++){ if(G.arcs[u][i] == 1){ return i; } } return -1; } void BFS(AMGraph &G , int v){ queue<int> q; visited[v] = true; cout<<v<<' '; q.push(v); while(!q.empty()){ int u = q.front(); q.pop(); for(int w = FirstAdjVex(G,u) ; w >= 0 ; w = NextAdjVex(G, u , w)){ if(!visited[w]){ cout<<w<<' '; visited[w] = true; q.push(w); } } } } void BFSTraverse(AMGraph &G){ for(int v = 0 ; v <G.vexnum ; v++){ visited[v] = false; } for(int v = 0 ; v<G.vexnum ; ++v){ if(!visited[v]){ cout<<"{"<<' '; BFS(G,v); cout<<"}"<<endl; } } } int main(){ AMGraph G; CreateGraph(G); DFSTraverse(G); BFSTraverse(G); return 0; }
这一下终于顺利通过了!但是和同学交流之后发现还可以更优化,代码更清晰简洁:

#include <iostream> #include <cstring> #include <queue> using namespace std; int n,m,v[11],Map[11][11]; void DFS(int x) { cout<<' '<<x; for(int i=0; i<n; i++) { if(!v[i]&&Map[x][i]==1) { v[i]=1; DFS(i); } } } void BFS(int x) { int y; queue<int>Q; Q.push(x); while(!Q.empty()) { y=Q.front(); cout<<' '<<y; Q.pop(); for(int i=0; i<n; i++) { if(!v[i]&&Map[y][i]==1) { v[i]=1; Q.push(i); } } } } int main() { int x,y; cin>>n>>m; memset(Map,0,sizeof(Map)); memset(v,0,sizeof(v)); while(m--) { cin>>x>>y; Map[x][y]=Map[y][x]=1; } for(int i=0; i<n; i++) { if(v[i]==0) { v[i]=1; cout<<"{"; DFS(i); cout<<" }"<<endl; } } memset(v,0,sizeof(v)); for(int i=0; i<n; i++) { if(v[i]==0) { v[i]=1; cout<<"{"; BFS(i); cout<<" }"<<endl; } } return 0; }
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
5.19更新
深入理解迪杰特斯拉算法
老师布置的作业题里面有一道要求用迪杰特斯拉算法求最短路径。我看了一遍课本,但还是有一点云里雾里,最后在网上看到了一篇文章,感觉写的很清晰,让我理解起来也很容易。下面来简单总结一下:
1、相关概念:
迪杰特斯拉算法是干什么的:用于对有权图进行搜索,找出图中两点的最短距离。
两个集合:
S:已求出最短路径的顶点集合。初始条件为一个源点。
U:未确定最短路径的顶点集合。
操作步骤:按最短路径长度的递增次序依次把U组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
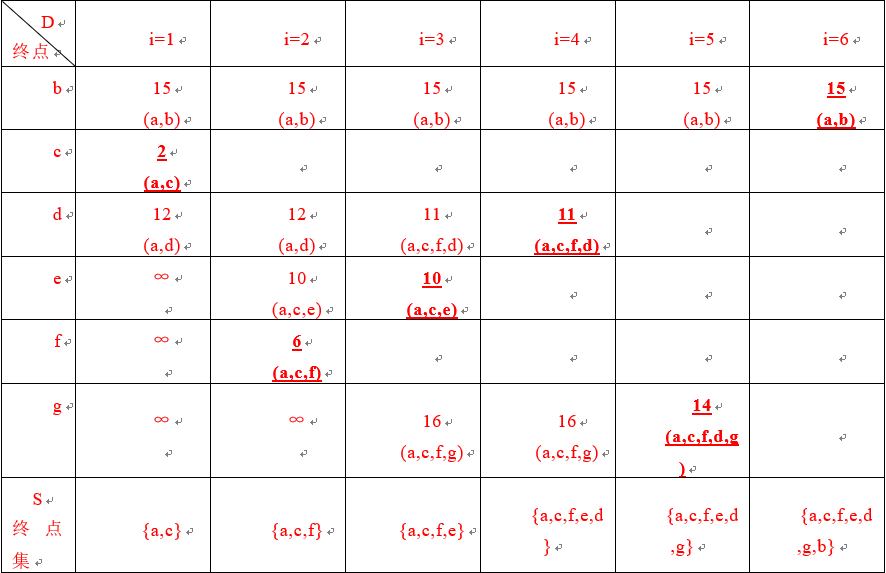
2、用例子理解
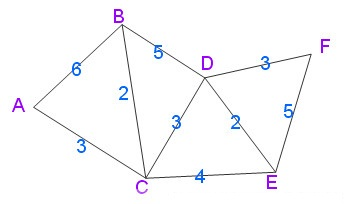
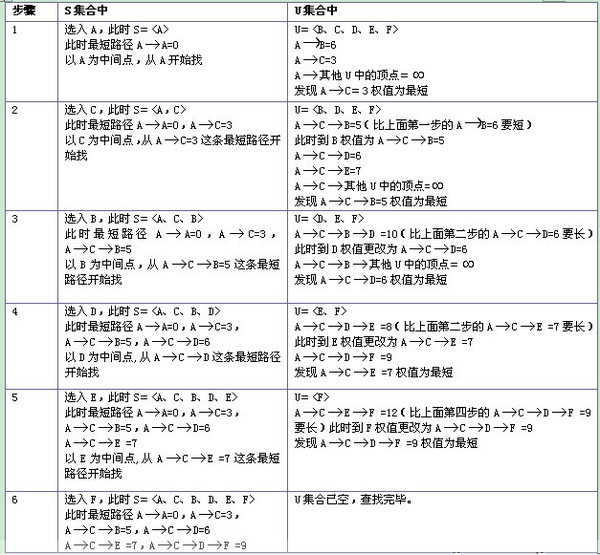
3、填表: