数据结构之线性表
线性表的抽象数据类型定义:
Date
线性表的数据对象集合为{A1, A2, ..., AN},每个元素的类型均为DateType 。其中除了第一个元素A1外,每一个元素有且只有一个直接前驱,除了最后一个元素AN外,每一个元素有且只有一个直接后继。数据元素之间的关系是一对一的关系。
operation
InitList(* L);//初始化操作,建立一个空的线性表
ListEmpty(L);//若线性表为空,返回true,否则返回false
ClearList(*L);//将线性表清空
GetElem(L, i, *e);//将线性表L中的第i个位置元素返回给e
LocateElem(L, e);//将线性表L中查找与给定值e相等的元素,如果查找成功返回该元素在表中序号表示;否则返回0表示失败
ListInsert(*L, i, e);//在线性表L的第i个位置插入新元素e
ListDelete(*L, i, *e);//删除线性表L中第i个元素,并用e返回其值
ListLength(L);//返回线性表L中元素的个素
endADT线性表的顺序存储结构
代码示例:
#include<stdio.h>
#define MAXSIZE 20 //存储空间初始化分配量
#define OK 1
#define ERROR 0
typedef int Status; //函数类型,返回OK, ERROR结果状态码
typedef int ElemType; //ElemType类型根据实际情况而定, 这里为int
typedef struct Person
{
ElemType date[MAXSIZE]; //int类型数组,存储数据元素
int length = -1; //线性表当前长度
}SqList;
Status GetElem(SqList L, int i, ElemType* e) //获得元素操作
{
if (i < 0 || i >= L.length || L.length == 0)
{
return ERROR;
}
*e = L.date[i];
return OK;
}
Status ListInsert(SqList* L, int i, ElemType e) //插入元素操作
{
if (L->length == MAXSIZE)
{
return ERROR;
}
if (i < 0 || i >= MAXSIZE)
{
return ERROR;
}
if (i < L->length ) //插入数据不在表尾
{
for (int k = L->length; k >= i; k--)
{
L->date[k + 1] = L->date[k];
}
}
else
{
L->date[i] = e;
}
L->date[i] = e;
L->length++;
return OK;
}
Status Pint_List(SqList* L) //输出线性表
{
int k = 0;
for (int i = 0; i <= L->length; i++)
{
k = 1;
printf("%d ", L->date[i]);
}
if (k == 1)
return OK;
else
return ERROR;
}
Status ListDelete(SqList* L, int i, ElemType* e) //删除线性表第 i 个元素
{
if (L->length == -1)
return ERROR;
if (i < 0 || i > L->length)
return ERROR;
*e = L->date[i];
if (i < L->length - 1) //如果删除不是线性表最后位置
{
for (int k = i; k < L->length ; k++)
{
L->date[k] = L->date[k + 1];
}
}
L->length--;
return OK;
}
int main()
{
SqList list1;
for (int i = 0; i < 10; i++)
{
int insert_signal = ListInsert(&list1, i, i);//接受插入信号
if (insert_signal == OK)
{
printf("%d 插入成功!\n",i);
}
else
{
printf("%d 插入失败!\n", i);
}
}
ListInsert(&list1, 10, 10);
ListInsert(&list1, 9, 10);
ListInsert(&list1, 1, 33);
int print_signal = Pint_List(&list1);//接受输出信号
if (print_signal == OK)
{
printf("输出成功!\n\n");
}
else
{
printf("输出失败!\n\n");
}
int temp_nal;
int delete_signal = ListDelete(&list1,1, &temp_nal);
if (delete_signal == OK)
{
printf("成功删除:%d\n\n", temp_nal);
print_signal = Pint_List(&list1);
}
else
{
printf("删除失败!\n\n");
}
return 0;
}优点:
- 无须为表示表中元素之间的逻辑关系而增加额外的存储空间
- 可以快速的存取表中任一位置的元素
缺点:
- 插入和删除操作需要移动大量元素
- 当线性表长度变化较大时,难以确定存储空间的容量
- 造成存储空间的“碎片”
线性表的链式存储结构
代码示例:
#include<stdio.h>
#include<stdlib.h>
int num = 0;
typedef struct Node
{
int value;
struct Node *next;
}std;
std *create_list() //创建一张空表
{
std* head = NULL;
return head;
}
std* Insert_list(std* head, int i, int elem)//插入操作
{
std* p1 = NULL, *p2 = NULL ,* p3 = NULL;
if (head == NULL) //判断链表是否为空
{
p2 = (std*)(malloc(sizeof(std)));
num++;
p2->value = elem;
p2->next = NULL;
head = p2;
return head;
}
if (i == 0 && head != NULL) //头插
{
p2 = (std*)(malloc(sizeof(std)));
num++;
p2->value = elem;
p2->next = head;
head = p2;
return head;
}
int j = 0;
p1 = head;
while (j < i && p1 != NULL)
{
p3 = p1;
p1 = p1->next;
j++;
}
if (p1 == NULL) //尾插
{
p2 = (std*)(malloc(sizeof(std)));
num++;
p2->value = elem;
p3->next = p2;
p2->next = NULL;
return head;
}
else //中插
{
p2 = (std*)(malloc(sizeof(std)));
num++;
p2->value = elem;
p3->next = p2;
p2->next = p1;
return head;
}
}
std* Deletelist(std* L, int i, int* e)//删除操作
{
int j = 0;
std* p = L;
std *p1 = NULL;
if (i == 0)//头删
{
L = p->next;
num--;
free(p);
return L;
}
while (j < i && p)
{
p1 = p;
p = p->next;
j++;
}
if (p->next == NULL)//尾删
{
p1->next = NULL;
num--;
return L;
}
else
{
p1->next = p->next;//中删
num--;
}
free(p);
return L;
}
std* modifylist(std* L, int i, int e)//修改操作
{
std* p = L;
int j = 0;
while (j < i && p)
{
p = p->next;
j++;
}
p->value = e;
return L;
}
void queryelem(std* L, int elem)//查找操作
{
std* p = L;
while (p)
{
if (p->value == elem)
{
printf("找到此元素:%d", elem);
return 0;
}
p = p->next;
}
printf("表中无此元素!");
}
void print_list(std* head)//打印链表
{
if (head)
{
std* p = head;
while (p)
{
printf("%d ", p->value);
p = p->next;
}
printf("\n");
}
else
{
printf("链表为空!");
}
}
int main()
{
std* head = create_list();
head = Insert_list(head, 0, 0);
head = Insert_list(head, 1, 1);
head = Insert_list(head, 2, 2);
head = Insert_list(head, 3, 3);
head = Insert_list(head, 4, 4);
head = Insert_list(head, 5, 5);
head = Insert_list(head, 6, 6);
int a;
print_list(head);
printf("删除第一个元素:\n");
head = Deletelist(head, 0, &a);
print_list(head);
printf("删除第三个元素:\n");
head = Deletelist(head, 3, &a);
print_list(head);
printf("删除最后一个元素:\n");
head = Deletelist(head, 4, &a);
print_list(head);
printf("修改第3个元素值为2\n");
head = modifylist(head, 3, 2);
print_list(head);
printf("查找是否存在值为3的结点!\n");
queryelem(head, 3);
return 0;
}优点:
- 单链表在找出位置的指针后,插入和删除的时间复杂度仅为O(1)
- 单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制
缺点:
单链表查找时间复杂度O(n)
循环链表
定义:
将单链表中终端结点的指针由空指针指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为循环链表
双向链表
定义:
双向链表是在单链表的每一个结点中,在设置一个指向前驱结点的指针域
存储结构
typedef struct Node
{
int value;
struct Node* prior;
struct Node *next;
}std;
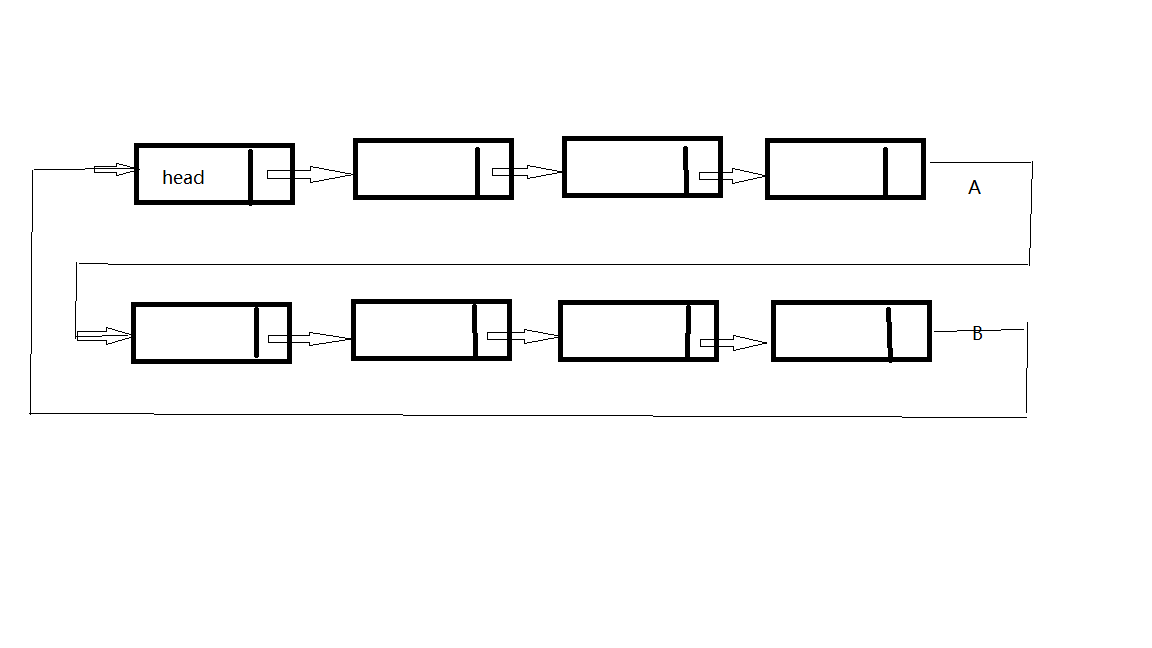 循环链表
循环链表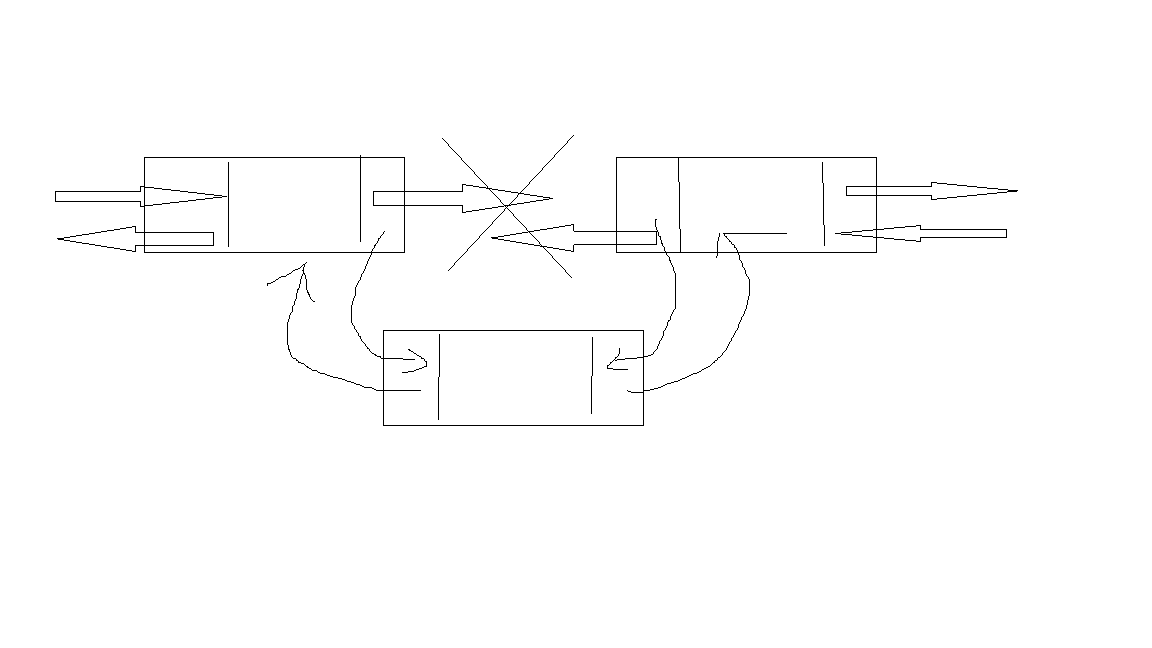 双向插入
双向插入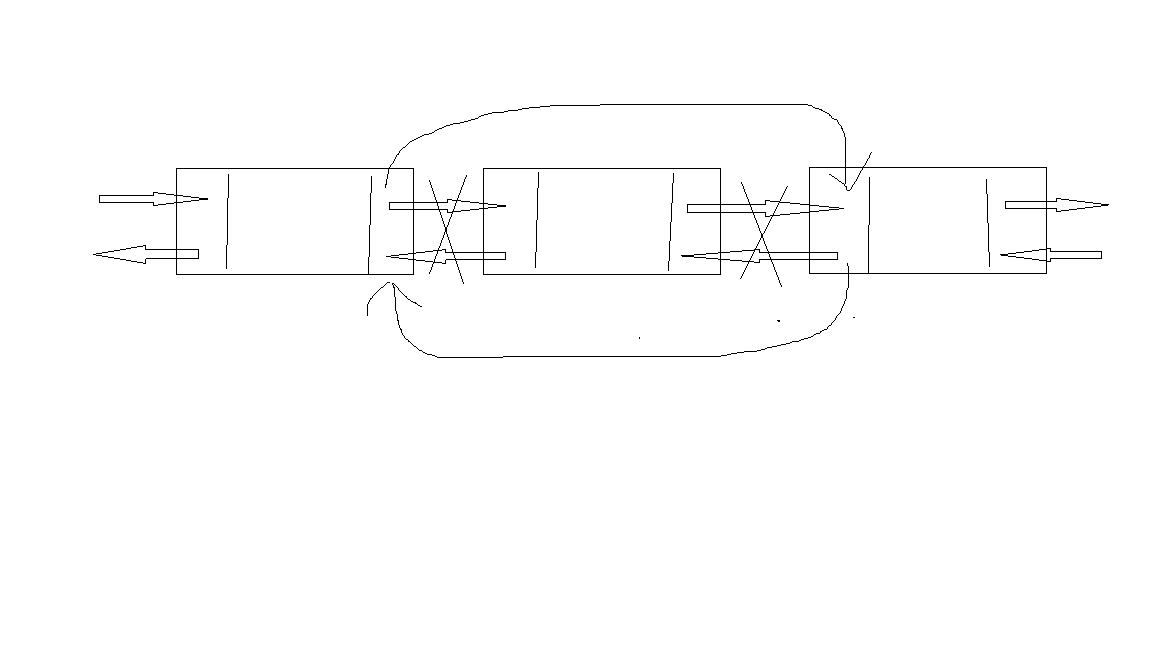 双向删除
双向删除
 浙公网安备 33010602011771号
浙公网安备 33010602011771号