DS博客作业02--栈和队列

| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业02--栈和队列 |
| 这个作业的目标 | 学习栈和队列的结构设计及运算操作 |
| 姓名 | 黄抒鸿 |

0.PTA得分截图

1.本周学习总结

1.1 栈

1.1.1画一个栈的图形：

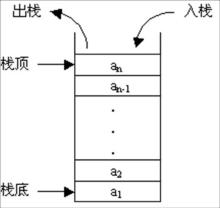
栈--又称“后进先出”的线性表。
栈顶（TOP）--允许插入和删除的一端。
栈底（bottom）--不允许插入和删除的一端。
空栈--表中没有元素。

栈中元素的特性：

具有线性关系；后进先出。

栈的进栈出栈规则：

栈顶出栈->栈底最后出栈；
时进时出->元素未完全进栈时，即可出栈。

栈的几种基本运算如下：

1.InitStack（&s）：初始化栈。构造一个空栈s。
2.DestroyStack（&s）：销毁栈。释放s占用的存储空间。
3.StackEmpty(s):判断栈是否为空；若空，则返回真，否则返回假。
4.Push(&s,e):进栈。将元素e插入到栈s中作为栈顶元素。
5.Pop（&s,e）：出栈。从栈s中退出栈顶元素，并将其值赋值给e。
6.GetTop(s,&e):取栈顶元素。返回当前的栈顶元素，并将其值赋值给e。

1.1.2顺序栈的结构、操作函数

顺序栈模型示意图：

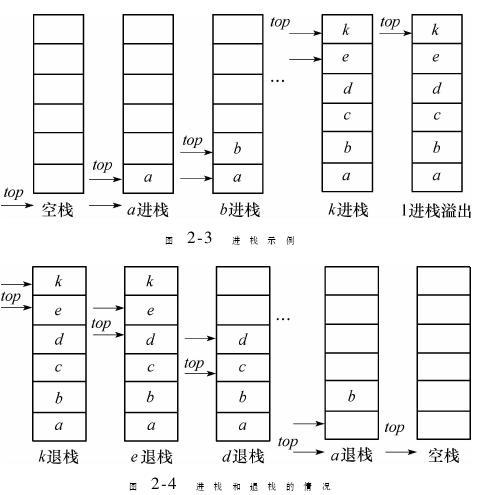
假设栈的元素个数最大不超过正整数MaxSize，所有的元素都具有同一数据类型ElemType，则栈类型SqStack：

typedef struct
{
 ElemType data[MaxSize];
 int top;  //栈顶指针
}Stack；
typedef Stack *SqStack;

顺序栈4要素：

·栈空条件：top=-1
·栈满条件：top=MaxSize-1
·进栈e操作：top++；st->data[top]=e
·退栈操作：e=st->data[top];top--;

基本运算

1)初始化栈InitStack（&s）

void InitStack（SqStack &s）
{
   s=new Stack;
   s->top=-1;
}

2)销毁栈ClearStack(&s)

void DestroyStack(SqStack &s)
{
 delete s;
}

3)判断栈是否为空StackEmpty(s)

bool StackEmpty(SqStack s)
{
 return (s->top==-1);
}

4)进栈Push（&s，e）

bool Push（SqStack &S,ElemType e)
{ 
   if(s->top==MaxSize-1)
       return false;
   s->top++;//栈顶指针+1
   s->data[s->top]=e;
   return true;
}

5）出栈Pop（&s，&e）

bool Pop（SqStack &s，ElemType &e）
{
 if(s->top==-1) //栈为空的情况，栈下溢出
    return false;
 e=s->data[s->top];//取栈顶指针元素
 s->top--; //栈顶指针-1
 return true;

}

6）取栈顶元素GetTop（s）

bool GetTop（SqStack *s，ElemType &e）
{
 if（s->top==1)//栈为空的情况
 return false;
 e=s->data[s->top];
 return true;
}

1.1.3链栈的结构、操作函数

链栈模型示意图

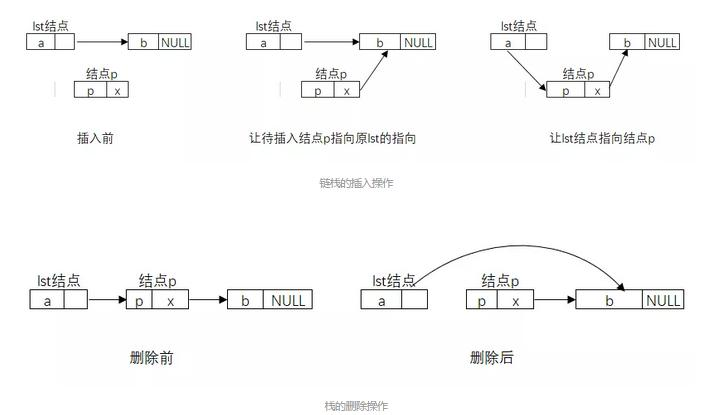
链栈中数据节点类型LiStack定义如下：

typedef int ElemType；
typedef struct linknode
{
  ElemType data；//数据域
  struct linknode *next；//指针域
}LiNode，*LiStack；

链栈4要素：

·栈空条件：s->next=NULL
·栈满条件：不考虑
·进栈e操作：结点插入到头结点后，链表头插法
·退栈操作：取出头结点之后的结点元素并删除之

基本运算

1)初始化栈InitStack（&s）

void InitStack（LiStack &s）
{
   s=new LiNode;
   s->next=NULL;
}

2)销毁栈ClearStack(&s)

void DestroyStack(LiStack &s)
{
  LiStack node;
  while(s!=NULL)
   {
     node=s;
     s=s->next;
     delete node;
   }
}

3)判断栈是否为空StackEmpty(s)

bool StackEmpty(LiStack s)
{
 return (s->next==NULL);
}

4)进栈Push（&s，e）

void Push（LiStack &S,ElemType e)
{ 
  LiStack p;
  p=new LiNode;
  p->data=e;
  p->next=s->next;
  s->next=p;
}

5）出栈Pop（&s，&e）

bool Pop（LiStack &s，ElemType &e）
{ 
 LiStack p;
 if(s->next==NULL) //栈空的情况
    return false;
 p=s->next;//p指向开始节点
 e=p->data;
 s->next=p->next;//删除*p节点
 delete p；//释放*p节点
 return true;

}

6）取栈顶元素GetTop（s）

bool GetTop（LiStack *s，ElemType &e）
{
 if（s->next==NULL)//栈为空的情况
   return false;
 e=s->next->data;
 return true;
}

1.2 栈的应用

表达式求值

中缀表达式：运算符号位于两个运算数之间。如：a+bc-d/e
后缀表达式：运算符号位于两个运算数之后。如：abc+de/-

中缀如何转后缀表达式：

1.优先级比栈顶运算符高入栈
2.低或相等，一直出栈到栈顶为空或者更高，写入后缀表达式
eg.表达式：(56-20)/(4+2)转为后缀表达式56#20#-4#2#+/
解析：“（”进栈，“-”进栈，“）”进栈，配对成功，“-”出栈；“/”进栈，“（”进栈，“+”进栈，“）”进栈，配对成功，“+”出栈；“/”还在栈底，“/”出栈。

1.3 队列

1.3.1画一个队列的图形：

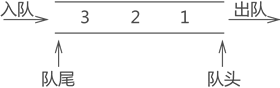
队列：只允许在表的一端进行插入，而在表的另一端进行删除的线性表。
队尾（rear）：允许插入的一端
队头（front）：允许删除的一端

队列特点：先进先出

基本运算

1.InitQueue(&q):初始化队列。构造一个空队列q。
2.DesttroyQueue(&q):销毁队列。释放队列q占用的储存空间。
3.QueueEmpty(q):判断队列是否为空。若队列q为空，则返回真；否则返回假。
4.enQueue(&q,e):进队列。将元素e进队作为队尾元素。
5.deQueue(&q,&e):出队列。从队列q中出队一个元素，并将其值赋值给e。

1.3.2顺序队列的结构、操作函数

需要定义两个指针（top 和 rear）分别用于指向顺序队列中的队头元素和队尾元素：

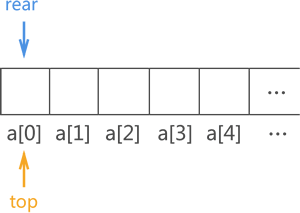
结构定义：

typedef struct
{
 ElemType data[MaxSize];
 int front,rear; //队首和队尾指针
}Queue；
typedef Queue *SeQueue；

顺序队的四要素

·队空条件：front=rear
·队满条件：rear=MaxSize-1
·元素e进队：rear++；data[rear]=e;
·元素e出队：front++；e=data[front];

基本运算

1）初始化队列：InitQueue(&q)

void InitQueue（SqQueue &q）
{
 q=new Queue；
 q->front=q->rear=-1;
}

2)销毁队列DestroyQueue(q)

void DestroyQueue(SqQueue &q)
{
 delete q;
}

3)判断队列是否为空QueueEmpty（q)

bool QueueEmpty(SqQueue q)
{
 return(q->front==q->rear);
}

4)进队列enQueue（q，e）

bool enQueue(SqQueue &q,ElemType e)
{
 if(q->rear+1==MaxSize)
   return false;   //队满上溢出
  q->rear=q->rear+1;
  q->data[q->rear]=e;
  rerurn true;
}

5)出队列deQueue(q,e）

bool deQueue(SqQueue &q,ElemType &e)
{
 if(q->front==q->rear)//队空下溢出
   return false；
 q->front=q->front-1;
 e=q->data[q->front];
 return true;
}

1.3.3环形队列的结构、操作函数

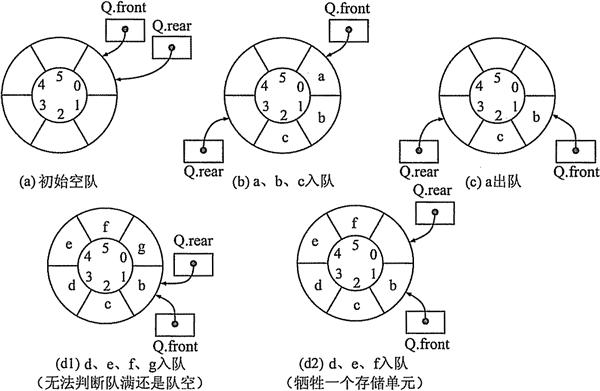
环形队列结构体：

typedef struct
{
  ElemType data[MaxSize];
  int front,rear;
}Queue;
typedef Queue *SqQueue；

环形队列采用rear==MaxSize-1作为队满条件，当队满条件为真时，队中可能还有若干个空位置，这种溢出称为假溢出。

基本运算

1）初始化队列

void InitQueue(SqQueue &q)
{
  q=new Queue;
  q->front=q->rear=0;
}

2）进环形队列

bool enQueue(SqQueue &q,Elemtype e)
{
  if((q->rear+1)%MaxSize==q->front)//队满上溢出
      return false;
  q->rear=(q->rear+1)%MaxSize;//移动rear
  q->data[q->rear]=e;
  return true;
}

3）出环形队列

bool deQueue(SqQueue &q,Elemtype e)
{
  if(q->front==q->rear)//队空下溢出
  return false
  e=q->data[q->front];
  q->front=(q->front+1)%MaxSize;//移动front
  return true;
}

*销毁队列&判断队列是否为空同顺序队列操作相同。

1.3.4链队列的结构、操作函数

链式队列的实现思想同顺序队列类似，只需创建两个指针分别指向链表中队列的队头元素和队尾元素：

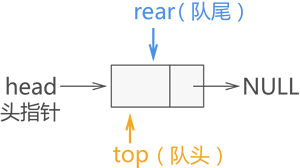
链队中头尾指针类型LinkQueue定义：

typedef struct
{
  QNode *front;
  QNode *rear;
}LinkQueue;

链队的4要素

·队空条件：front=rear=NULL
·队满条件：不考虑
·进队e操作：将包含e的节点插入到单链表表尾
·出队操作：删除单链表首数据节点

基本运算

1）初始化链队列

void InitQueue(LinkQuNode &q)
{
   q=new LinkQuNode;
   q->front=q->rear=NULL;
}

2)进队列

bool enQueue(LinkQuNode &q,ElemType e)
{
   p=new QNode;
   p->data=e;//新建结点
   p->next=NULL;//避免后面无结束
   q->rear->next=p;
   q->rear=p;//尾指针移动
}

3)出队列

bool deQueue(LinkQuNode &q,ElemType e)
{
    Node t;
    if(q->rear==NULL)
    return false;
    t=q->front;
    if(q->front==q->rear）//此时只有一个数据
    {
       q->front=q->rear=NULL;
    }
    else
    {
       q->front=q->front->next;//移动front
    }
    e=t->data;
    delete t;//删除
}

1.3.5队列应用。

操作系统

售票系统

打印机

手机短信发送

2.PTA实验作业

7-2 jmu-ds-符号配对
 7-6 银行业务队列简单模拟

2.1 符号配对

2.1.1 解题思路及伪代码

解题思路：将字符一个一个处理，发现一个要处理的左符号“[,(,{”就入栈，发现一个需要处理的右符号“],),}”就与栈顶对比，如果是对应的左符号，那么把栈顶弹出，否则说明这个右符号不能配对，输出NO等信息并退出。如果一直处理到程序结尾都没有退出就是YES。

2.1.2 总结解题所用的知识点

本题需要考虑到左符号剩余，右符号剩余，配对情况，不配对情况，需要多重if 来进行约束判断。
伪代码：

 定义字符型数组s 
 输入s
    for（循环i=0 to i<len）
 {   
    if（不是符号 ）
        跳过以下语句
    if（为左符号 ）进栈
    else if（为右符号）
        {
             if（ 栈空） 退出程序
             else if（为右符号且配对） 出栈
        }           
 } 结束for循环
//判断是否配对成功
    if（栈空且i=len）  配对成功，输出“yes”
    else if（i不等于len） 配对失败，输出“no”以及栈顶（栈为空不输出）

2.2 银行业务队列简单模拟

2.2.1 解题思路及伪代码

解题思路：这道题的意思就是模拟队列，将偶数的数字存到b窗口，将奇数的数字存到a窗口，而且是先进先出，所以可以采用队列，将偶数的放在b队列，将奇数的放在a队列；然后每输出两个a队列中的元素，再输出一个b队列中的元素；
伪代码：

queue<int> oddQu， evenQu;//定义两个队列
	int N，i=0，num,evenLength,oddLength;
        cin >> N;
 while(i<N)
{
   输入num；
   if（num为偶数）  放在队列evenQu；
      else  （num为奇数） 放在队列oddQu；
}
。。。

2.2.2 总结解题所用的知识点

queue相关函数的使用、本题需要考虑a队列其个数以及奇偶性。

3.阅读代码（

3.1 题目及解题代码

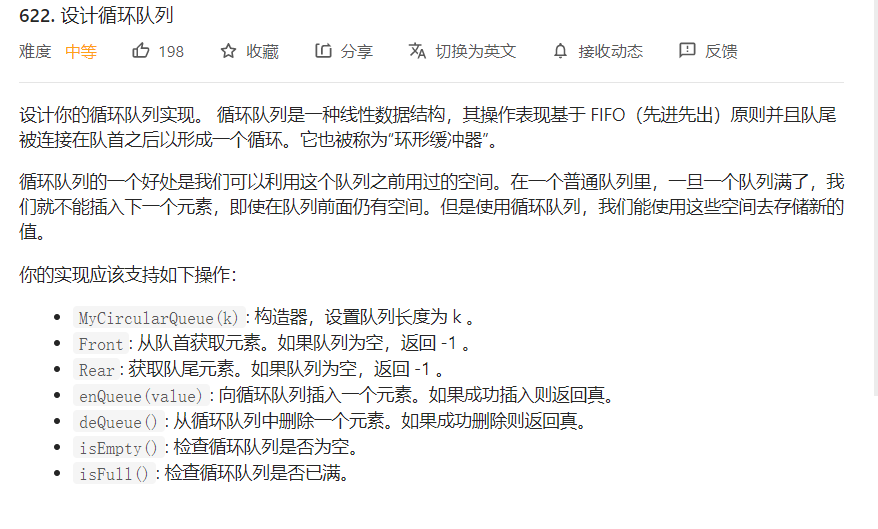
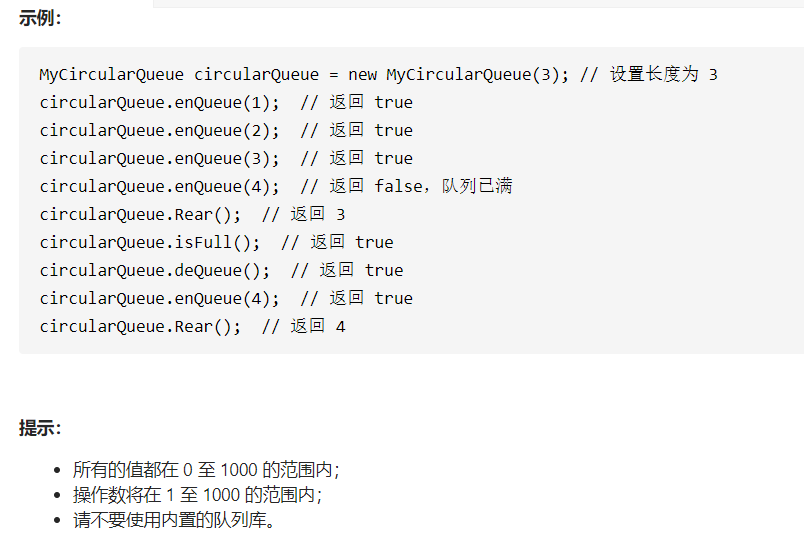
class MyCircularQueue {
private:
	int *data;
	int front, rear;
	int len;
public:
	MyCircularQueue(int k) {
		data = new int[k];
		front = rear = -1;
		len = k;
	}

	~MyCircularQueue() {
		delete[] data;
	}

	bool enQueue(int value) {
		if (isFull())
			return false;
		if (isEmpty())
			front++;
		rear = (rear + 1) % len;//rear后移一位,若到最后则转到数组头部
		data[rear] = value;
		return true;
	}

	bool deQueue() {
		if (isEmpty())
			return false;
		if (front == rear && front != -1)//只剩一位
			front = rear = -1;
		else
			front = (front + 1) % len;
		return true;
	}

	int Front() {
		if (isEmpty())
			return -1;
		return data[front];
	}

	int Rear() {
		if (isEmpty())
			return -1;
		return data[rear];
	}

	bool isEmpty() {
		return (front == rear && front == -1);
	}

	bool isFull() {
		return ((rear + 1) % len == front);
	}
};

作者：Roycec
链接：https://leetcode-cn.com/problems/design-circular-queue/solution/cdong-tai-shu-zu-shi-xian-by-roycec-g3qn/
来源：力扣（LeetCode）

3.2 该题的设计思路及伪代码

posted @ 2021-04-05 22:15 SUEHUNG 阅读(119) 评论(0) 收藏举报

刷新页面返回顶部

DS博客作业02--栈和队列

0.PTA得分截图

1.本周学习总结

1.1 栈

1.1.1画一个栈的图形：

栈中元素的特性：

栈的进栈出栈规则：

栈的几种基本运算如下：

1.1.2顺序栈的结构、操作函数

顺序栈模型示意图：

顺序栈4要素：

基本运算

1.1.3链栈的结构、操作函数

链栈模型示意图

链栈4要素：

基本运算

1.2 栈的应用

表达式求值

中缀如何转后缀表达式：

1.3 队列

1.3.1画一个队列的图形：

队列特点：先进先出

基本运算

1.3.2顺序队列的结构、操作函数

结构定义：

顺序队的四要素

基本运算

1.3.3环形队列的结构、操作函数

环形队列 结构体：

基本运算

1.3.4链队列的结构、操作函数

链队中头尾指针类型LinkQueue定义：

链队的4要素

基本运算

1.3.5队列应用。

操作系统

售票系统

打印机

手机短信发送

2.PTA实验作业

2.1 符号配对

2.1.1 解题思路及伪代码

2.1.2 总结解题所用的知识点

2.2 银行业务队列简单模拟

2.2.1 解题思路及伪代码

2.2.2 总结解题所用的知识点

3.阅读代码（

3.1 题目及解题代码

3.2 该题的设计思路及伪代码

公告

环形队列结构体：