2.19

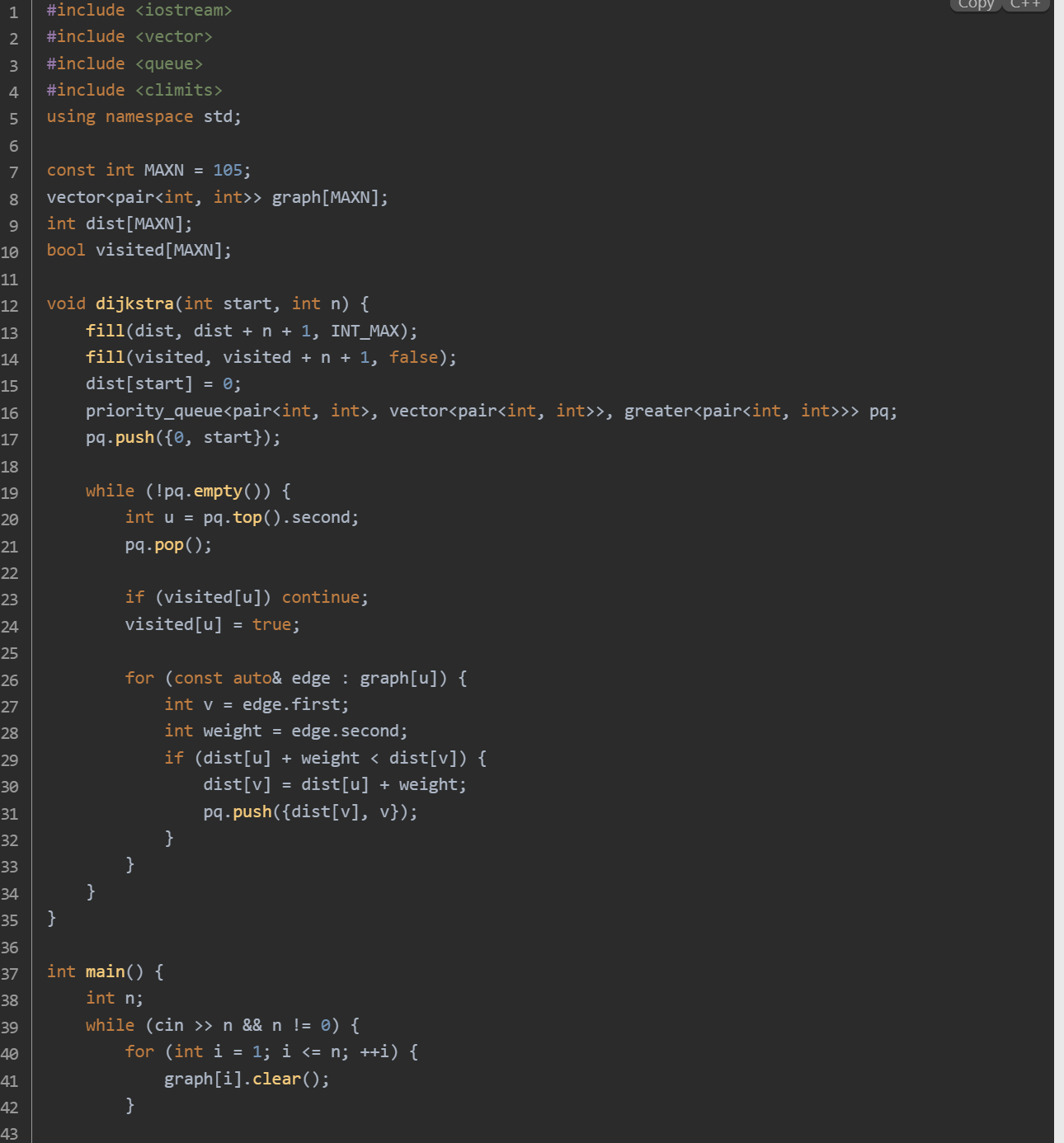
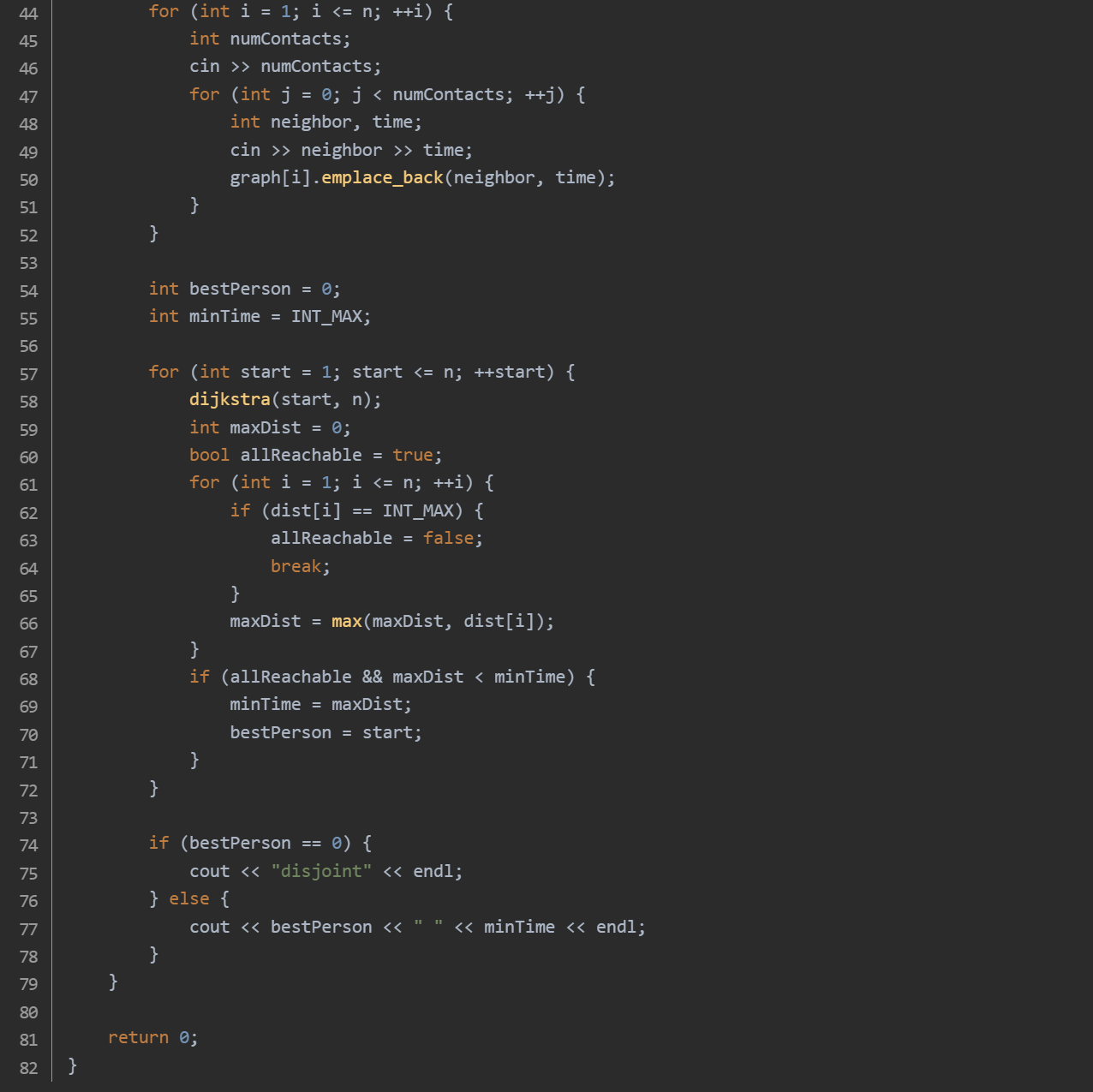
思路：读取输入的节点数 n，并循环处理每个数据集，直到 n 为 0。对于每个数据集，读取每个节点的邻接信息并构建图。遍历每个节点作为起点，调用 dijkstra 算法计算最短路径。检查是否所有节点都可达，如果可达则记录最大距离，并更新最佳节点和最小时间。最后输出结果，如果没有找到合适的节点则输出 disjoint。

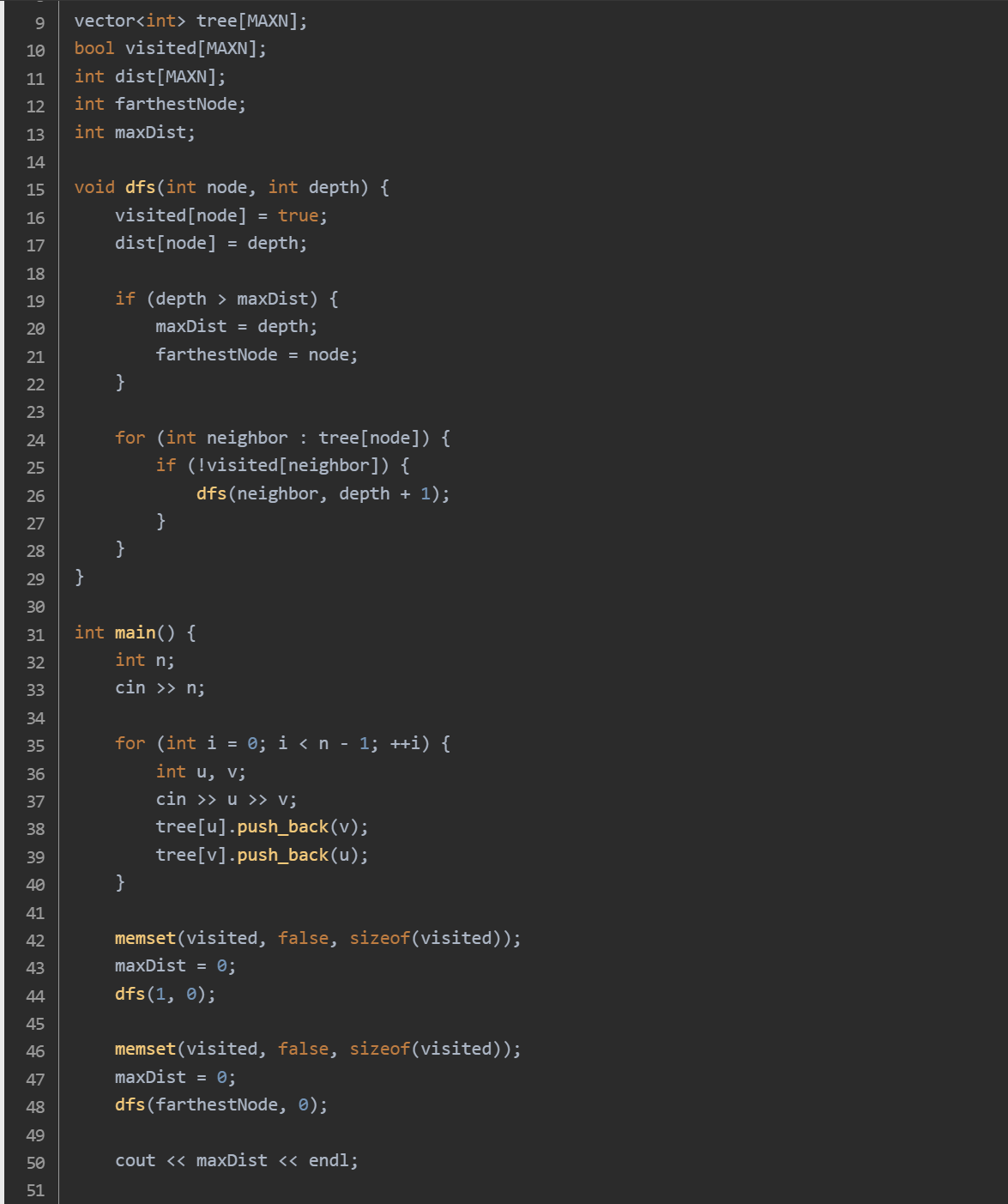
思路：从任意一个节点开始进行第一次 DFS，找到距离该节点最远的节点 x。从节点 x 开始进行第二次 DFS，找到距离节点 x 最远的节点 y。节点 x 到节点 y 的路径就是树的直径。记录第二次 DFS 过程中到达最远节点的距离，该距离即为树的直径包含的边的个数。

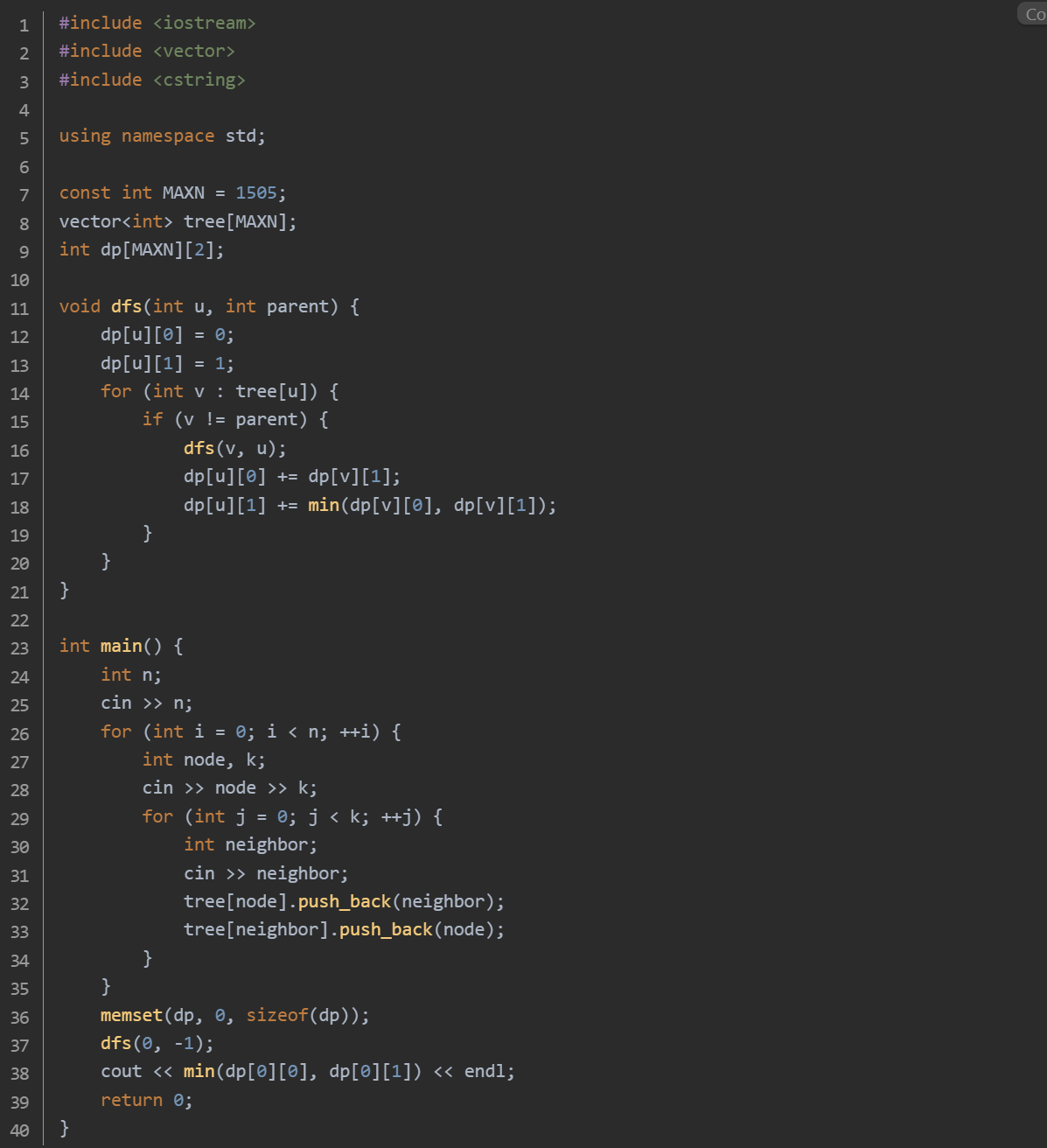
思路：首先读取节点的数量 n。接着循环 n 次，对于每个节点，读取其编号 node 和与之相连的边的数量 k，再读取这 k 条边的另一个端点 neighbor，将边信息存储在邻接表 tree 中，由于是无向边，所以需要双向添加。dp[i][0] 表示节点 i 不放置士兵时，以节点 i 为根的子树所需的最少士兵数量。dp[i][1] 表示节点 i 放置士兵时，以节点 i 为根的子树所需的最少士兵数量。对于当前节点 u，初始化 dp[u][0] = 0，dp[u][1] = 1，因为不放置士兵时初始为 0，放置士兵时初始为 1。遍历 u 的所有邻接节点 v，如果 v 不是 u 的父节点（避免重复遍历），则递归调用 dfs(v, u) 计算以 v 为根的子树的状态。对于 dp[u][0]，由于 u 不放置士兵，那么其所有子节点都必须放置士兵，所以 dp[u][0] += dp[v][1]。对于 dp[u][1]，由于 u 放置士兵，那么其子节点可以放置也可以不放置，取两者中的最小值，即 dp[u][1] += min(dp[v][0], dp[v][1])。从根节点（这里选择节点 0 作为根节点）开始进行深度优先搜索，最终结果为 min(dp[0][0], dp[0][1])。


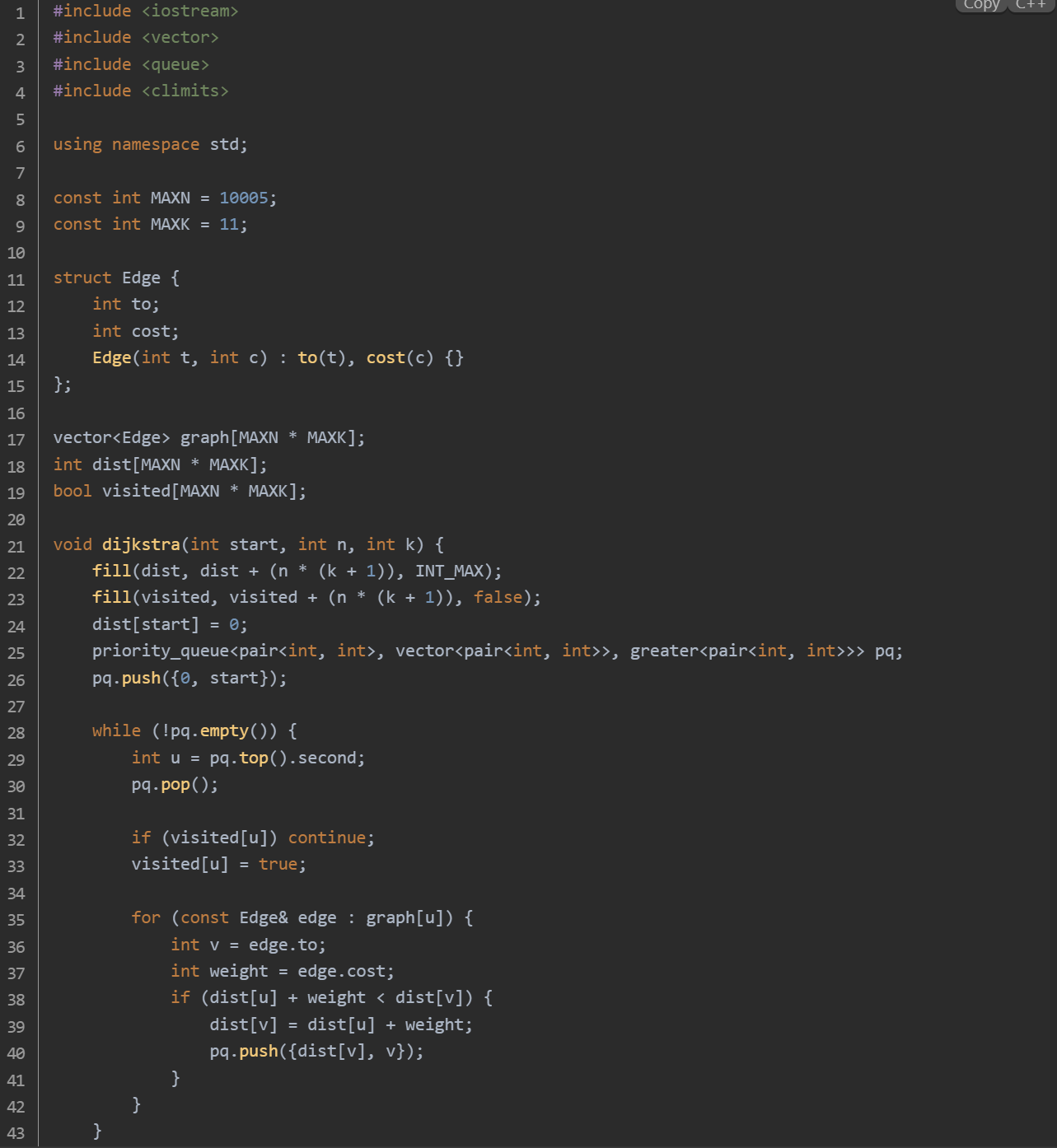
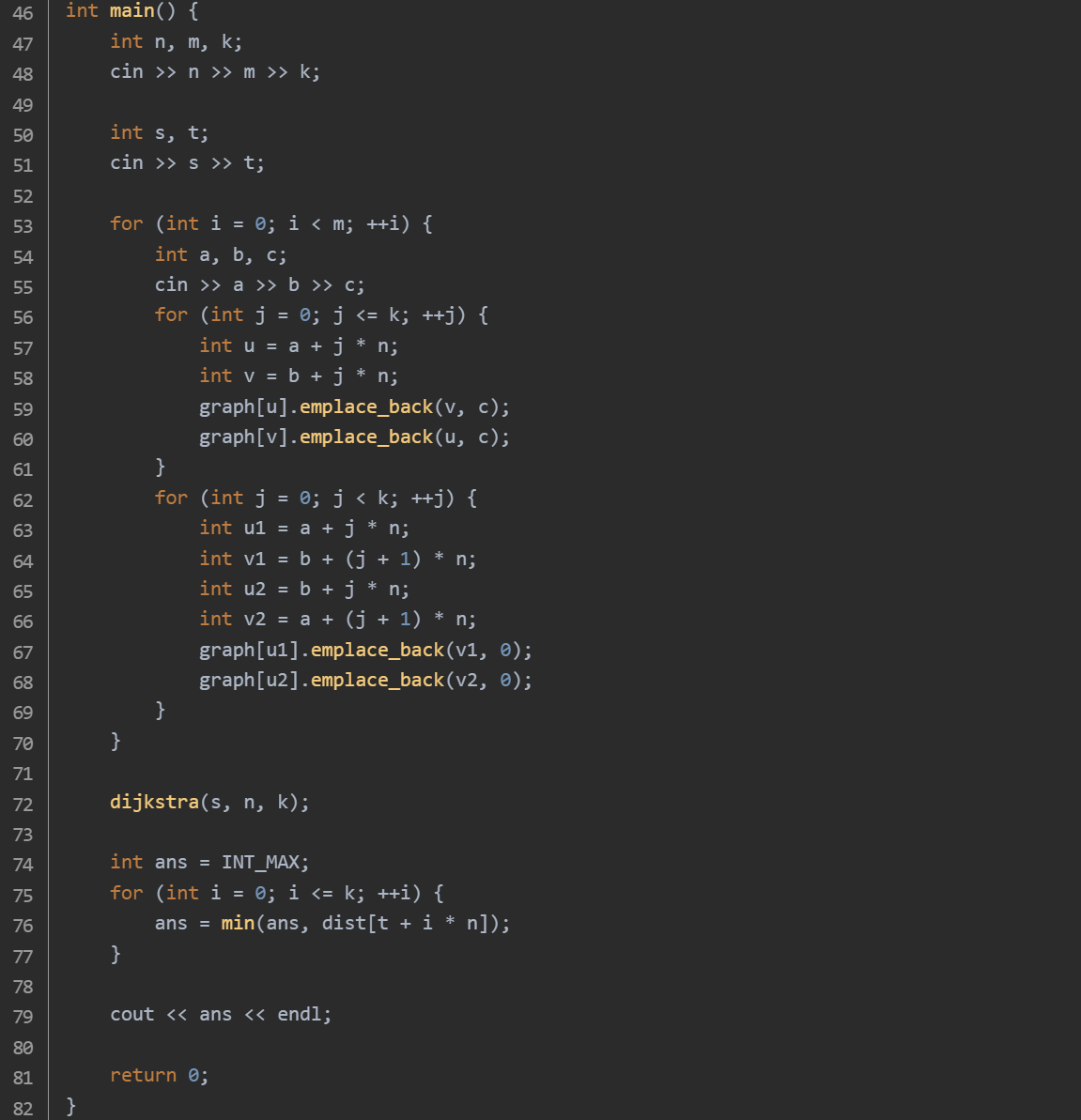
思路：结构体 Edge：用于表示图中的边，包含目标节点 to 和边的费用 cost。邻接表存储分层图：使用 graph 存储分层图，graph[i] 存储与节点 i 相邻的所有节点及其边权。Dijkstra 算法：dijkstra 函数实现了 Dijkstra 算法，用于计算从起点到各个节点的最短路径。使用优先队列优化，提高算法效率。主函数逻辑：读取城市数 n、航线数 m 和免费乘坐次数 k。读取起点 s 和终点 t。读取每条航线的信息，在同一层图内添加边，在相邻两层图之间添加免费边。调用 dijkstra 算法计算从起点到各个节点的最短路径。找到终点在各层图中的最小距离，即为最少花费。

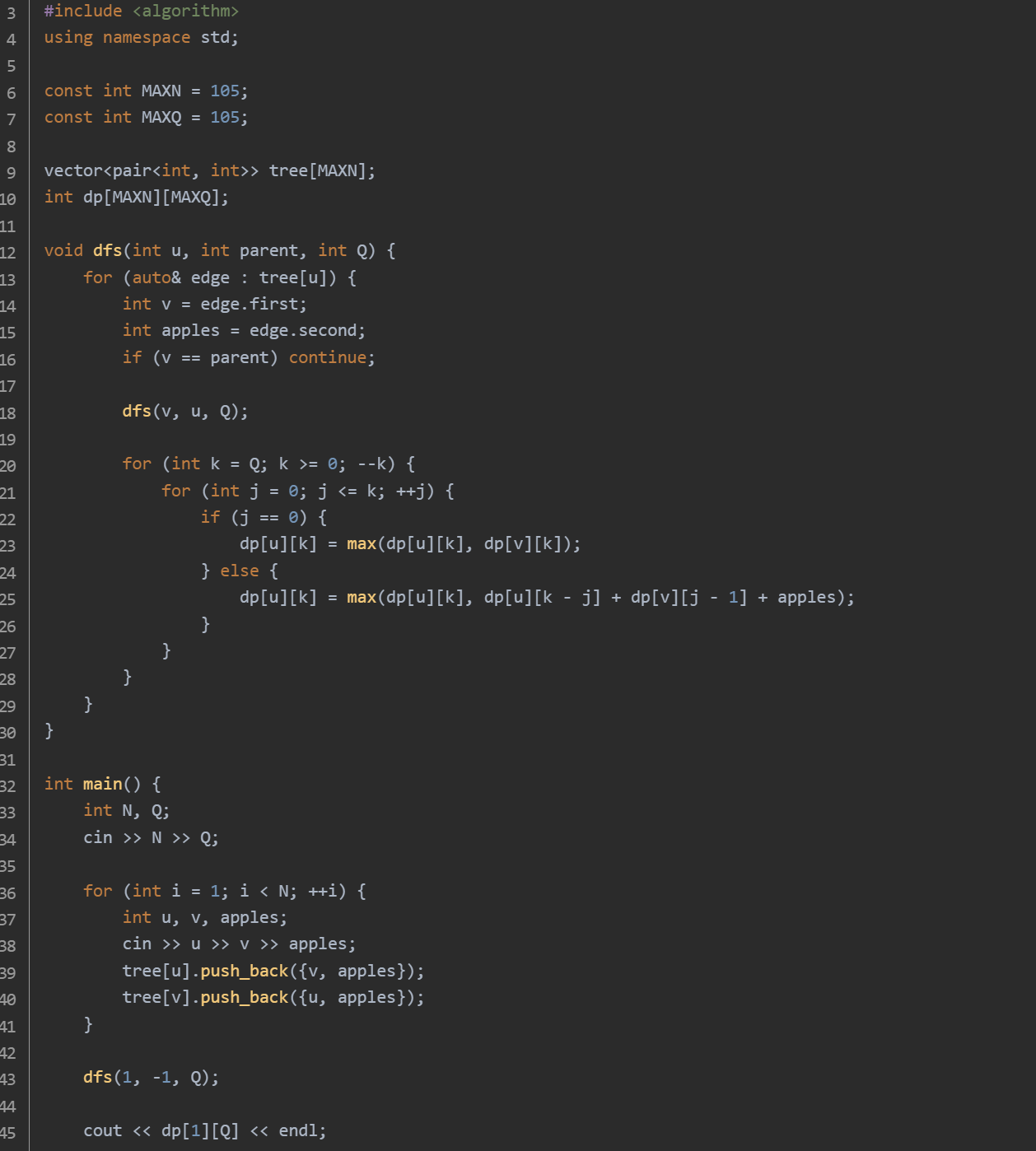
思路：树的表示：使用邻接表 tree 来存储树的结构，每个节点存储其子节点和对应的苹果数量。DFS 遍历：从根节点开始进行 DFS 遍历，递归处理每个子节点。动态规划更新：对于每个节点 u，我们遍历其子节点 v，并根据是否保留连接 u 和 v 的树枝来更新 dp[u][k]。输出结果：最终输出 dp[1][Q]，即以根节点为根的子树中保留 Q 条树枝的最大苹果数量。

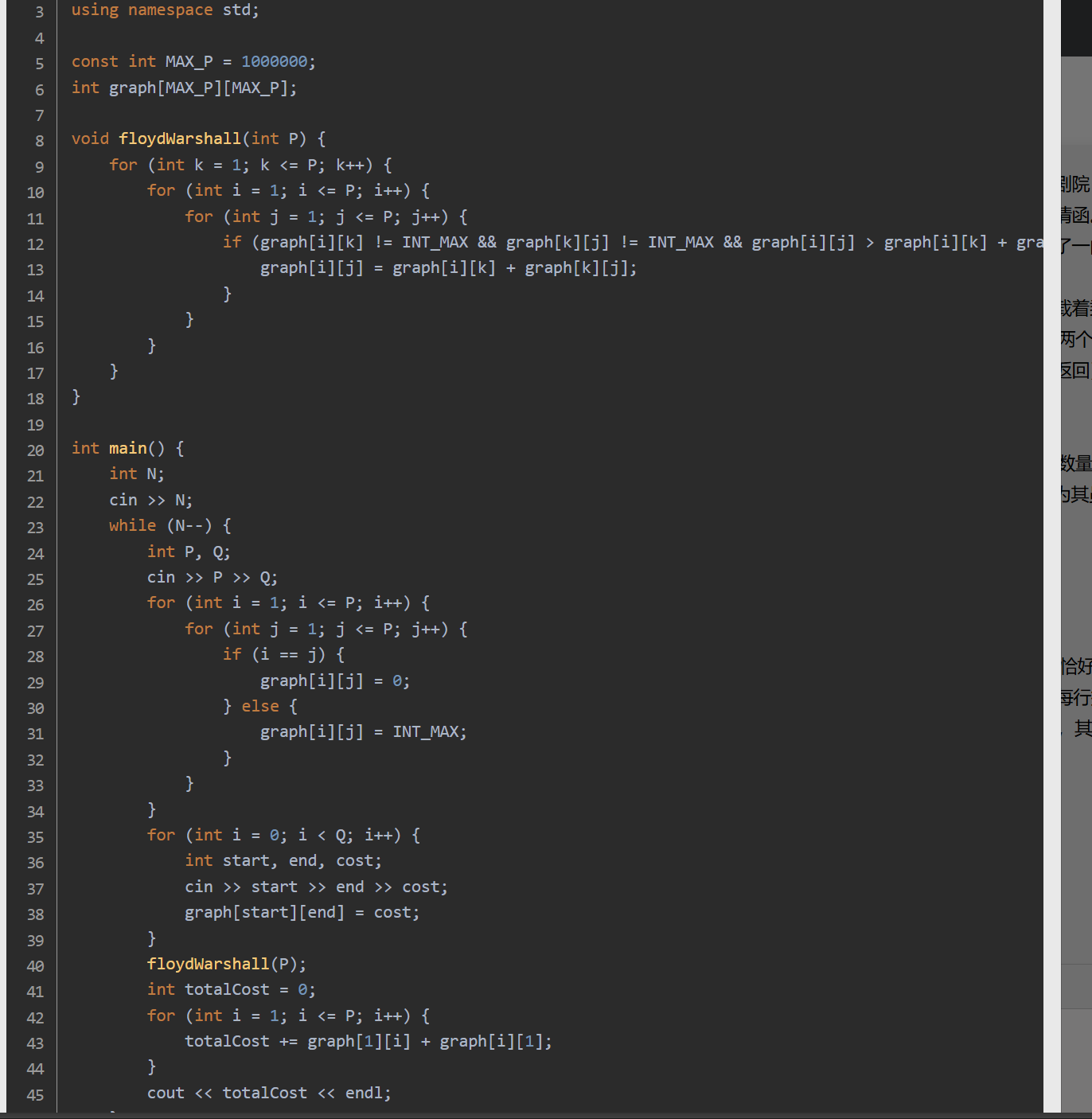
思路：定义 graph 二维数组存储公交路线价格信息。floydWarshall 函数实现弗洛伊德算法，计算任意两点之间的最短路径。在 main 函数中：读入案例数量、站点数量和公交路线数量。初始化 graph 数组。读入公交路线信息并更新 graph。调用 floydWarshall 计算最短路径。计算并输出总费用。
学习总结：
图的基本概念与表示
邻接表：是图的一种常用存储方式，适用于稀疏图。在多道题目中均有使用，如树的存储（树是一种特殊的图）。在求树的直径、树中放置士兵问题以及苹果树剪枝问题里，使用邻接表存储图（树）的结构，每个节点的邻接信息以列表形式存储，便于进行深度优先搜索（DFS）等操作。例如在树的直径问题中，vector tree[MAXN] 存储了树的节点连接关系；在苹果树剪枝问题中，vector tree[MAXN] 不仅存储了节点连接关系，还存储了边的权重（苹果数量）。
邻接矩阵：适用于稠密图，在公交路线费用问题中使用邻接矩阵 graph[MAX_P][MAX_P] 存储公交路线的价格信息，矩阵元素 graph[i][j] 表示从站点 i 到站点 j 的费用。
图的遍历算法
深度优先搜索（DFS）：是一种重要的图遍历算法，通过递归或栈的方式实现。在树的直径问题中，通过两次 DFS 找到树的直径，第一次 DFS 从任意节点出发找到距离该节点最远的节点 x，第二次从节点 x 出发找到距离 x 最远的节点 y，节点 x 到节点 y 的路径即为树的直径；在树中放置士兵问题和苹果树剪枝问题中，DFS 用于遍历树的节点，根据节点状态进行动态规划的状态转移。
广度优先搜索（BFS）：在提供的思路中未明确体现，但也是一种常用的图遍历算法，常用于求解最短路径问题（无权图），使用队列实现。
最短路径算法
Dijkstra 算法：用于求解单源最短路径问题，适用于边权非负的图。在公交志愿者交通费用问题和乘飞机旅行最少花费问题中使用。通过优先队列优化，时间复杂度可达到 ，其中 是节点数， 是边数。在乘飞机旅行最少花费问题中，还使用了分层图的思想，构建 k + 1 层图，每一层表示使用不同次数免费搭乘机会的状态，在分层图上使用 Dijkstra 算法求解最短路径。
Floyd - Warshall 算法：用于求解任意两点之间的最短路径问题，时间复杂度为 ，其中 是节点数。在公交路线费用问题中，使用该算法计算任意两个站点之间的最短路径，适用于节点数较少的情况。
动态规划在图论中的应用
树形动态规划：在树的相关问题中应用广泛，如树中放置士兵问题和苹果树剪枝问题。通过定义状态和状态转移方程，利用 DFS 遍历树的节点进行状态转移。在树中放置士兵问题中，定义 dp[i][0] 和 dp[i][1] 分别表示节点 i 不放置和放置士兵时以节点 i 为根的子树所需的最少士兵数量；在苹果树剪枝问题中，dp[u][k] 表示以节点 u 为根的子树保留 k 条树枝的最大苹果数量。
分层图动态规划：在乘飞机旅行最少花费问题中，通过构建分层图，将使用不同次数免费搭乘机会的状态分层表示，然后使用 Dijkstra 算法进行状态转移，最终找到最少花费。
特殊图结构问题
树的直径：通过两次 DFS 可以在线性时间内求解树的直径，这是树结构的一个重要性质，在很多实际问题中有应用。
无根树的处理：在树的相关问题中，很多树是无根树，但可以任选一个节点作为根节点进行处理，不影响问题的求解，如树的直径、树中放置士兵问题等。