2.17

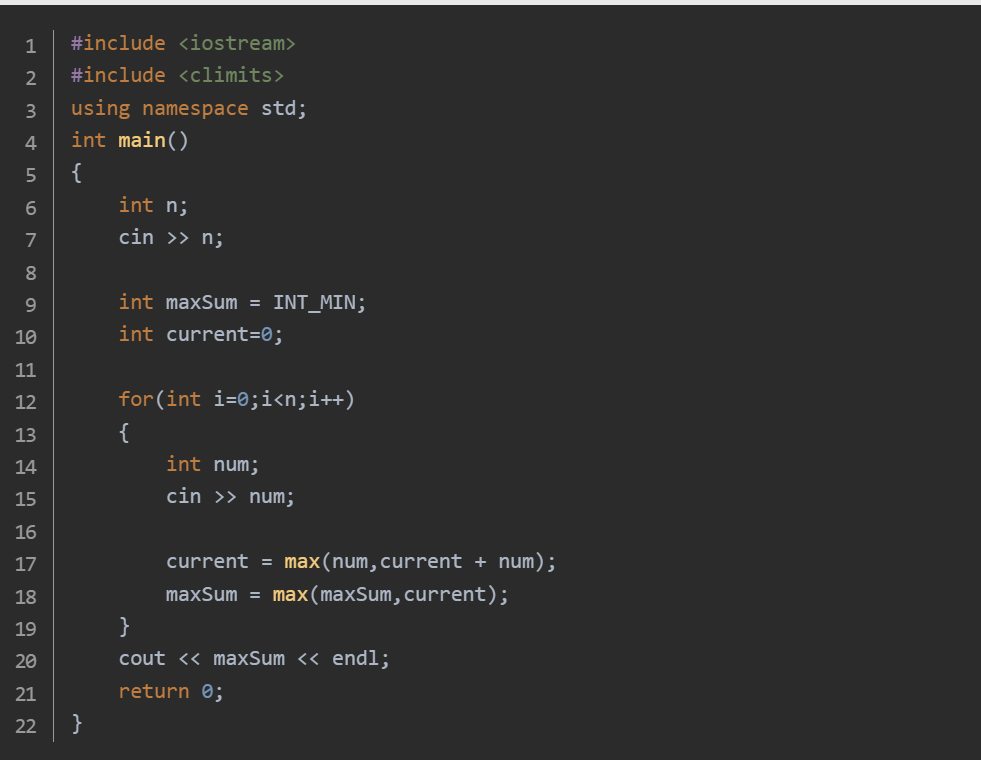
思路：max_sum 设为极小值，用来存最大子段和。current_sum 设为 0，存当前子段和。对每个元素 num，更新 current_sum 为 max(num, current_sum + num)。这意味着要么以 num 开始新子段，要么把 num 加入当前子段，取和更大的情况。再用 max(max_sum, current_sum) 更新 max_sum。遍历完后，max_sum 就是所求的最大子段和

思路：创建一个长度为 T + 1 的数组 dp，其中 dp[i] 表示在时间为 i 的情况下能采到的草药的最大总价值，初始值都为 0。外层循环遍历每一株草药。内层循环从最大时间 T 开始递减到当前草药的采摘时间，对于每个时间 j，比较不采当前草药（dp[j]）和采当前草药（dp[j - times[i]] + values[i]）哪种情况能得到更大的价值，取最大值更新 dp[j]。最终 dp[T] 即为在规定时间 T 内可以采到的草药的最大总价值。

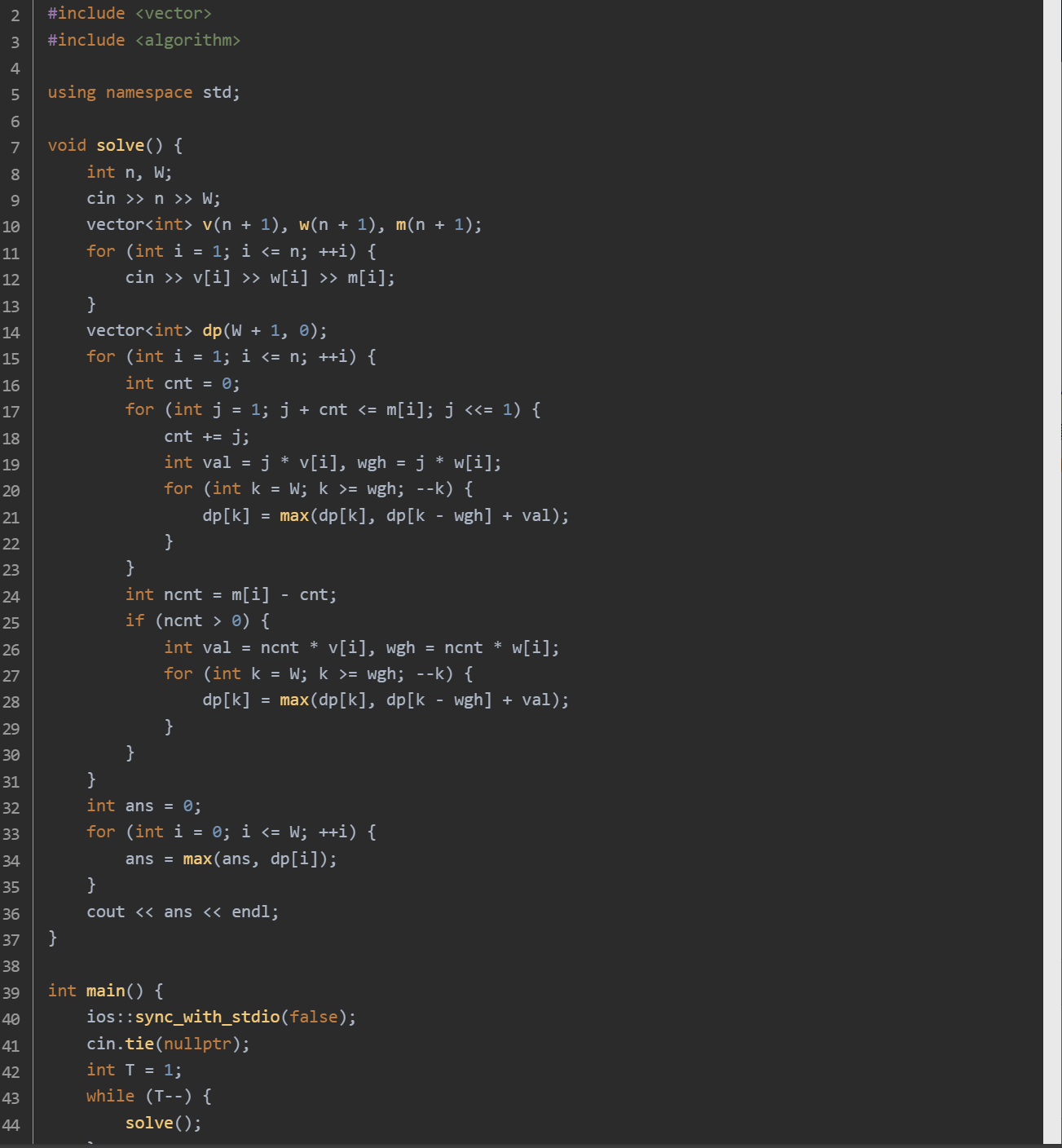
思路：首先读取宝物种数 n 和采集车的最大载重 W，接着读取每种宝物的价值 v[i]、重量 w[i] 和数量 m[i]。对于每种宝物，通过二进制拆分的方式将其数量 m[i] 拆分成若干个不同的 2 的幂次方之和。例如，若 m[i] = 13，可以拆分为 1 + 2 + 4 + 6。将拆分后的每个 “新物品” 看作一个 0 - 1 背包问题中的物品，进行状态转移。状态转移方程为 dp[k] = max(dp[k], dp[k - wgh] + val)，其中 dp[k] 表示载重为 k 时能获得的最大价值，wgh 是当前 “新物品” 的重量，val 是其价值。

思路：首先读取排列的长度 ，然后读取排列 并记录每个元素的位置，接着读取排列 并将其元素替换为在 中的位置，存储在 new_seq 中。使用 lis 数组来存储最长上升子序列，遍历 new_seq 中的每个元素，通过 lower_bound 函数二分查找第一个大于等于该元素的位置，如果该位置在数组末尾，则将该元素添加到数组末尾，否则替换该位置的元素。最后输出 lis 数组的长度，即为最长公共子序列的长度。

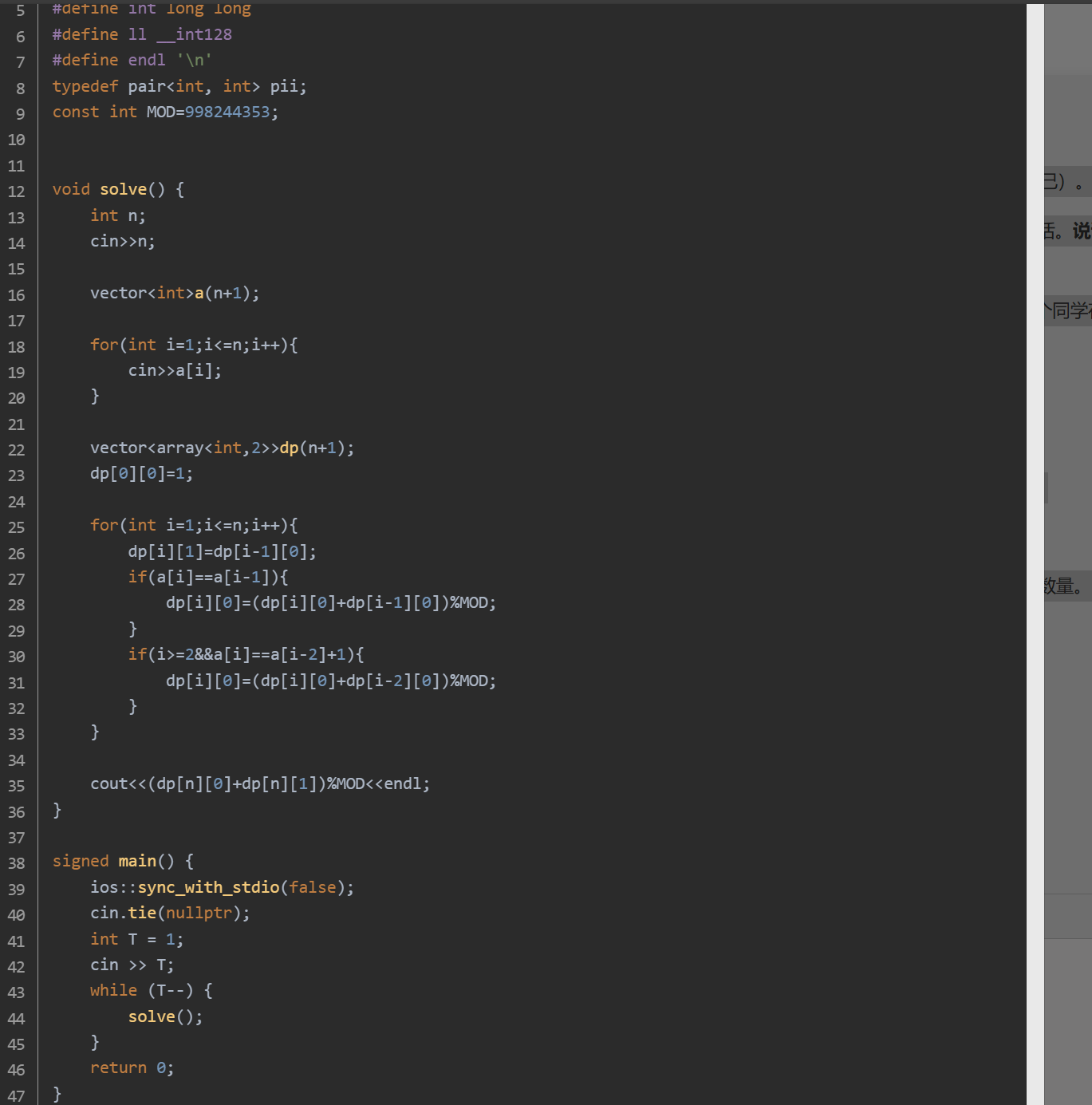
思路：dp[i][0] 表示考虑前 i 个人，且第 i 个人是诚实的情况下的合法配置数量；dp[i][1] 表示考虑前 i 个人，且第 i 个人是说谎的情况下的合法配置数量。当第 i 个人说谎时，由于不能有两个连续的说谎者，所以第 i - 1 个人必须是诚实的，即 dp[i][1] = dp[i - 1][0]。当第 i 个人诚实时，需要分情况讨论：如果第 i 个人声称的左边说谎者数量和第 i - 1 个人相同，说明第 i - 1 个人也可以是诚实的，那么 dp[i][0] 可以从 dp[i - 1][0] 转移过来。如果 i >= 2 且第 i 个人声称的左边说谎者数量等于第 i - 2 个人声称的数量加 1，说明第 i - 1 个人是说谎者，第 i - 2 个人是诚实的，那么 dp[i][0] 可以从 dp[i - 2][0] 转移过来。

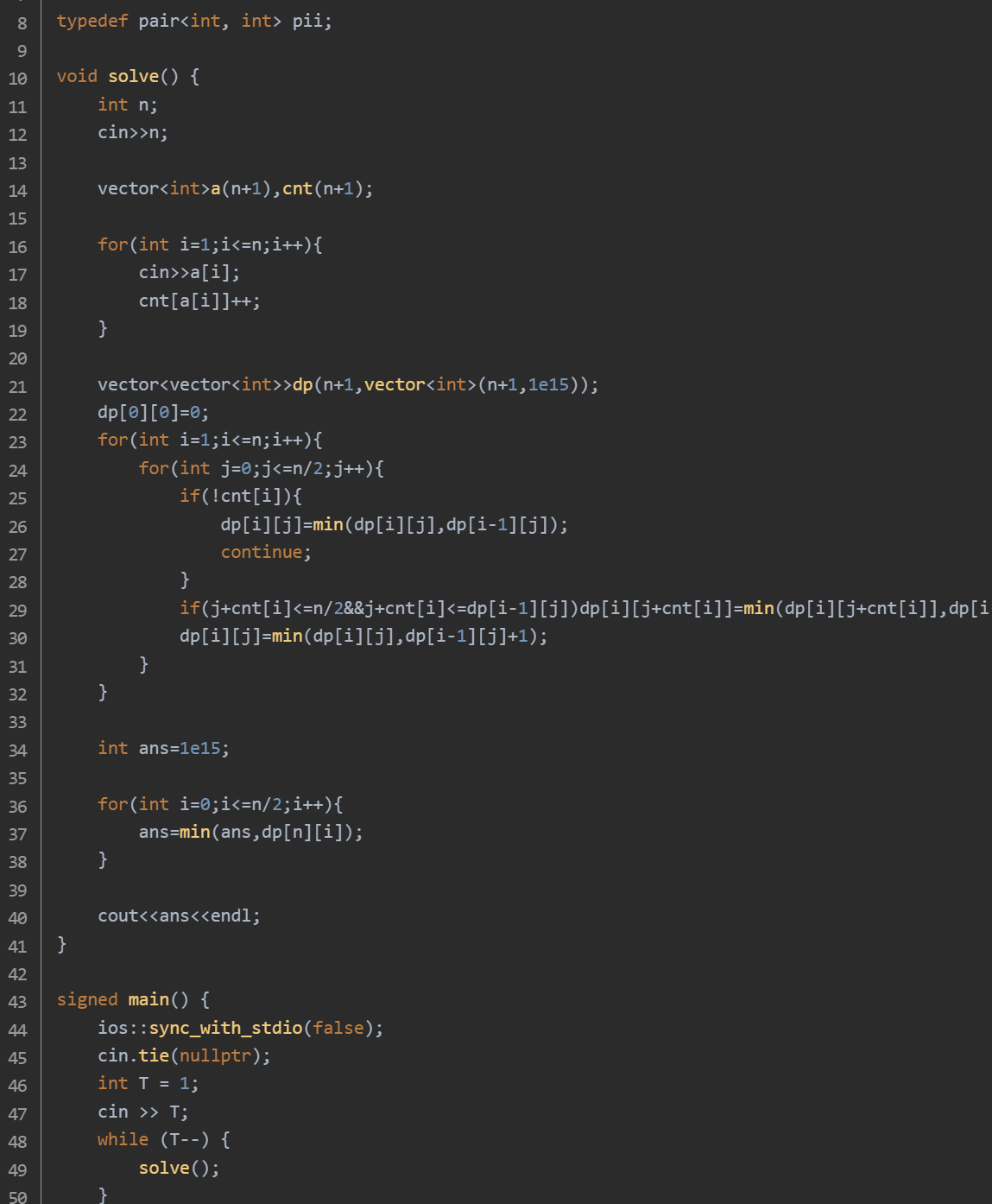
思路：读取蛋糕的总数 n。读取每个蛋糕的大小并统计每种大小蛋糕的数量。dp[i][j] 表示考虑到大小为 i 的蛋糕，Bob 拿了 j 次蛋糕时，Alice 获得蛋糕的最少数量。初始状态 dp[0][0] = 0，表示还没开始拿蛋糕时，Alice 获得 0 个蛋糕。通过两层循环遍历蛋糕大小和 Bob 拿蛋糕的次数进行状态转移：若当前大小蛋糕数量为 0，则直接继承上一个状态。否则，考虑两种情况：不拿当前大小蛋糕，Alice 获得蛋糕数加 1；拿当前大小蛋糕，需要满足一定条件才能更新状态。遍历 dp[n][i]（i 从 0 到 n / 2），找出 Alice 获得蛋糕的最小数量并输出。
学习总结：
1.线性动态规划
最大子段和问题
适用场景：处理连续子序列的最优值问题，例如在整数序列中找最大和的连续子段。
实现要点：只需维护两个变量 max_sum 和 current_sum，通过一次遍历序列不断更新这两个变量，时间复杂度为 ，空间复杂度为 。
2.背包问题
0 - 1 背包问题（采药问题）
适用场景：在有限资源（如时间、重量）限制下，从多个物品中选择部分物品，使总价值最大，每个物品只能选一次。
实现要点：使用一维数组 dp 记录不同资源状态下的最大价值，通过两层循环，外层遍历物品，内层从资源上限递减到当前物品所需资源进行状态转移，时间复杂度为 ，空间复杂度为 ，其中 是物品数量， 是资源上限。
3.多重背包问题（宝物采集问题）
适用场景：与 0 - 1 背包类似，但每种物品有一定数量限制。
实现要点：通过二进制拆分将多重背包转化为 0 - 1 背包问题，减少物品数量，降低时间复杂度。将每种物品的数量拆分为 2 的幂次方之和，把拆分后的 “新物品” 按 0 - 1 背包处理
4.最长公共子序列问题（排列 LCS 转化为 LIS）
对于排列问题，可将其转化为最长上升子序列（LIS）问题。先记录一个排列中元素的位置，将另一个排列元素替换为对应位置得到新序列，再用二分查找优化的方法求解新序列的 LIS，时间复杂度为 ，空间复杂度为 。
5.状态限制问题（同学诚实说谎问题）
通过定义多个状态（如 dp[i][0] 表示第 i 个人诚实，dp[i][1] 表示第 i 个人说谎），根据限制条件进行状态转移，在状态转移过程中考虑限制条件对状态的影响，时间复杂度为 ，空间复杂度为 。
6.博弈类动态规划（蛋糕分配问题）
定义状态表示不同阶段的博弈结果，如 dp[i][j] 表示考虑到某种情况（如蛋糕大小），一方（如 Bob）进行了 j 次操作时另一方（如 Alice）的最优结果。根据博弈规则进行状态转移，考虑不同操作选择对结果的影响。