2.10

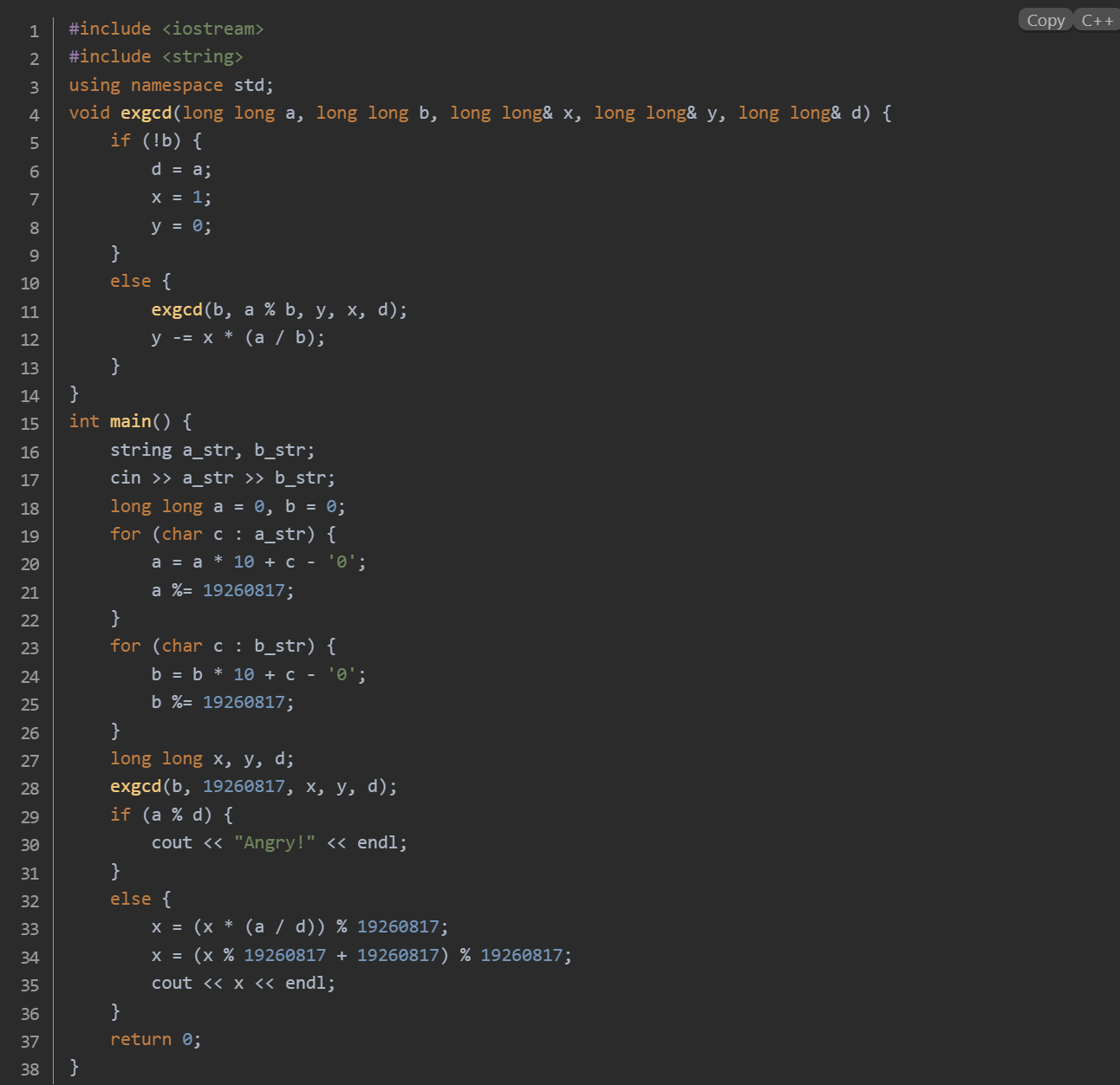
思路：从标准输入读取两个大整数，并将它们对19260817取模以避免溢出。使用扩展欧几里得算法求解的一组整数解以及最大公约数。根据同余方程有解的充要条件判断方程是否有解。若方程有解，求出最小非负整数解并输出；若无解，输出 "Angry!"。

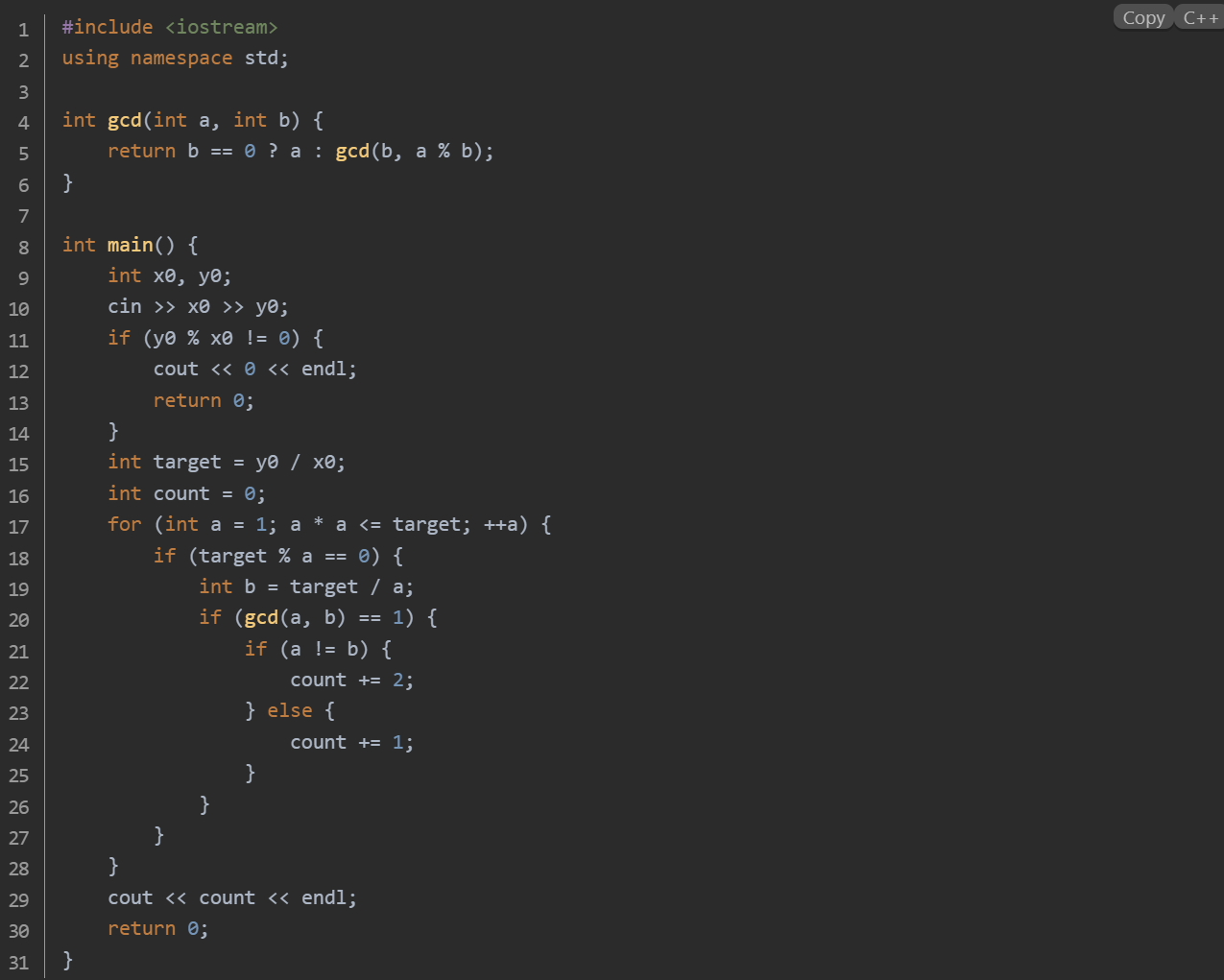
思路：根据 P * Q = gcd(P, Q) * lcm(P, Q)，设 P = a * x0、Q = b * x0（a 与 b 互质），推出 a * b = y0 / x0。读取 x0 和 y0，若 y0 不能被 x0 整除，直接输出 0 并结束。计算 target = y0 / x0，枚举 target 的因数对 (a, b)，用 gcd 函数判断 a 和 b 是否互质。若 a 与 b 互质，a != b 时 count 加 2，否则加 1。输出 count。


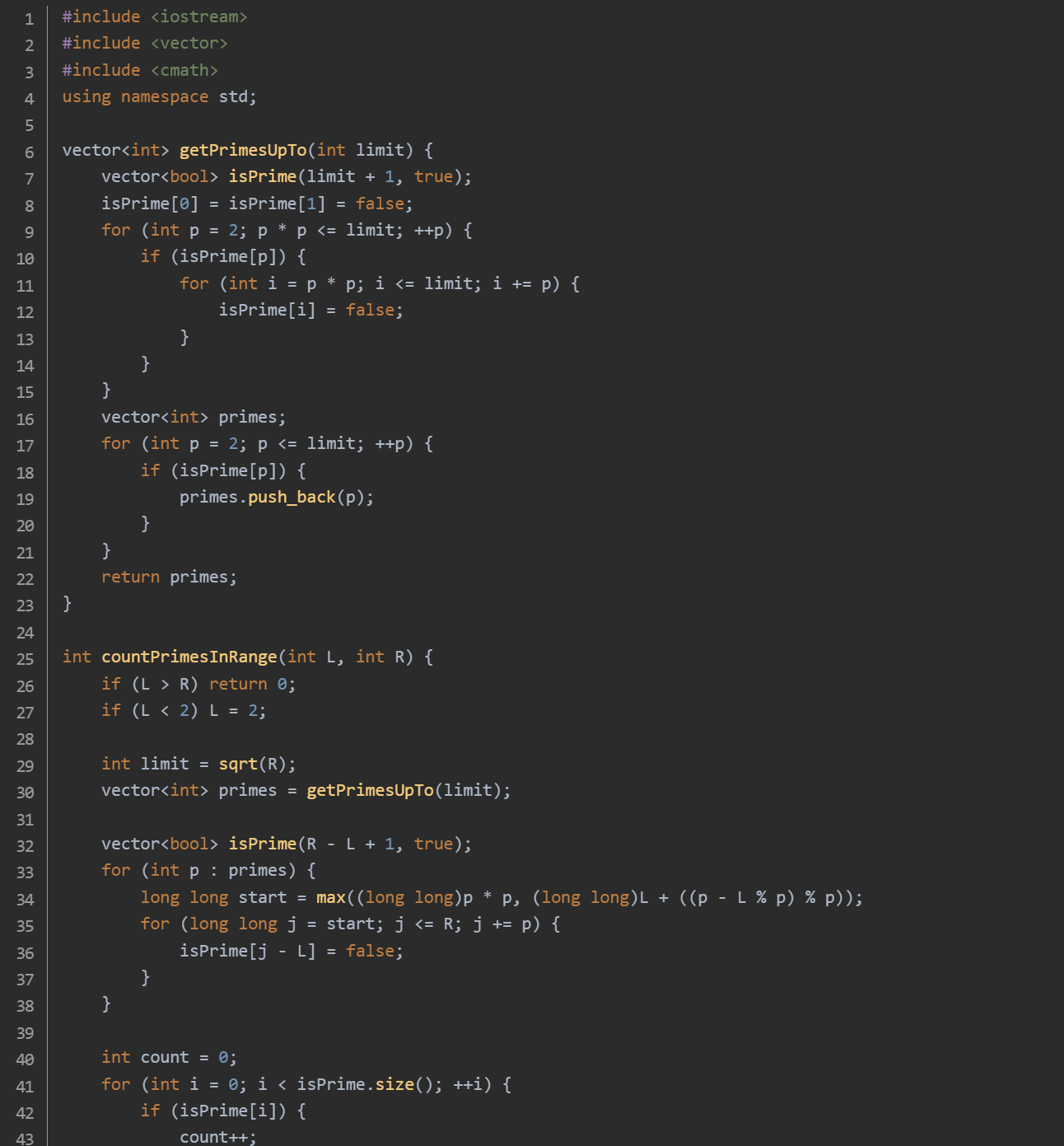
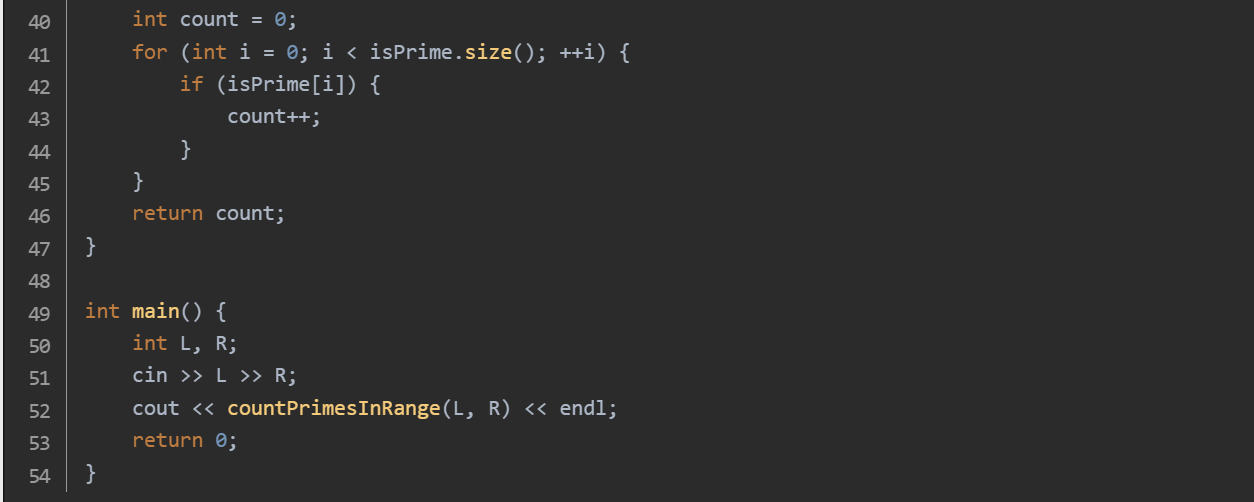
思路：使用埃拉托斯特尼筛法找到所有小于等于R的素数。countPrimesInRange 函数：初始化一个布尔数组 isPrime，表示区间 [𝐿,𝑅]内的数是否为素数。对于每个预处理得到的素数p，从L开始找到第一个能被 p整除的数，然后标记所有p的倍数为合数。最后统计 isPrime 数组中为 true 的个数。主函数：读取输入的L和R，调用 countPrimesInRange 函数并输出结果。

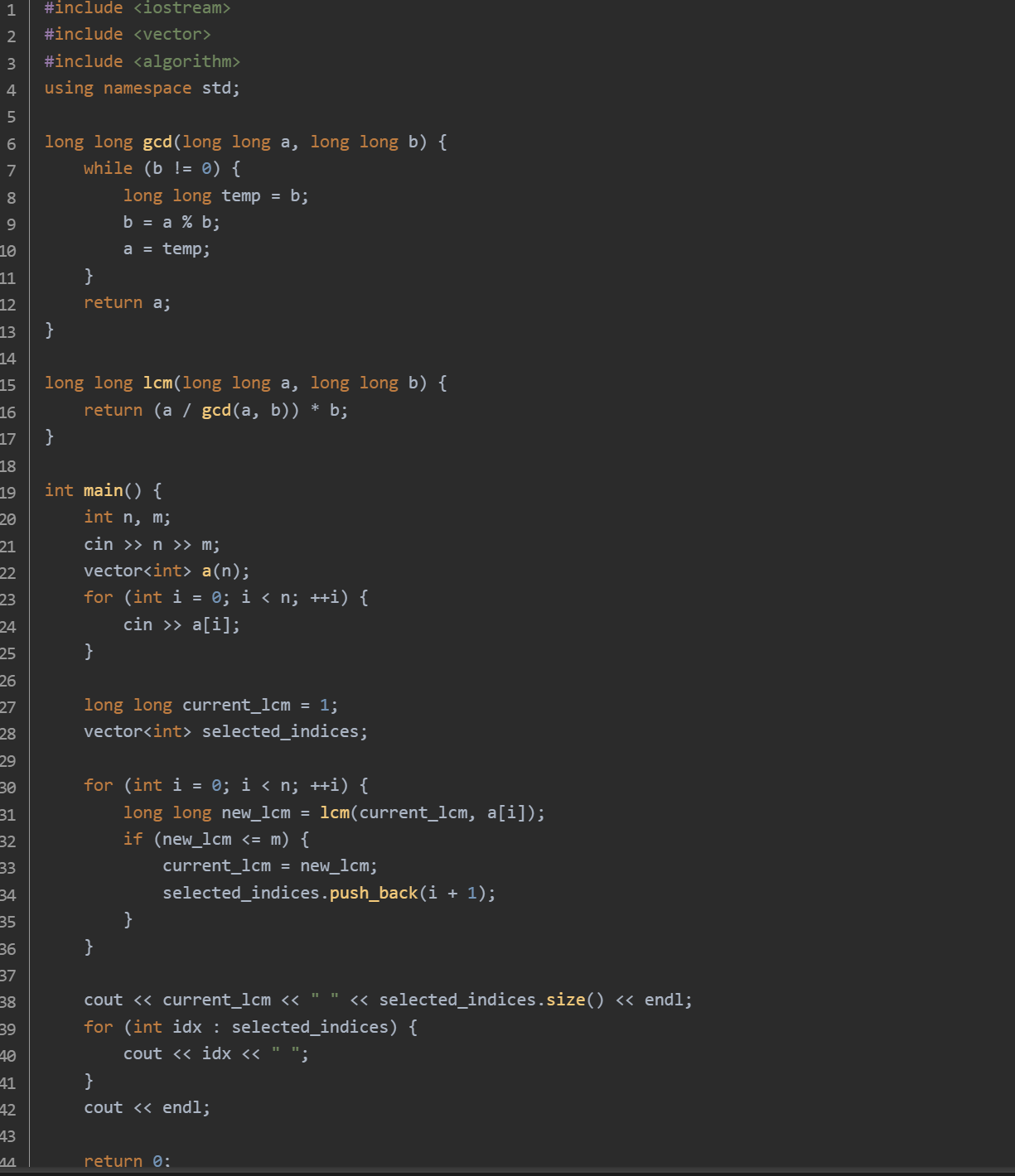
思路：gcd 函数：计算两个数的最大公约数（GCD）。lcm 函数：计算两个数的最小公倍数（LCM）。主函数读取输入的n和m读取数组a。初始化当前 LCM 为 1，并创建一个空列表 selected_indices 来存储选中的元素位置。遍历数组，计算新的LCM，如果不超过m，则将该元素加入子序列。输出最终的 LCM 和子序列的长度，以及子序列中元素的位置。

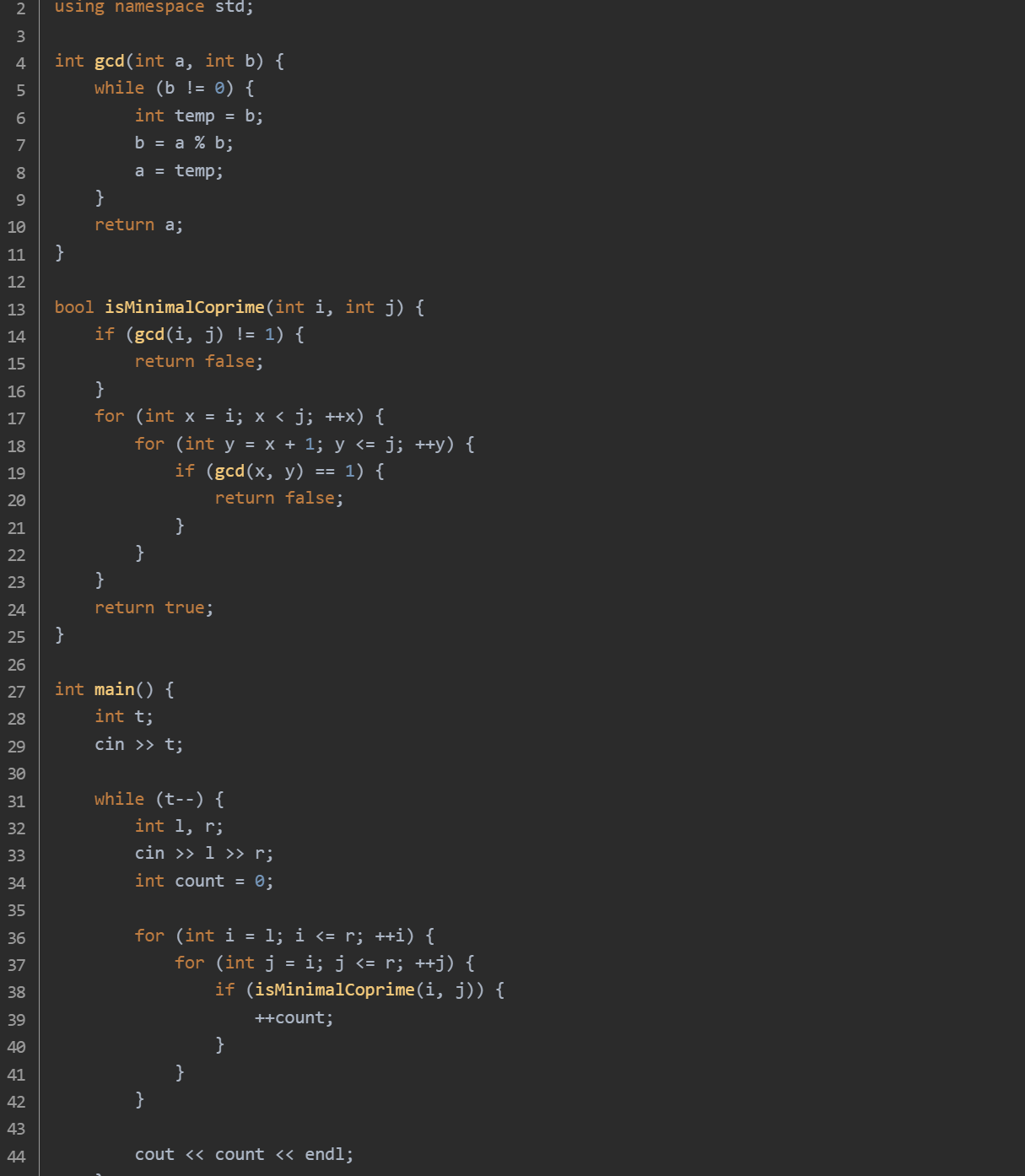
思路：gcd 函数：该函数用于计算两个整数的最大公约数，采用欧几里得算法实现。isMinimalCoprime 函数：该函数用于判断区间 [i, j] 是否为最小互质区间。首先检查 i 和 j 的最大公约数是否为 1，如果不是，则该区间不是互质区间，返回 false。然后检查 [i, j] 内是否包含其他互质区间，通过两层循环枚举所有可能的子区间 [x, y]（其中 i <= x < y <= j），如果存在一个子区间是互质的，则 [i, j] 不是最小互质区间，返回 false。如果以上条件都不满足，则 [i, j] 是最小互质区间，返回 true。main 函数：读取测试用例的数量 t。对于每个测试用例，读取区间 [l, r]。通过两层循环枚举所有可能的子区间 [i, j]（其中 l <= i <= j <= r），对于每个子区间，调用 isMinimalCoprime 函数进行判断，如果是最小互质区间，则计数器 count 加 1。


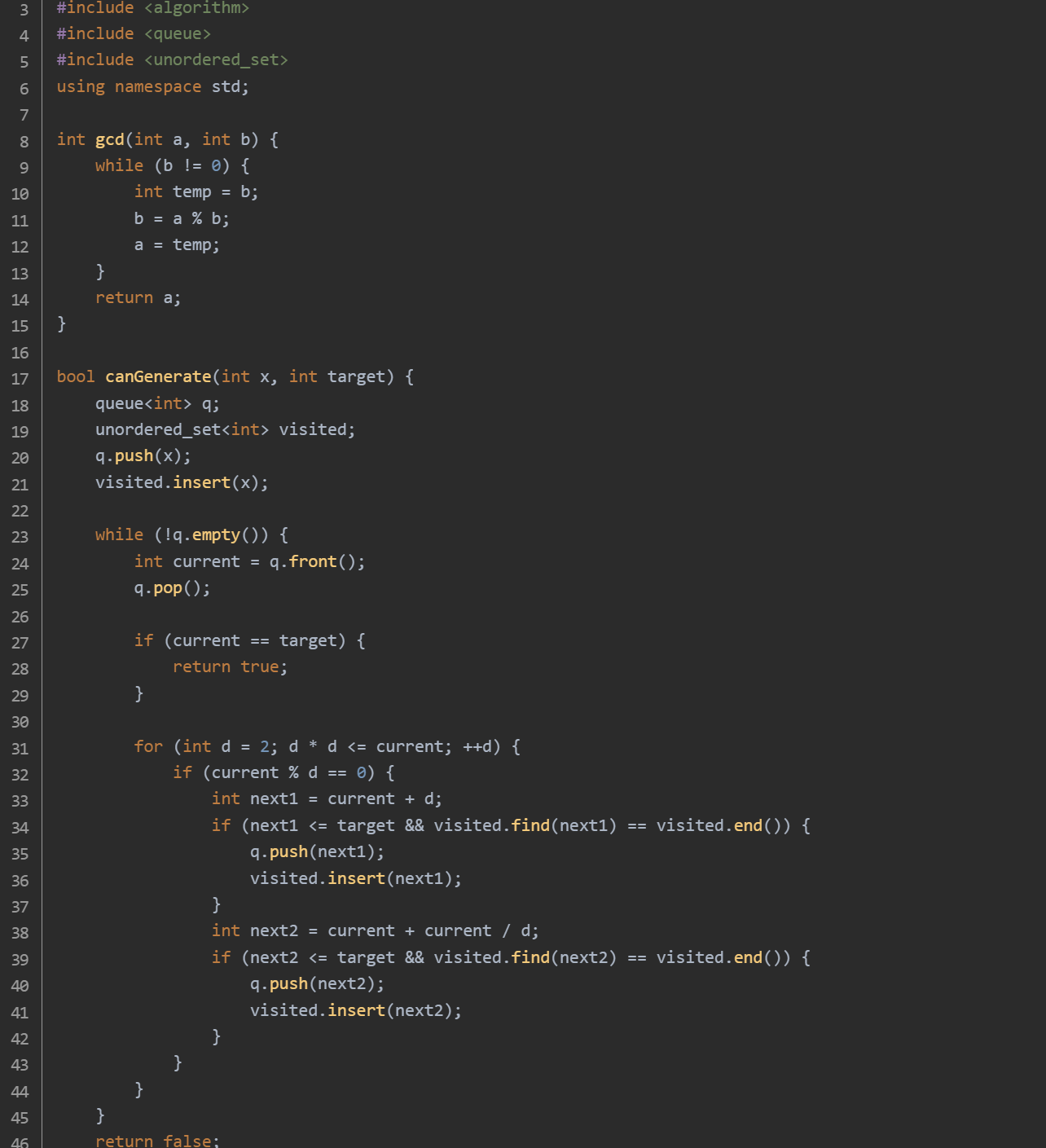
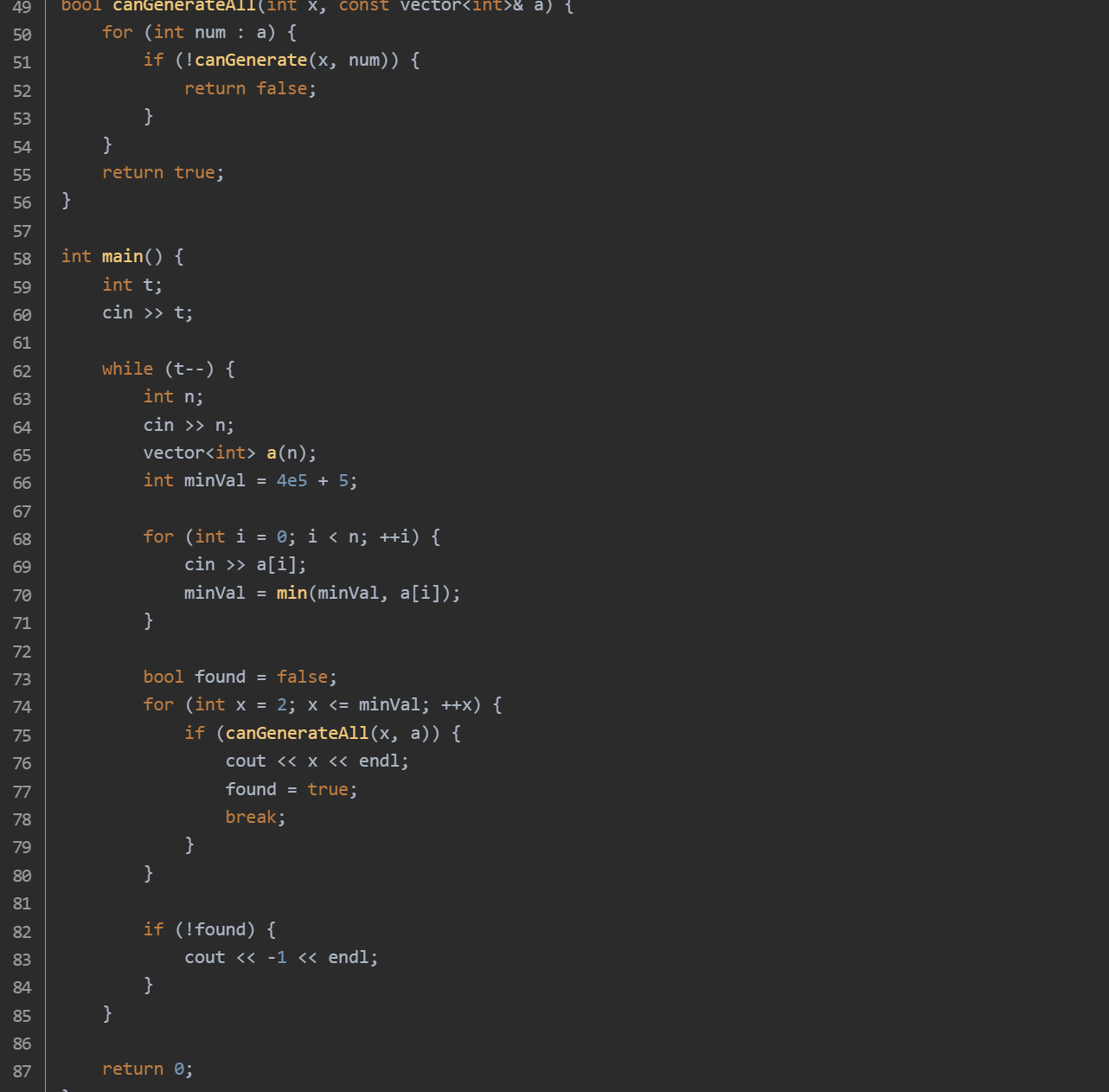
思路：gcd 函数：该函数使用欧几里得算法计算两个整数的最大公约数。canGenerate 函数：使用广度优先搜索（BFS）来判断 x 是否能生成 target。利用队列 q 存储待处理的数，使用 unordered_set 存储已经访问过的数，避免重复处理。对于当前数 current，找出其所有不小于 2 的除数 d，计算 current + d 和 current + current / d，如果这些数不超过 target 且未被访问过，则加入队列和已访问集合。如果在搜索过程中到达了 target，则返回 true，否则返回 false。canGenerateAll 函数：遍历数组 a，对于每个元素 num，调用 canGenerate 函数检查 x 是否能生成 num。如果有任何一个元素不能生成，则返回 false，否则返回 true。main 函数：读取测试用例的数量 t。对于每个测试用例，读取数组的长度 n 和数组 a 的元素，并找出数组中的最小元素 minVal。从 2 到 minVal 遍历所有可能的 x，对于每个 x，调用 canGenerateAll 函数进行检查。如果找到一个 x 能生成数组中的所有元素，则输出 x 并标记为已找到，然后跳出循环。如果遍历完所有可能的 x 都没有找到合适的，输出 -1。
学习总结：
1.最大公约数（GCD）定义：两个或多个整数共有约数中最大的一个。欧几里得算法：通过反复应用 gcd(a, b) = gcd(b, a % b) 直到 b 为 0，此时 a 即为最大公约数。如代码中常见的 int gcd(int a, int b) { while (b != 0) { int temp = b; b = a % b; a = temp; } return a; }。在判断两个数是否互质（gcd(a, b) == 1 时，a 和 b 互质）、求解同余方程有解条件、计算最小公倍数（lcm(a, b) = a * b / gcd(a, b)）等方面都有重要应用。
2.最小公倍数（LCM）定义：两个或多个整数公有的倍数中最小的一个。利用公式 lcm(a, b) = a * b / gcd(a, b) 进行计算，可通过先求出最大公约数再计算最小公倍数。在处理数组子序列相关问题时，计算子序列元素的最小公倍数，用于筛选符合条件的子序列。
3.同余方程
定义：形如 ax ≡ b (mod m) 的方程，其中 a、b、m 为已知整数，x 为未知数。
求解方法：使用扩展欧几里得算法求解 ax + my = gcd(a, m) 的一组整数解 (x0, y0)，然后根据同余方程有解的充要条件（b 能被 gcd(a, m) 整除）判断方程是否有解。若有解，可通过对解进行适当变换得到最小非负整数解。解决一些需要在模运算下求解方程的实际问题。
4.素数相关
素数定义：一个大于 1 的自然数，除了 1 和它自身外，不能被其他自然数整除的数。素数筛选法：埃拉托斯特尼筛法：用于找出一定范围内的所有素数。其基本思想是从 2 开始，将每个素数的倍数标记为合数，逐步筛选出素数。在处理区间 [L, R] 内素数统计问题时，可先预处理出小于等于 R 的素数，再对区间内的数进行标记和统计。素数相关的计数问题、密码学等领域。
5.区间与互质问题
互质区间：区间 [l, r] 中 l 和 r 互质（即 gcd(l, r) == 1）的区间。
最小互质区间：不包含任何不等于它本身的互质区间的互质区间。判断一个区间是否为最小互质区间，需要先判断其是否为互质区间，再检查其内部是否包含其他互质区间。
应用场景：区间筛选和计数问题。