2.7

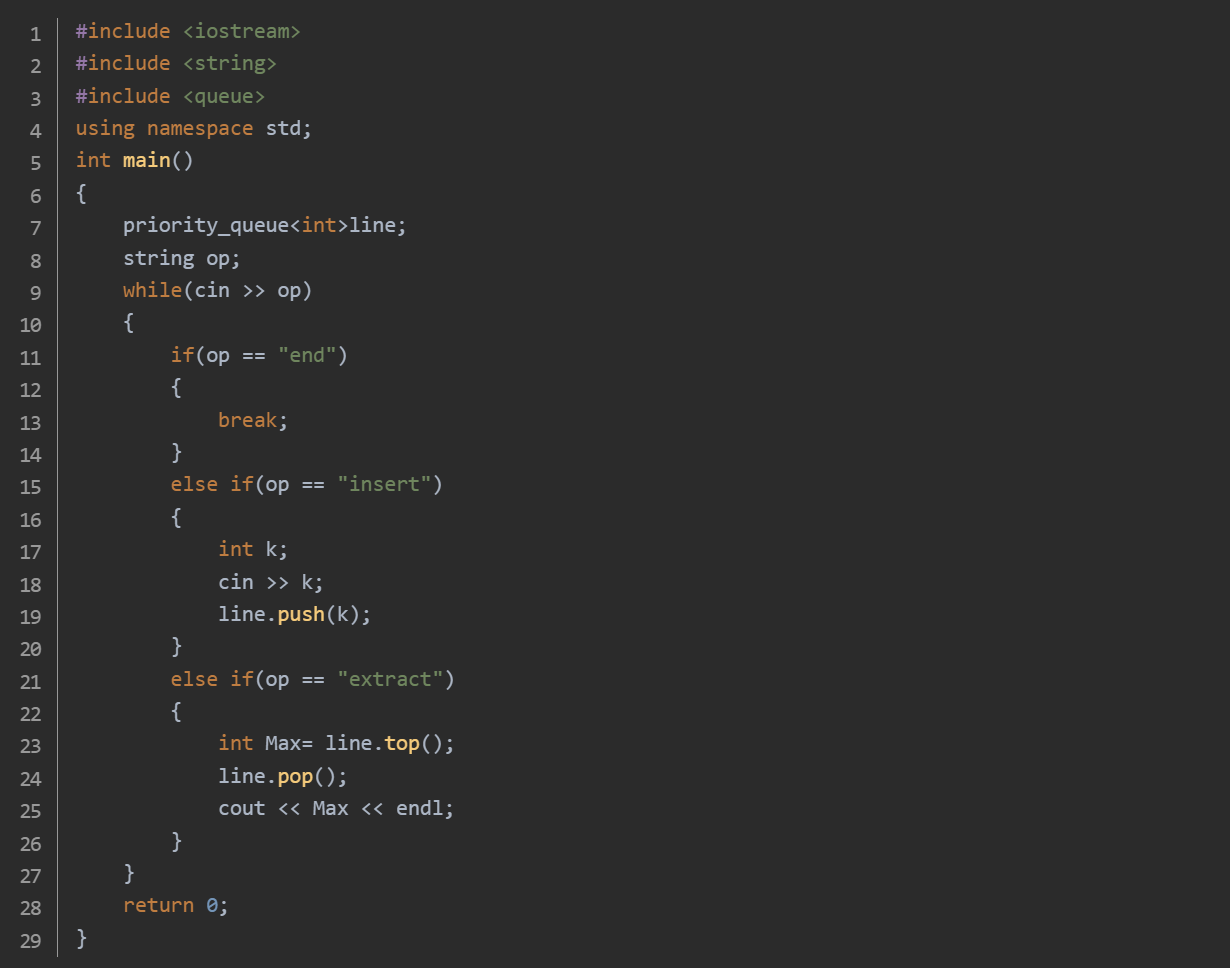
思路：使用 while(cin >> op) 不断从标准输入读取操作命令，该循环会持续执行，直到输入结束或者满足跳出条件。若读取到的命令为 "end"，则使用 break 语句跳出循环，结束程序的操作处理流程。当读取到的操作命令为 "insert" 时：继续从标准输入读取一个整数 k。调用优先队列的 push 方法，将 k 插入到优先队列 line 中。插入操作会自动调整队列结构，保证队首元素始终是队列中的最大值。当读取到的操作命令为 "extract" 时：调用优先队列的 top 方法获取队首元素（即最大元素），并将其赋值给变量 Max。调用优先队列的 pop 方法将队首元素从队列中移除。使用 cout 将提取出的最大元素 Max 输出到标准输出，并换行。当循环结束后，main 函数返回 0，表示程序正常结束。


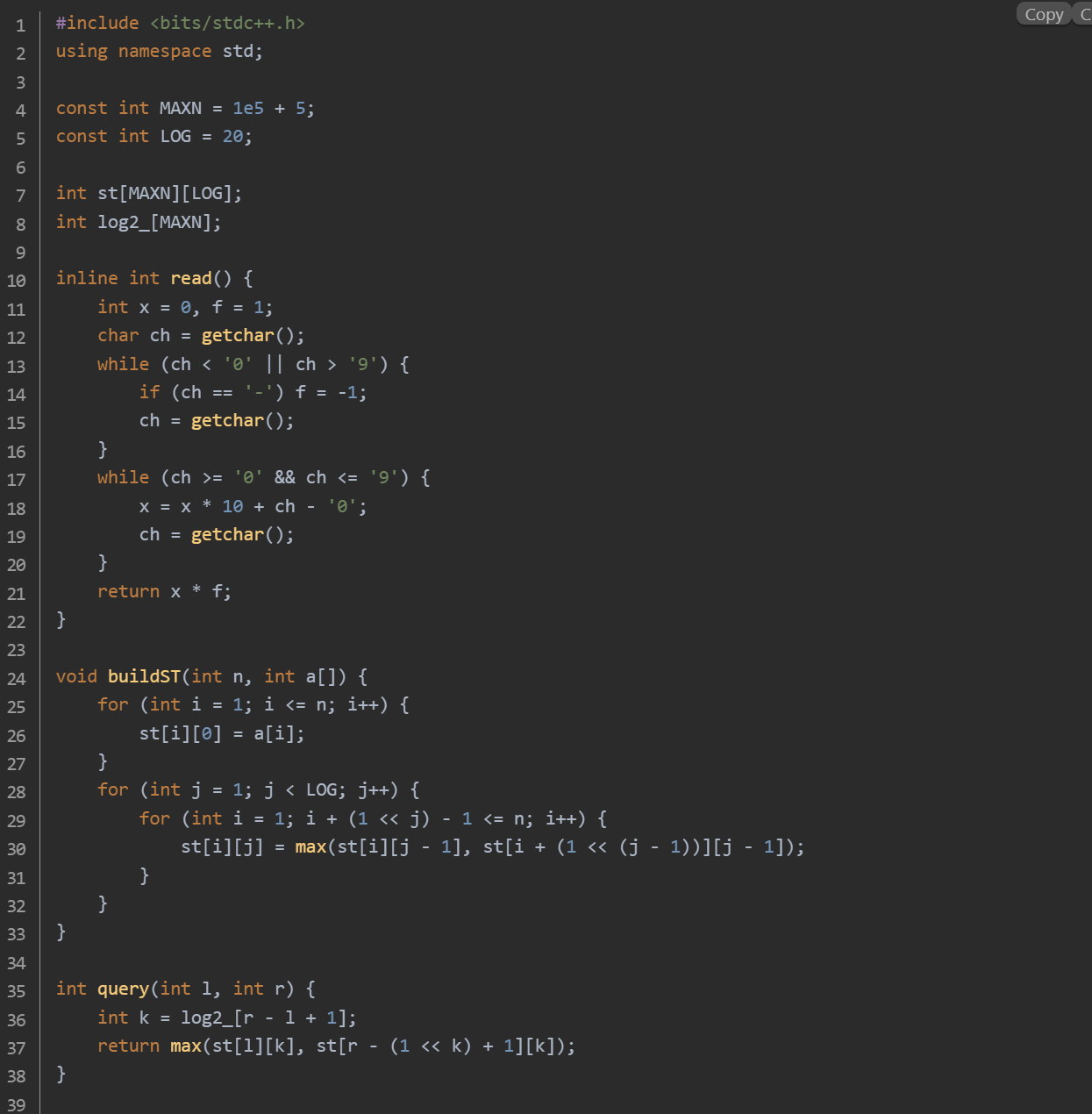
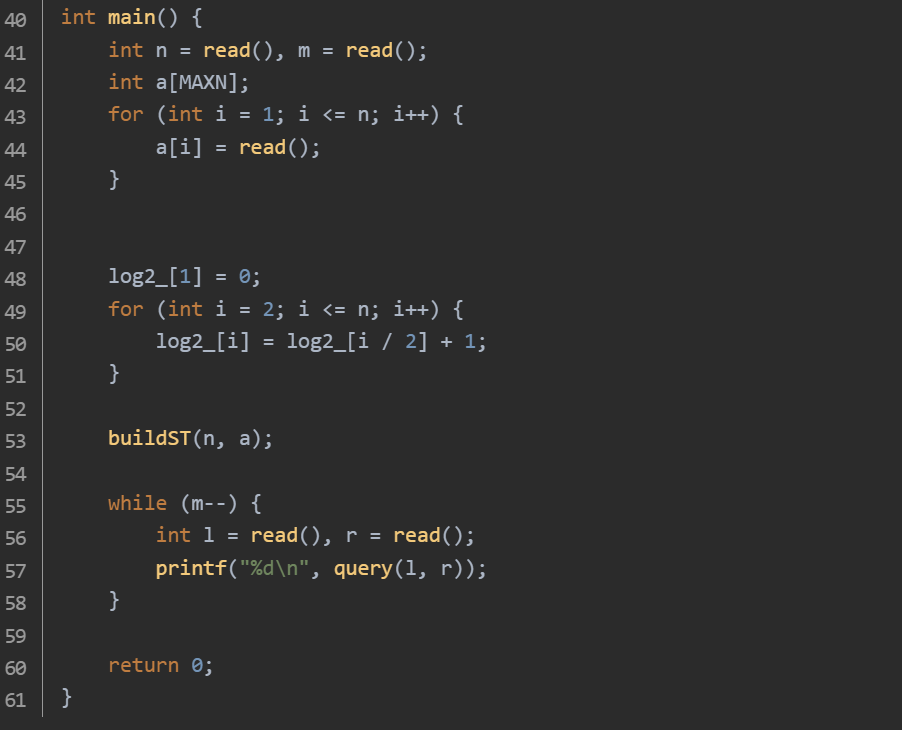
思路：自定义 read 函数加快数据输入速度。计算每个数对应的以 2 为底的对数并存储在 log2_ 数组。构建 ST 表 st，st[i][j] 表示从第 i 个元素开始长度为 的区间内的最大值。对于每次查询的区间 [l, r]，借助 log2_ 数组找到合适的 ，通过两个重叠区间的最大值得到结果。

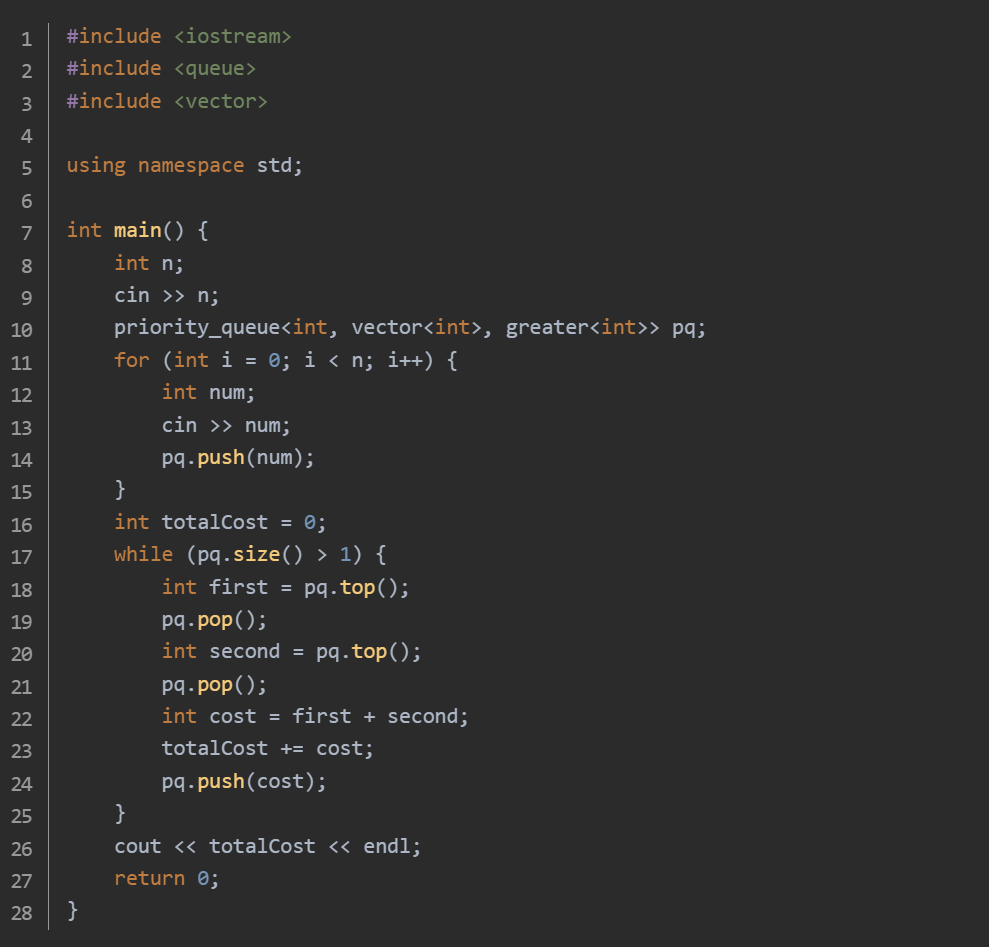
思路：读取果子种类数 n，并将每种果子数目读入最小堆优先队列 pq。当队列元素数大于 1 时，取出最小的两堆果子合并，合并消耗体力累加到 totalCost，合并后的新堆再入队。输出合并所有果子的最小体力耗费值 totalCost。

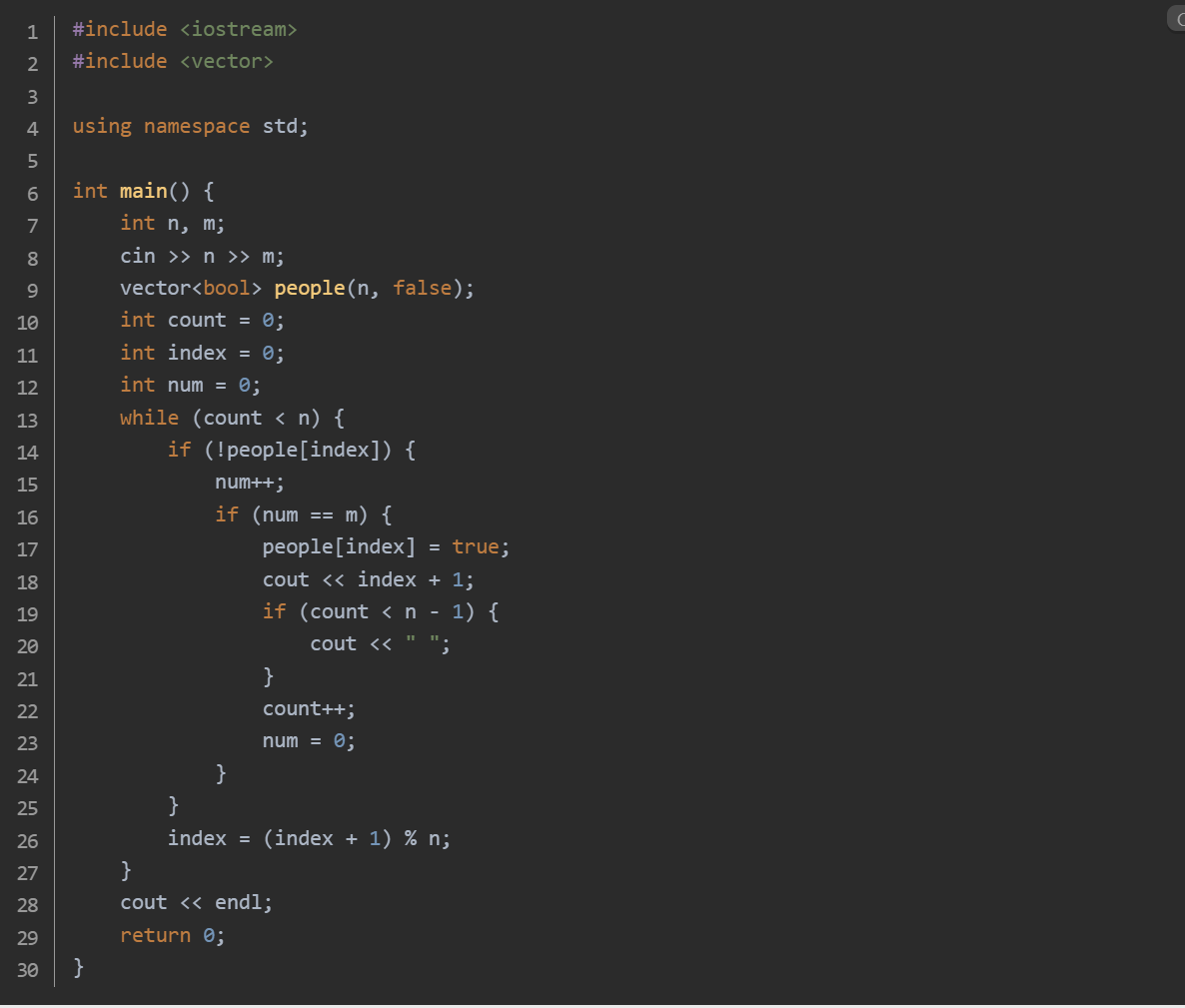
思路：读取人数 n 和报数 m，用布尔数组标记人员是否出圈，初始都未出圈，同时初始化出圈人数、当前报数人索引和报数。持续循环，当未出圈人数大于 0 时，对未出圈的人报数，报到 m 时该人出圈并输出编号，更新出圈人数和报数，最后更新报数人索引，实现循环报数。循环结束后，所有人员都已出圈，换行结束输出。

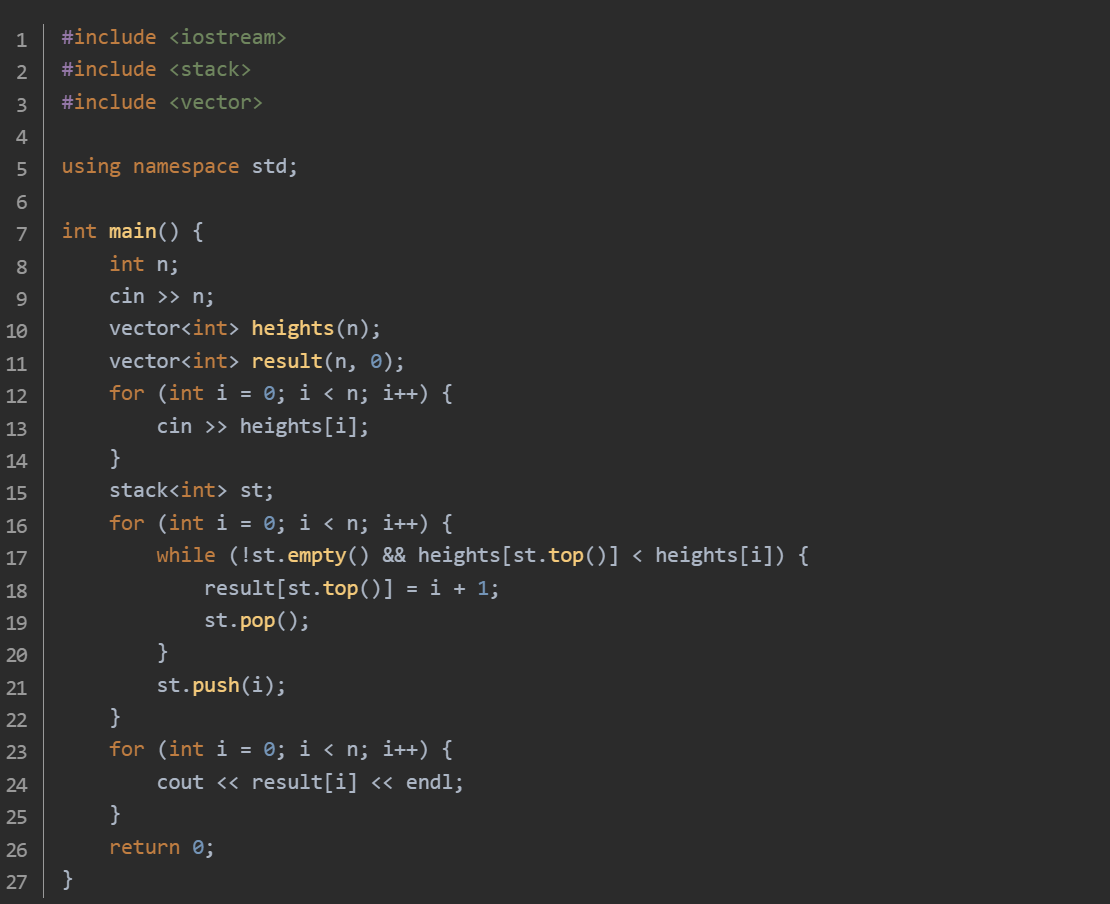
思路：读取奶牛的数量 n。用 vector heights 存储每头奶牛的身高，vector result 存储每头奶牛的最近仰望对象的编号，初始都设为 0。创建一个空的栈 st，用于辅助处理。按顺序遍历每头奶牛的身高：当栈不为空且栈顶奶牛的身高小于当前奶牛的身高时，说明栈顶奶牛找到了仰望对象（即当前奶牛），更新 result 数组中栈顶奶牛对应位置的值为当前奶牛的编号（i + 1），然后将栈顶元素弹出。当前奶牛的索引压入栈中。遍历 result 数组，依次输出每头奶牛的最近仰望对象的编号。


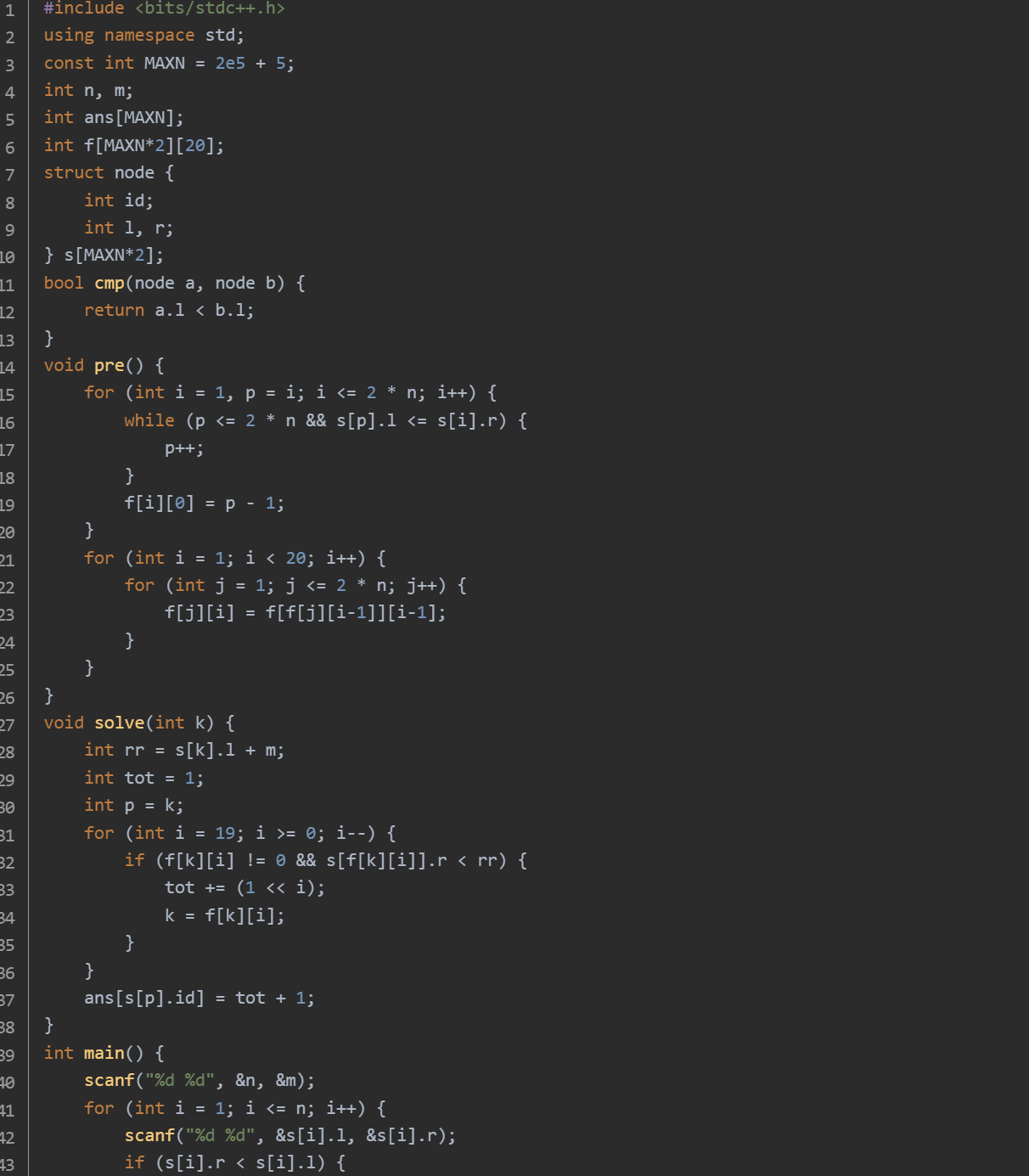
思路：读取边防战士数量 n 和边防站数量 m。读取每个战士的奔袭区间 [l, r]，若 r < l 则将 r 加上 m 使其变为连续区间，同时记录战士原始编号 id。
将所有区间按左端点排序，为处理环形问题，复制一份区间并将左右端点都加上 m。初始化 f[i][0]：使用双指针，对于每个区间 i，找到左端点不超过其右端点的最靠后的区间下标并记录到 f[i][0]。通过递推 f[j][i] = f[f[j][i - 1]][i - 1] 构建完整的倍增表，用于后续快速跳跃查找。对于每个战士对应的区间，设定目标右端点 rr 为该区间左端点加上 m。利用倍增法，从大到小尝试跳跃，若跳跃后区间右端点小于 rr 则更新当前区间并累加使用的区间数。最终结果加 1 后记录到对应战士的答案数组 ans 中。按顺序输出每个战士必须参加时所需的最少战士数量。
学习总结：1.优先队列
优先队列可实现元素按优先级排序，如最大堆或最小堆。在果子合并问题中，使用最小堆优先队列 priority_queue<int, vector, greater> 来存储果子数量，方便每次取出最小的两堆果子进行合并，降低合并的体力消耗。在优先队列操作问题里，利用最大堆优先队列存储元素，根据输入命令实现插入和提取最大元素操作。
常用操作：push（插入元素）、top（获取队首元素）、pop（移除队首元素）。
2.栈（单调栈）
单调栈是一种特殊的栈，栈内元素保持单调递增或递减。在奶牛仰望问题中，使用单调栈来寻找每头奶牛的最近仰望对象。按顺序遍历奶牛身高，若栈顶奶牛身高小于当前奶牛，说明栈顶奶牛找到了仰望对象，更新结果并弹出栈顶元素，再将当前奶牛索引入栈。
特性：能在 时间复杂度内解决一些与单调性相关的问题。
3.数组与布尔数组
数组可用于存储数据，如在奶牛仰望问题中用 vector heights 存储奶牛身高，vector result 存储每头奶牛的仰望对象编号；在约瑟夫环问题中用布尔数组 vector people 标记人员是否出圈。
布尔数组常用于标记状态，便于进行条件判断和状态更新。
4.贪心算法
贪心算法在每一步都做出当前看起来最优的选择，从而希望最终得到全局最优解。果子合并问题是贪心算法的典型应用，每次都选择最小的两堆果子合并，使得合并的总体力消耗最小。
适用场景：问题具有贪心选择性质和最优子结构性质。
5.倍增法
倍增法通过预处理和递推，利用 的特性实现快速跳跃和查询。在边防战士接力奔袭问题中，使用倍增表 f[i][j] 记录从第 i 个区间出发，经过 个区间能到达的最远区间下标。在查询时，利用倍增法从大到小尝试跳跃，快速找到覆盖目标区间所需的最少区间数。
优点：能将时间复杂度从 优化到 。
6.动态规划（ST 表构建）
动态规划通过将大问题分解为小问题，并保存小问题的解来避免重复计算。在 ST 表区间最大值查询问题中，ST 表 st[i][j] 表示从第 i 个元素开始长度为 的区间内的最大值，通过递推公式 st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]) 构建，从而实现 时间复杂度的区间最大值查询。
核心：状态定义、状态转移方程和边界条件。
7.快速读入
自定义 read 函数通过直接操作字符，避免 cin 或 scanf 可能带来的额外开销，加快数据读入速度，在处理大规模数据时能显著提升效率，如在 ST 表区间最大值查询问题中使用。
8.预处理
预处理可以减少重复计算，提高算法效率。在 ST 表问题中，预先计算以 2 为底的对数并存储在 log2_ 数组中；在边防战士接力奔袭问题中，对区间进行排序、复制和处理环形情况，并初始化倍增表 f[i][0] 等操作都属于预处理。
9.循环读取输入：使用 while(cin >> op) 等循环结构不断读取输入，根据输入的命令进行相应的操作，直到满足特定条件（如输入 end）结束循环，如优先队列操作问题。
模拟过程对于一些问题，通过模拟实际的操作过程来求解。约瑟夫环问题中，使用循环模拟人们报数和出圈的过程，根据报数情况更新人员状态和出圈顺序。