1.26

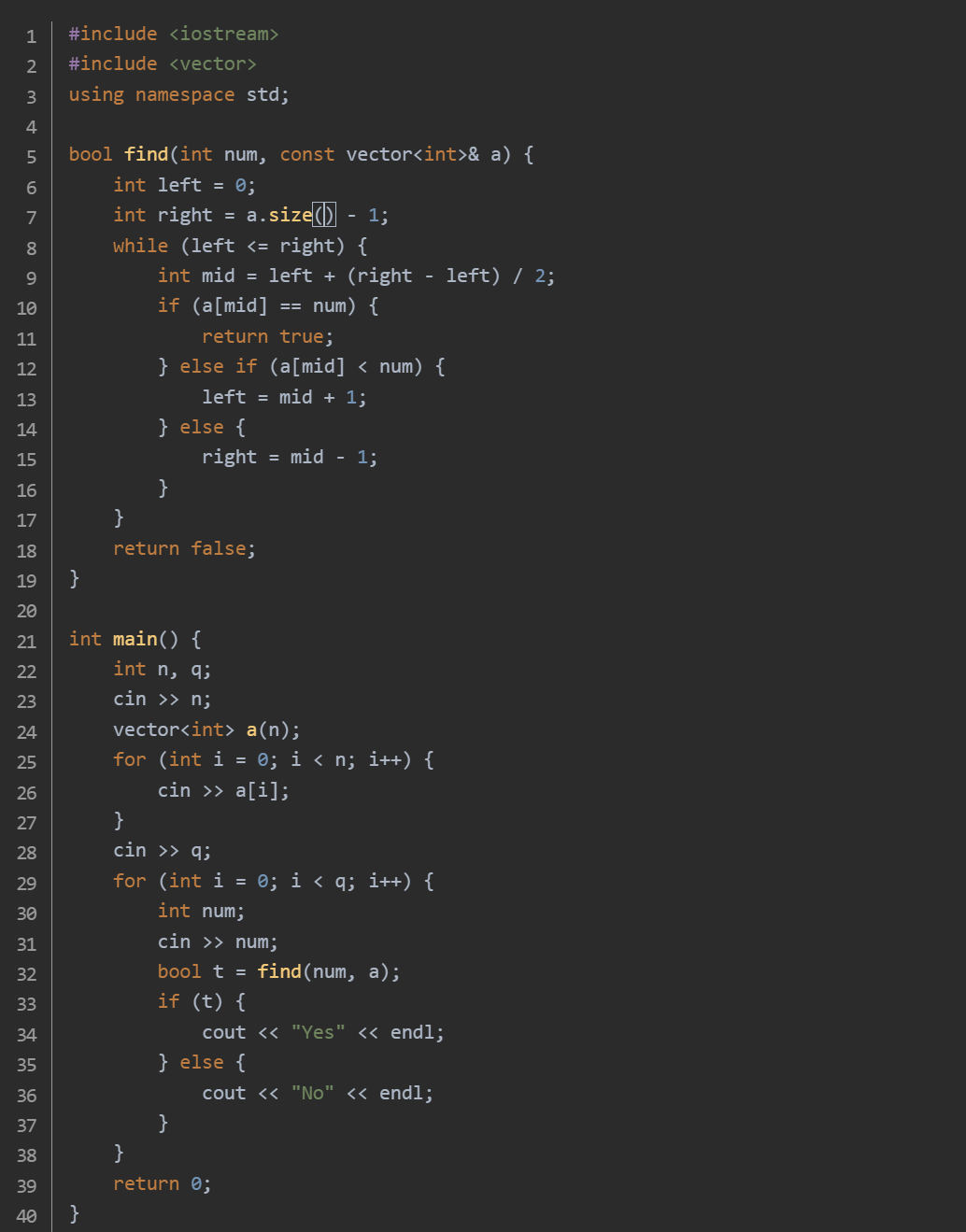
思路：find 函数用于执行二分查找操作计算中间位置 mid= left + (right - left) / 2
将中间位置的元素 a[mid] 与目标元素 num 进行比较：若 a[mid] 等于 num，说明找到了目标元素，函数返回 true。若 a[mid] 小于 num，说明目标元素在 mid 的右侧，更新 left = mid + 1，缩小查找范围到右半部分。若 a[mid] 大于 num，说明目标元素在 mid 的左侧，更新 right = mid - 1。如果循环结束后仍未找到目标元素，函数返回 false。在 main 函数的查询循环中，每次读取一个目标元素 num 后，调用 find 函数进行查找，若 t 为 true，说明目标元素存在于数组中，输出 "Yes"。若 t 为 false，说明目标元素不存在于数组中，输出 "No"。

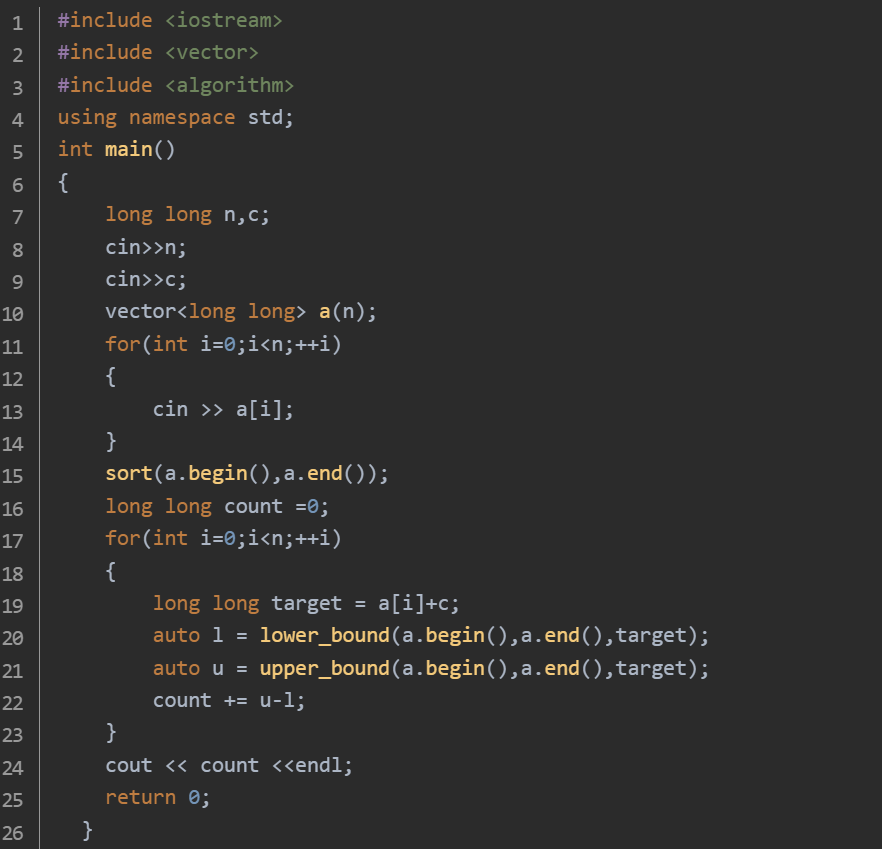
使用 sort(a.begin(), a.end()) 对数组 a 进行升序排序初始化一个变量 count 为 0，用于记录满足差值为 c 的数对数量。
遍历数组 a 中的每个元素 a[i]：计算目标值 target = a[i] + c。使用 lower_bound 函数找到数组中第一个大于等于 target 的元素 l。使用 upper_bound 函数找到数组中第一个大于 target 的元素 u。计算差值 u - l，这个差值就是数组中值等于 target 的元素的个数。将这个差值累加到 count 中。遍历完数组后，count 中存储的就是满足差值为 c 的数对数量，将其输出到标准输出。

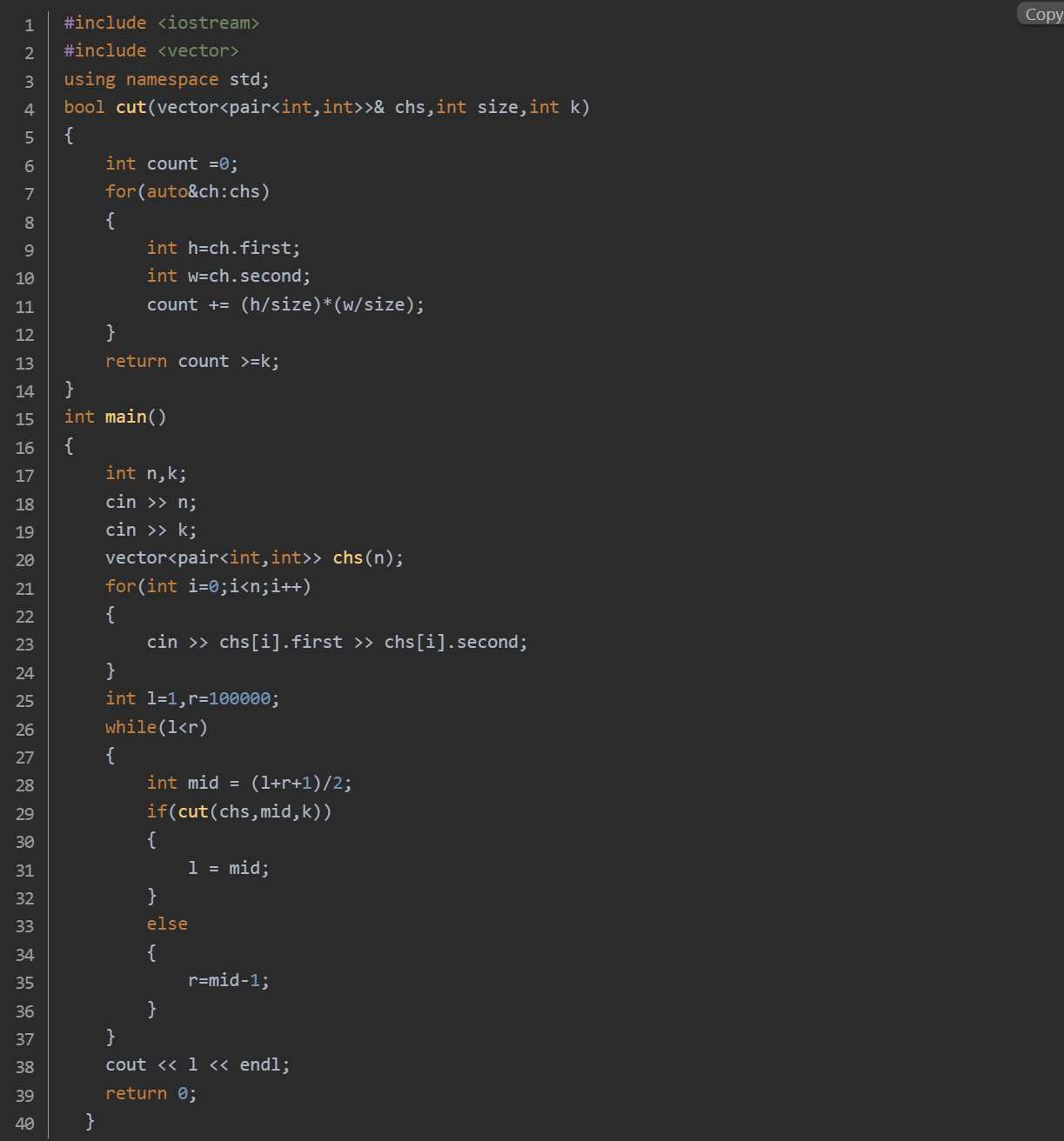
思路：创建一个长度为 n 的 vector，其中每个元素是一个 pair<int, int> 类型，用于存储每块长方形巧克力的长和宽。在 l < r 的条件下进行循环：计算中间值 mid = (l + r + 1) / 2。调用 cut 函数检查以 mid 为边长能否切出至少 k 块正方形巧克力：遍历 chs 中的每块巧克力，对于每块巧克力，计算其长和宽分别除以 size 的商，然后将这两个商相乘，得到该块巧克力能切出的边长为 size 的正方形数量。将所有巧克力能切出的正方形数量累加起来，得到总的正方形数量 count。最后判断 count 是否大于等于 k，如果是，则返回 true，表示以 size 为边长可以切出至少 k 块正方形巧克力；否则返回 false。根据 cut 函数的返回结果更新二分查找的边界：如果以 mid 为边长可以切出至少 k 块正方形巧克力，说明可以尝试更大的边长，将左边界 l 更新为 mid。如果以 mid 为边长不能切出至少 k 块正方形巧克力，说明需要尝试更小的边长，将右边界 r 更新为 mid - 1。当 l 不再小于 r 时，二分查找结束，此时 l 即为能切出至少 k 块正方形巧克力的最大边长，将其输出。

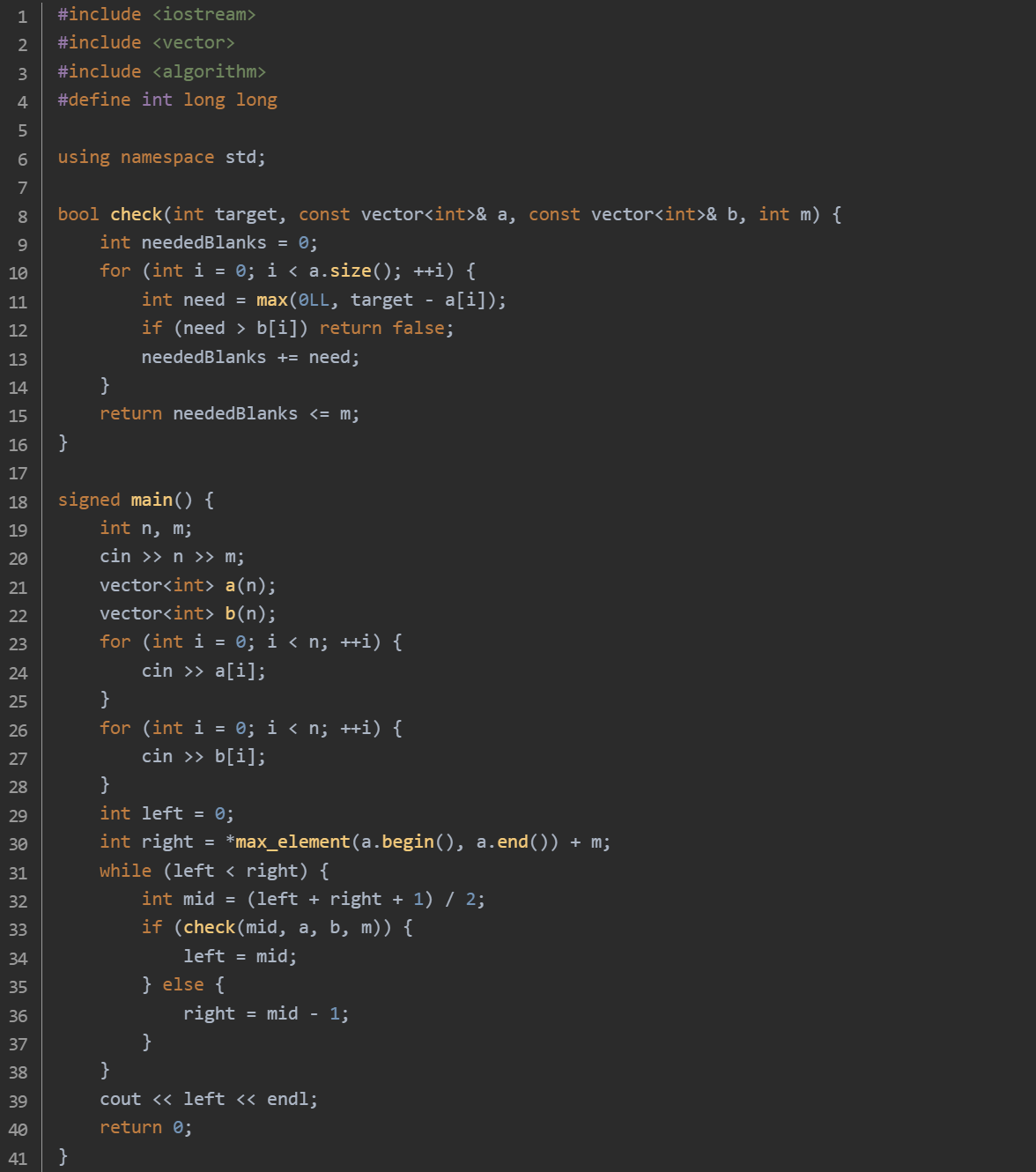
设定二分查找的左边界 left 为 0，这是可能凑出的最小套牌数量。设定右边界 right 为现有卡牌最大数量加上空白牌数量，即 *max_element(a.begin(), a.end()) + m，这是可能凑出的最大套牌数量。
在 left < right 的条件下进行循环：计算中间值 mid = (left + right + 1) / 2/.调用 check 函数检查是否能凑出 mid 套牌：对于每种卡牌 i，计算为了凑出 mid 套牌，该种卡牌还需要的数量 need = max(0LL, mid - a[i])。如果 mid 小于等于 a[i]，则 need 为 0；否则，need 为 mid - a[i]。检查 need 是否超过了该种卡牌可手写的最大数量 b[i]，如果超过则无法凑出 mid 套牌，函数返回 false。累加所有卡牌所需的额外数量到 neededBlanks 中。最后检查 neededBlanks 是否超过了空白牌的总数 m，如果超过则无法凑出 mid 套牌，函数返回 false；否则返回 true。根据 check 函数的返回结果更新二分查找的边界：如果能凑出 mid 套牌，说明可以尝试更大的套牌数量，将左边界 left 更新为 mid。如果不能凑出 mid 套牌，说明需要缩小套牌数量，将右边界 right 更新为 mid - 1。当 left 不再小于 right 时，二分查找结束，此时 left 即为最多能凑出的套牌数量，将其输出。


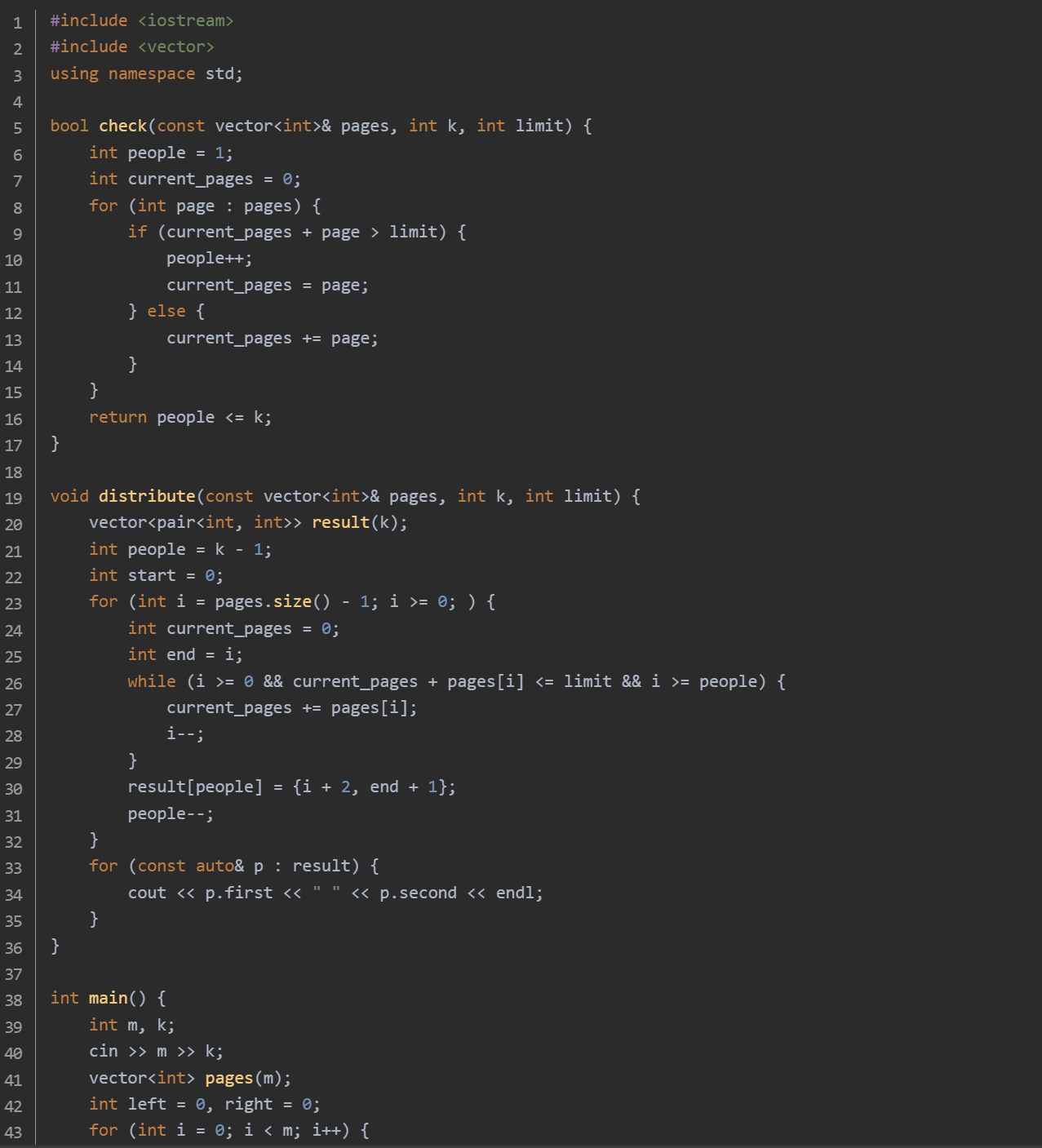
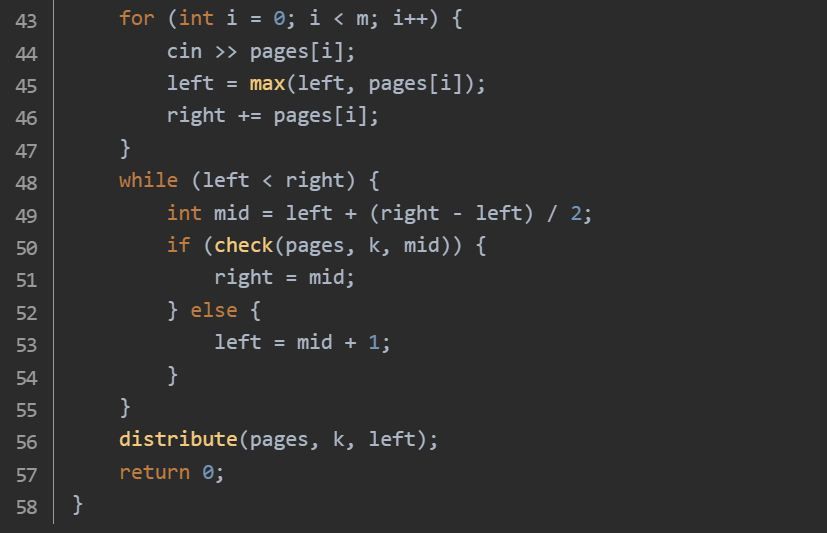
思路：创建一个长度为 m 的 vector 容器 pages，用于存储每本书的页数。通过循环依次读取每本书的页数并存储到 pages 中。同时，在读取过程中，确定二分查找的左右边界：左边界 left 初始化为所有书中页数的最大值，右边界 right 初始化为所有书的总页数。使用一个 while 循环进行二分查找，条件是 left < right：
计算中间值 mid，调用 check 函数来判断以 mid 作为最大抄写页数时，是否可以在 k 个人内完成所有书的抄写：在 check 函数中，初始化 people 为 1 表示当前是第 1 个人，current_pages 为 0 表示当前这个人已抄写的页数。遍历 pages 中的每本书的页数，若 current_pages + page > limit（即当前人抄写当前书后会超过最大页数限制），则需要增加一个人（people++），并将 current_pages 重置为当前书的页数；否则，将当前书的页数累加到 current_pages 中。最后判断 people 是否小于等于 k，如果是，则说明以 mid 作为最大抄写页数是可行的，返回 true；否则返回 false。根据 check 函数的返回结果更新二分查找的边界。当二分查找结束后，left 即为最小的最大抄写页数。调用 distribute 函数来确定每个人抄写的书的起始编号和终止编号：创建一个长度为 k 的 vector 容器 result，用于存储每个人抄写的书的起始和终止编号。从后往前遍历书：初始化 current_pages 为 0 表示当前人已抄写的页数，end 为当前遍历到的书的编号。只要满足 i >= 0（还没遍历完所有书）、current_pages + pages[i] <= limit（当前人抄写当前书不会超过最大页数限制）以及 i >= people（要保证剩下的人至少能分到一本书），就将当前书的页数累加到 current_pages 中，并将 i 减 1。确定当前人抄写的书的范围为 {i + 2, end + 1}，因为数组下标从 0 开始，而书的编号从 1 开始，所以要加 1。将这个范围存储到 result 中，并将人员编号减 1。最后遍历 result 容器，输出每个人抄写的书的起始编号和终止编号。

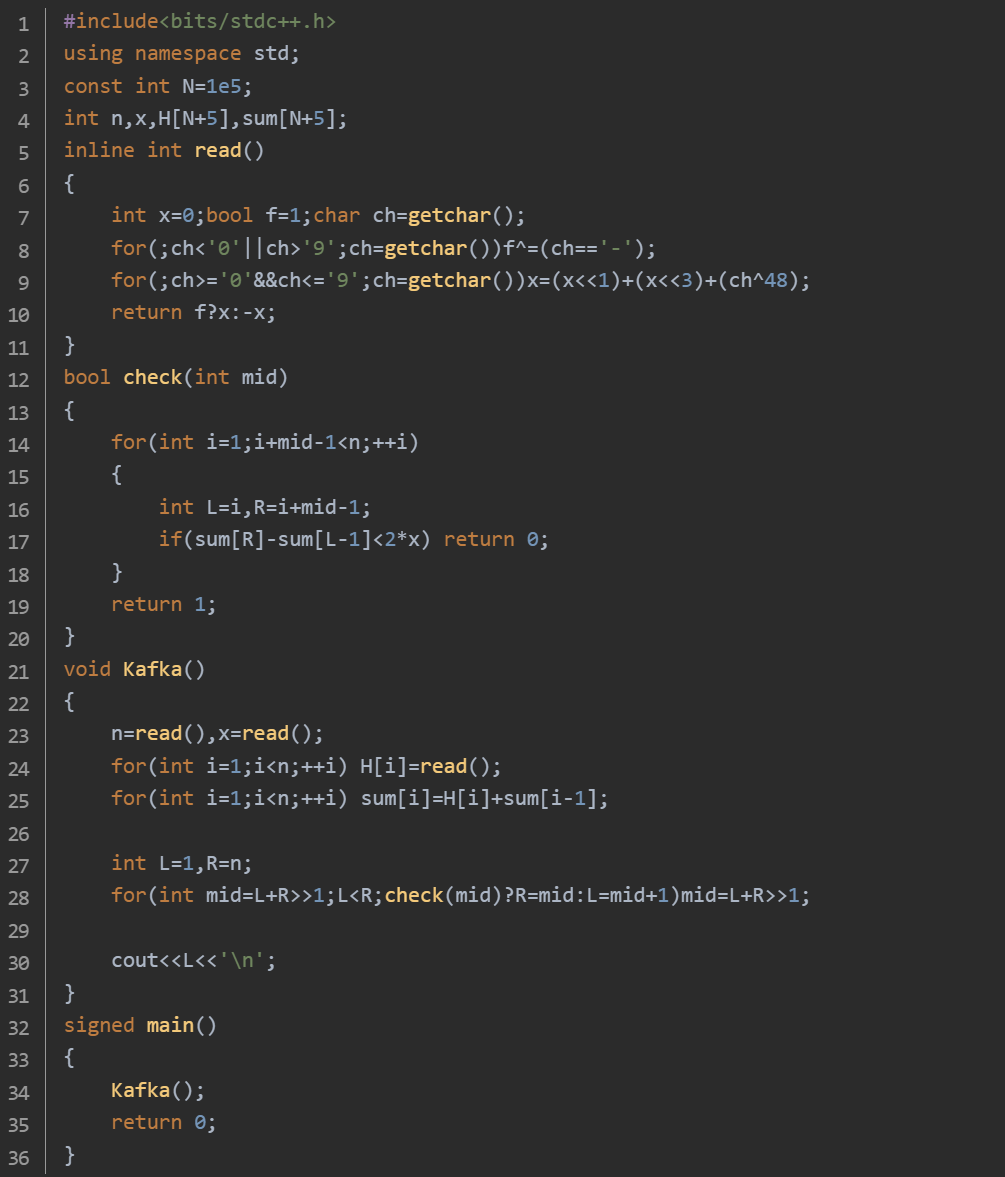
思路：初始化二分查找的左边界 L = 1，因为最小跳跃能力至少为 1；右边界 R = n，最大跳跃能力不会超过河的宽度。二分查找循环：在 L < R 的条件下进行循环，每次取中间值 mid = (L + R) >> 1（等同于 (L + R) / 2）作为当前尝试的跳跃能力。调用 check 函数检查以 mid 为跳跃能力是否满足往返 2x 次的条件。check 函数逻辑：遍历所有长度为 mid 的区间，对于每个区间 [L, R]（其中 L = i，R = i + mid - 1），计算该区间内石头的总高度 sum[R] - sum[L - 1]。如果存在某个区间的石头总高度小于 2x，说明在这个区间内的石头无法支撑往返 2x 次，返回 false。若所有区间都满足条件，则返回 true。根据 check 函数的返回结果更新二分查找的边界：若 check(mid) 返回 true，说明 mid 可能过大，更新 R = mid，尝试更小的跳跃能力。若 check(mid) 返回 false，说明 mid 过小，更新 L = mid + 1，尝试更大的跳跃能力。当 L 不再小于 R 时，二分查找结束，此时 L 即为满足往返 2x 次要求的最小跳跃能力，将其输出。
学习总结
一、二分查找算法的核心思想与应用
通过不断将搜索区间一分为二，逐步缩小查找范围，从而快速定位目标元素或满足特定条件的值。上述题目中多次运用二分查找解决不同类型的问题，总结其一般步骤如下：
确定查找范围：明确问题中可能的取值范围，分别设定左边界和右边界。例如在查找满足条件的最小跳跃能力问题中，左边界通常设为最小可能值（如 1），右边界设为最大可能值（如河的宽度 n）。
计算中间值：在每次循环中，计算当前查找区间的中间值 mid。为避免整数溢出，常使用 mid = left + (right - left) / 2 或 mid = (left + right + 1) / 2 的方式计算。
检查中间值是否满足条件：编写一个检查函数（如 check 函数），判断以 mid 作为当前尝试值时是否满足问题的条件。这一步需要根据具体问题进行逻辑设计，如在巧克力切割问题中，判断以 mid 为边长能否切出至少 k 块正方形巧克力。
更新查找范围：根据检查函数的返回结果，更新左边界或右边界。如果中间值满足条件，说明可能存在更小（或更大）的满足条件的值，相应地缩小右边界（或增大左边界）；如果不满足条件，则扩大左边界（或缩小右边界）。
结束条件：当左边界不再小于右边界时，二分查找结束，此时左边界（或右边界）即为所求的结果。
二、前缀和数组的使用
通过构建前缀和数组 sum，可以在 时间内计算出数组中任意区间 [L, R] 的元素和，即 sum[R] - sum[L - 1]。在一些需要频繁查询区间和的问题中，使用前缀和数组可以显著提高算法的效率。例如在小青蛙过河问题中，通过前缀和数组快速计算出每个长度为 mid 的区间内石头的总高度，从而判断是否满足往返次数的要求。
三、区间检查与贪心策略
在部分问题中，需要对特定长度的区间进行检查，判断是否满足一定的条件。例如在火车运货问题、书籍分配问题等中，都需要遍历所有可能的区间，检查区间内的元素总和是否满足要求。同时，在一些问题中还运用了贪心策略，如在书籍分配问题中，从后往前分配书籍，优先让后面的人承担更多的任务，以保证前面的人尽量少抄写，满足题目中 “尽可能让前面的人少抄写” 的要求。
四、代码实现技巧
快速读入函数：在处理大规模输入时，使用快速读入函数（如 read 函数）可以提高输入效率，减少程序运行时间。
STL 库的使用：例如使用 sort 函数对数组进行排序，使用 lower_bound 和 upper_bound 函数进行二分查找，使用 vector 容器存储数据等。