离散数学笔记（二）命题【更

命题概念

基础概念

  具有确切真值的陈述句是命题，命题只有真假和两种

  用带或不带下标的英文字母表示命题

原子命题和符合命题

  原子命题是不可拆分的命题，原子命题通过连接词连接成为复合命题

连接词

1. 否定联结词 \({\neg}\)

2. 合取联结词 \({\wedge}\)

3. 析取联结词 \({\vee}\)

4. 蕴含联结词 \({\to}\)：\({P \to Q}\) (前件 \({\to}\) 后件)

   善意推定：P为假但是没有证据证明Q为真，那么命题仍旧为真，前件和后件可能完全没有逻辑关系

5. 等价联结词：\({\leftrightarrow}\)

命题公式

  命题变元本身是一个公式，那么它就是命题公式（原子合式公式），使用联结词连接命题公式得到的新公式也是命题公式

  通常使用二元树表达命题公式，叶节点是原子公式，其他节点是联结词

  解释：命题公式的每一个命题变元的真值组成一个解释，记为l，如果使得命题公式为真，那么是成真赋值，否则为成假赋值。

分类

1. 永真公式，重言式：所有解释都使得公式为真

2. 永假公式，矛盾式：所有解释都使得公式为假

3. 可满足公式：有解释使得公式为真

等价

  设G H是两个命题公式，如果每一种解释，G和H的真值都相同，那么G H等价 \({G=H}\) 或 \({G \Leftrightarrow H}\)

等价关系

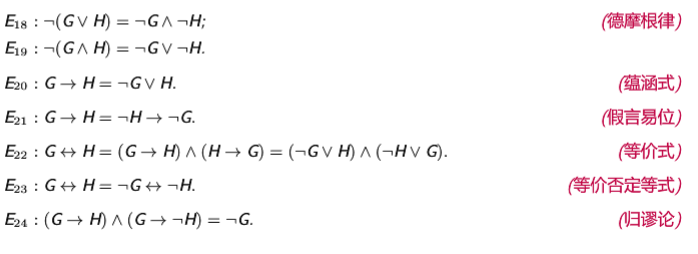
范式

  文字：命题变元或命题变元的否定，p和\({\neg}\)p称为互补对

  子句：有限个文字的析取称为简单析取式，或子句 clause

  短语：有限个文字和合取称为简单合取式，或短语 phrase

合取范式 conjuction normal form

  有限个子句的合取式称为合取范式

析取范式 disjunctive normal form

  有限个短语的析取称为析取范式