【困难】10-正则表达式匹配 Regular Expression Matching

题目

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *

Example1

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

Example2

s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

Example3

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

Example4

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

Example5

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

来源：力扣（LeetCode）
链接：https://leetcode.com/problems/regular-expression-matching

解法

解题思路

判断两个字符串是否全等可以进行简单的逐位判断，但是现在问题的难度集中在*这个符号上，出现*时，*前面的字符的个数是不确定的，比如a*b，可以表示aab也可以表示aaab。如果我们遇到a*就把后面的a全部跳过，那用a*ab检查aaab时，就会发生错误，当遇到.*这样的表达就更棘手了。

由于*的个数是变化的，而且其判定会影响后面字符串的匹配，我们自然联想到动态规划方法。

动态规划的核心是状态和状态转移方程，找到状态和状态转移方程层，问题就迎刃而解了。

状态

首先，题目问什么，什么就是状态，题目问的是字符串为s，正则表达式为p时是否匹配，s和p长度是不定的，而且可以递增，所以，问题可以重述为：长度为m的字符串和长度为n的正则表达式是否匹配，也就是说，可以用bool match[m][n]表示s的前m个字符组成的字符串与p的前n个字符组成的表达式是否匹配

注意：match[m][n]其实表示的是s[0]-s[m-1]与p[0]-p[n-1]匹配

初始状态

我们不需要计算就可以确定的状态是初始状态，也就是p为空的时候（s为空p不为空时也可能匹配）

状态转移方程

如果想要match[m][n]为true，s[m-1] p[n-1]的位置一定是要对应上的，此时，分为三种情况

1. p[n-1]是a-z时，需要s[m-1] == p[n-1] 且 match[m-1][n-1] == true

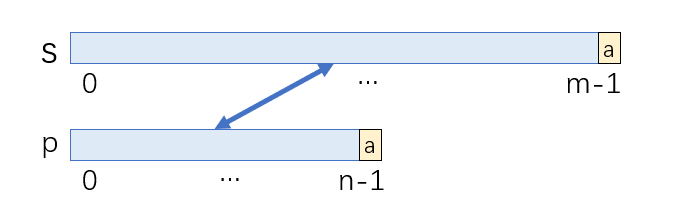
2. p[n-1]是'.'时，s[m-1]可以为任意字符，match[m-1][n-1] == true即可

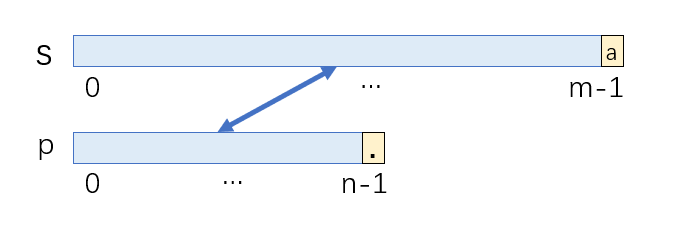
3. 如果p[n-1]是'*'，那么分为两种情况

   • 假设匹配成功时 * 表示个数为0，那么可以当做*和它前面的字符不存在，也就是说只要match[m][n-2]匹配即可

   

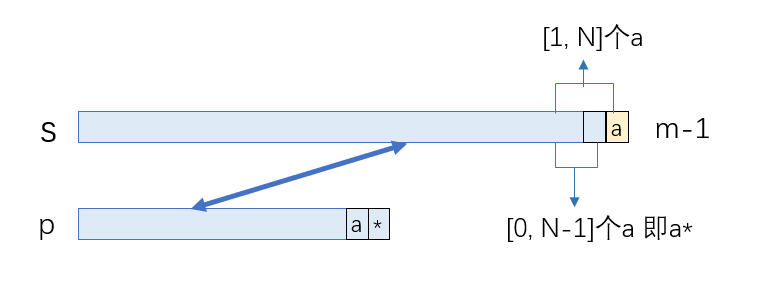
   • 假设匹配成功时*表示个数大于0，那么*前面的字符一定是s[m-1],且match[m-1][n]一定是true,

   

此时，状态转移方程为

match[m][n] = match[m][n-2] or match[m-1][n] and (s[m-1] == p[n-2] or p[n-2] == '.')            (p[n-1] == '*', n>1, m>0)
            = match[m-1][n-1] and (s[m-1] == p[n-1] or p[n-1] == '.')                             (p[n-1] != '*', m>0, n>0)

我们可以发现，对于矩阵match，初始状态是图1中的绿色格子，橙色格子的值会由蓝色格子中的一个决定，通过状态转移方程可以计算出的范围是蓝色斜线的范围，此时，s长度为0的状态还是未知的，而很明显，match[0][n]也会影响后续的判定。

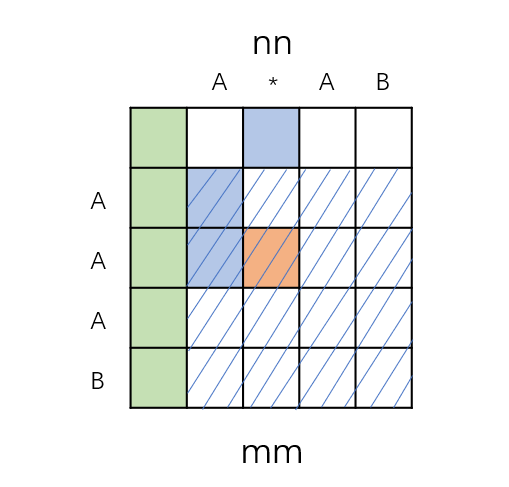
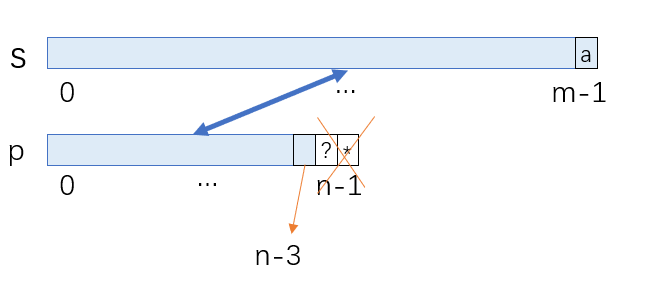
对于s长度为0的情况，我们可以发现，对于match[0][n]，如果p[n-1]不是*，那么一定不匹配，如果p[n-1]是*，这个*代表的个数一定是0，也就是说应为match[0][n-2]

此时，第一行的取值我们也可以计算出来了，理论只要自上向下，自左向右搜索就可以得到最终的结果

最终的状态转移方程为：

match[m][n]  = match[m][n-2] or （m > 0 && match[m-1][n] and (s[m-1] == p[n-2] or p[n-2] == '.')）            (p[n-1] == '*', n>1, m>=0)
             = m > 0 && match[m-1][n-1] and (s[m-1] == p[n-1] or p[n-1] == '.')                             (p[n-1] != '*', m>=0, n>0)

代码

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size(), n = p.size();
        vector<vector<bool>> match(m+1, vector<bool>(n+1));
        match[0][0] = true;
        for(int i = 0; i < m+1; ++i){
            for(int j = 1; j < n+1; ++j){
                if(p[j-1] == '*'){
                    match[i][j] = match[i][j-2] || (i > 0 && match[i-1][j] && (s[i-1] == p[j-2] || p[j-2] == '.'));
                    
                }
                else{
                    match[i][j] = i>0 && match[i-1][j-1] && (s[i-1] == p[j-1] || p[j-1] == '.');
                }
            }
        }
        return match[m][n];
    }
};