BZOJ 2301 Problem b(莫比乌斯反演+分块优化)

Description

对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

Input

第一行一个整数n，接下来n行每行五个整数，分别表示a、b、c、d、k

Output

共n行，每行一个整数表示满足要求的数对(x,y)的个数

Sample Input

2

2 5 1 5 1

1 5 1 5 2

Sample Output

14

3

HINT

100%的数据满足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

题解:这道题其实和之前那道hdu1695很像,反演之后的大函数很好推

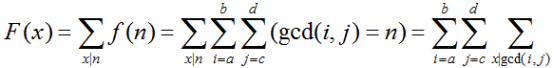
根据容斥原理,答案应该为

其中前一个数为i的上界,后一个数为j的上界

但是我们发现这是O(n^2)的,还是会TLE

这个时候要用一个看着非常dark的方法来优化

这玩意被称之为

分块!

分块!!

分块!!!

其实是假的了

因为我们观察之前的代码:

我们会发现在i极其接近b的时候

在很长的一大段中b/i和d/i都是不变的

所以我们完全可以先处理出莫比乌斯函数的前缀和,然后用前缀和乘上这整个大小不变的块的值即可

代码如下:

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define hi puts("hi");
using namespace std;

int vis[50010],p[50010],mu[50010],sum[50010],cnt,n,a,b,c,d,k;;

void get()
{
    memset(vis,0,sizeof(vis));
    cnt=0;
    mu[1]=1;
    vis[1]=1;
    for(int i=2;i<=50000;i++)
    {
        if(!vis[i])
        {
            p[cnt++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<cnt;j++)
        {
            if(p[j]*i>50000)
            {
                break;
            }
            vis[i*p[j]]=1;
            if(!(i%p[j]))
            {
                mu[i*p[j]]=0;
                break;
            }
            else
            {
                mu[i*p[j]]=-mu[i];
            }
        }
    }
}

long long solve(int x,int y)
{
    long long last=0;
    x/=k;
    y/=k;
    long long ans=0;
    if(x>y)
    {
        swap(x,y);
    }
    for(int i=1;i<=x;i=last+1)
    {
        last=min(x/(x/i),y/(y/i));
        ans+=(long long)(sum[last]-sum[i-1])*(y/i)*(x/i);
    }
    return ans;
}

int main()
{
    get();
    for(int i=1;i<=50000;i++)
    {
        sum[i]=sum[i-1]+mu[i];
    }
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
        long long ans=solve(b,d)+solve(a-1,c-1)-solve(a-1,d)-solve(c-1,b);
        printf("%lld\n",ans);
    }
}