数组中最大的子数组之和

一、程序分析

使用Python语言进行编译，读取一个文件，内容包括数组数和数组元素个，求数组中的最大子数组之和

class MSA:
    #读取文件
    def read_file(self,file_path):
        with open(file_path, "r") as f:
            str = f.read()
        return str      #返回文件内容


    #读取数据预处理
    def pretreatment(self,file_path):
        str=self.read_file(file_path)
        strlist = str.split(":")  # 文件内容按“：”切割为两部分，第一部分为数组长度，第二部分为数组内容
        numlist = strlist[1].split(",")  # 数组内容按“，”切割，获取每个元素
        n = int(strlist[0])
        lst = []
        for i in range(len(numlist)):
            lst.append(int(numlist[i]))
        return lst,n    #返回数组内容列表，数组长度


    #计算最大子数组及下标
    def Calc(self,file_path):
        lst,n=self.pretreatment(file_path)
        max = 0
        for i in range(n):
            for j in range(i, n):
                sum = 0
                for k in range(i, j+1):
                    sum = sum + lst[k]
                    if sum > max:
                        max = sum
                        begin = i
                        end = j - 1
        return max, begin, end      #返回计算结果

if __name__=="__main__":
    file_path="C:/Users/Sun Tianwen/Desktop/data.txt"   #文件路径
    max=0
    begin=0
    end=0
    msa=MSA()
    max,begin,end=msa.Calc(file_path)  #求最大子数组之和及下标

    print("最大子数组的和：",max)
    print("开始下标:",begin)
    print("结束下标:",end)

 

二、单元测试

使用pycharm中的unittest进行测试

单元测试代码

from unittest import TestCase
from max_array import MSA

class TestMSA(TestCase):

    def test_calc_1(self):
        self.MSA=MSA
        self.assertEqual(self.MSA.Calc(self,[-1, 20, -5, 30, -4],5),(45,1,2))

    def test_calc_2(self):
        self.MSA = MSA
        self.assertEqual(self.MSA.Calc(self, [-32, -10, 33, -23, 32, -12, 41, -12, 1, 3, 5, -98, 70, -21, 10, -9, 61], 17), (111, 12, 15))

创建测试文件

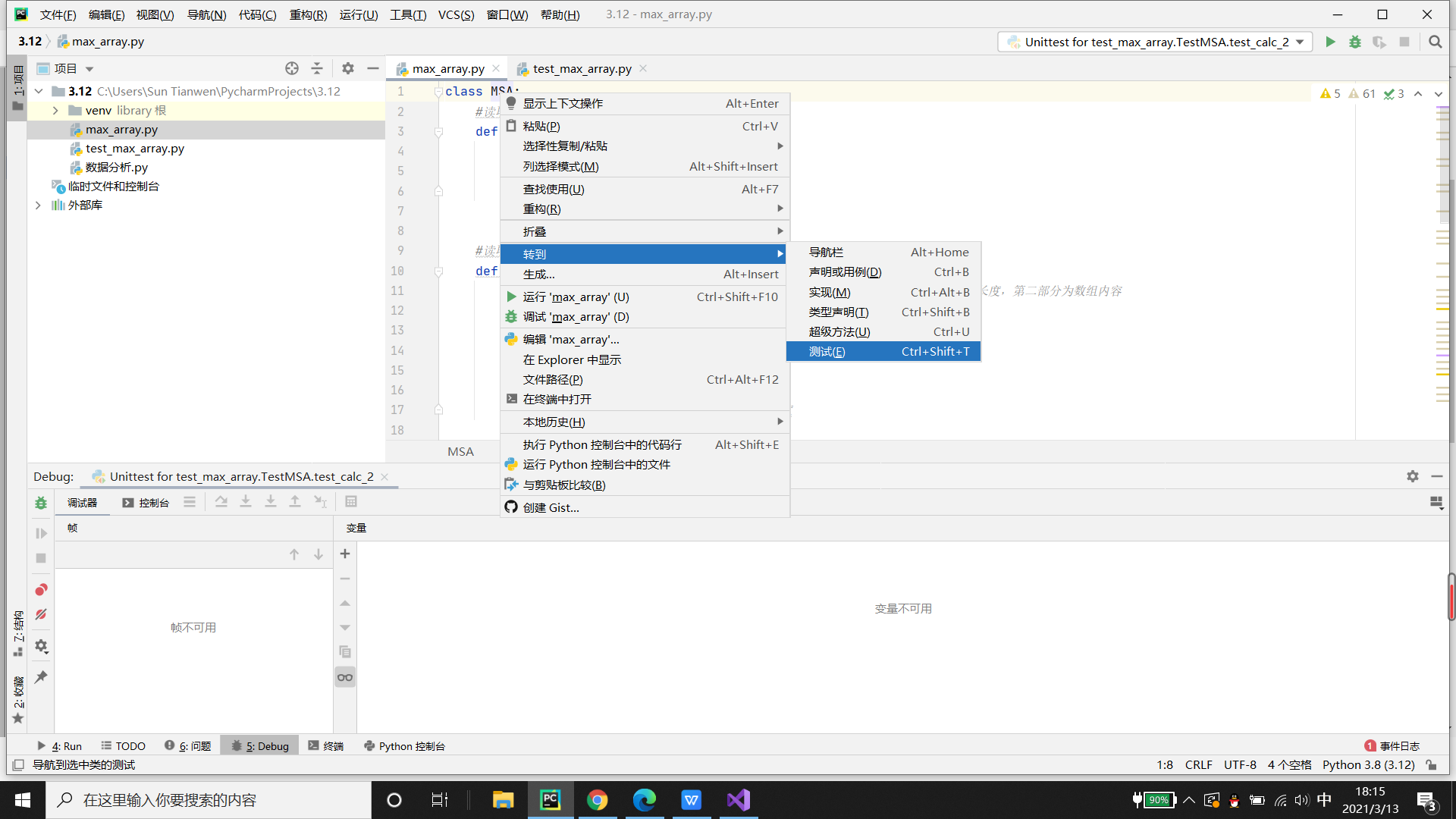
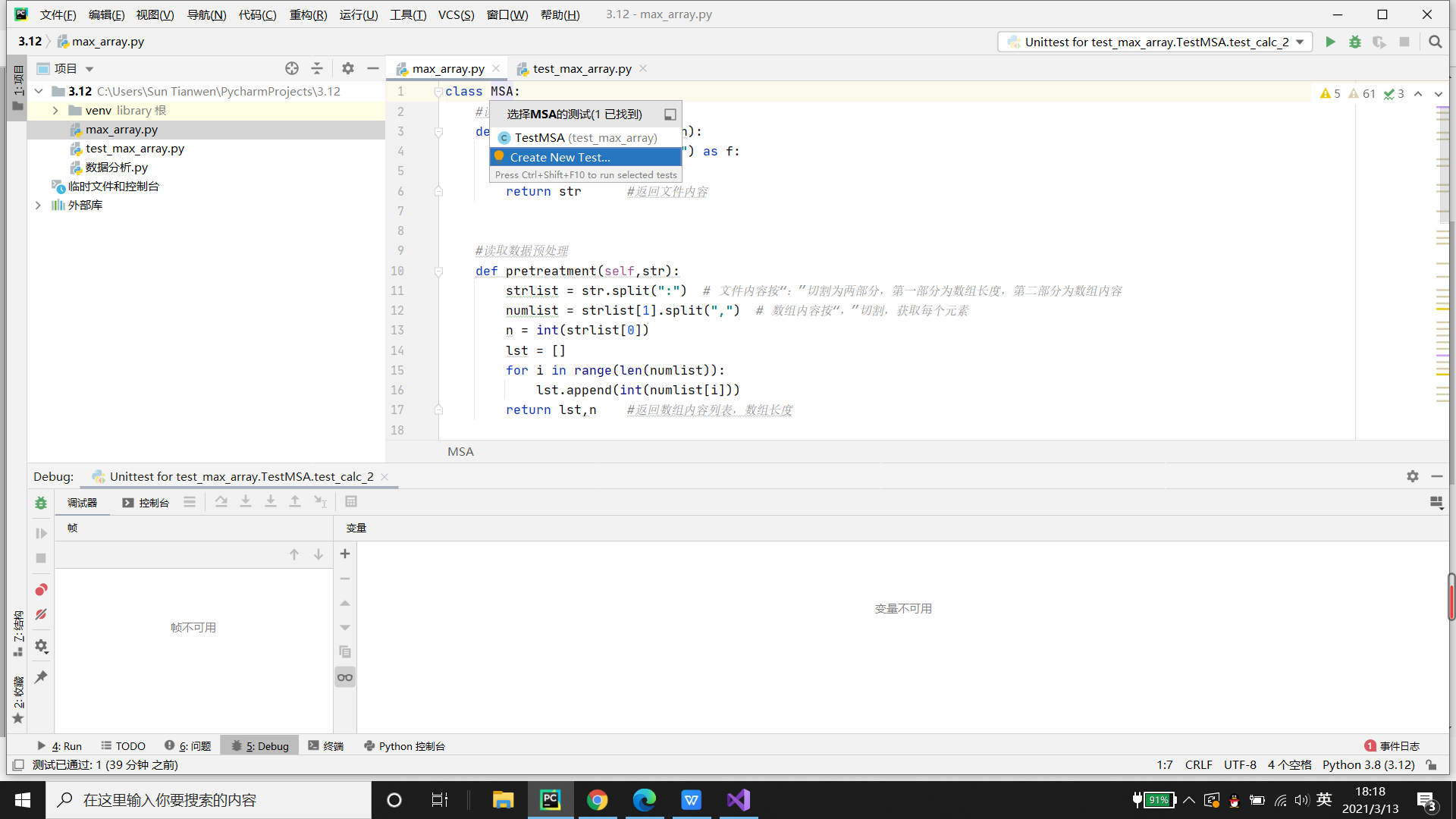
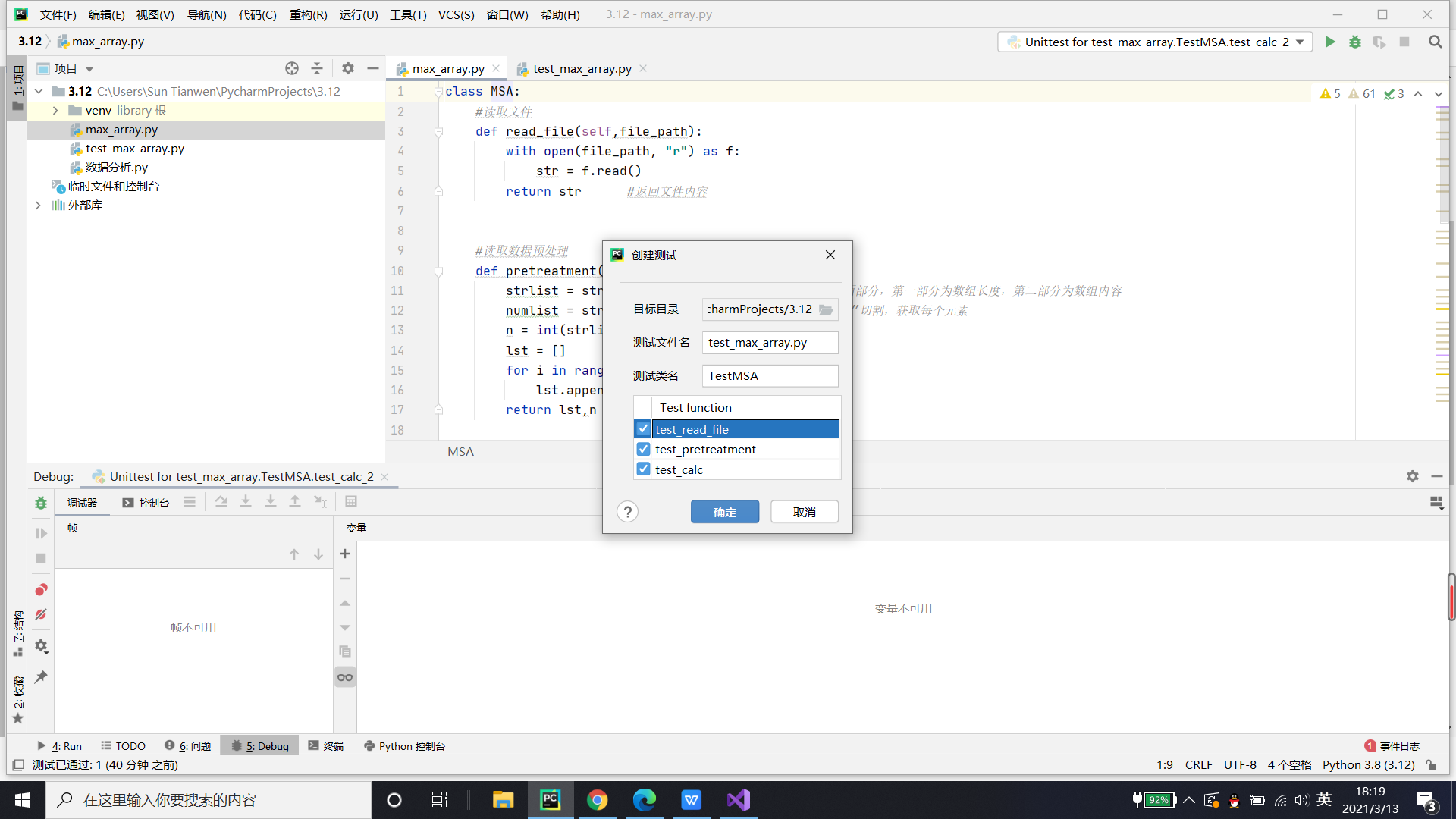
右键创建的类 -->转到-->测试-->Create new test-->输入文件名和勾选要测试的函数-->确定

如图所示

 

 

 

 

 

 

 测试结果

 

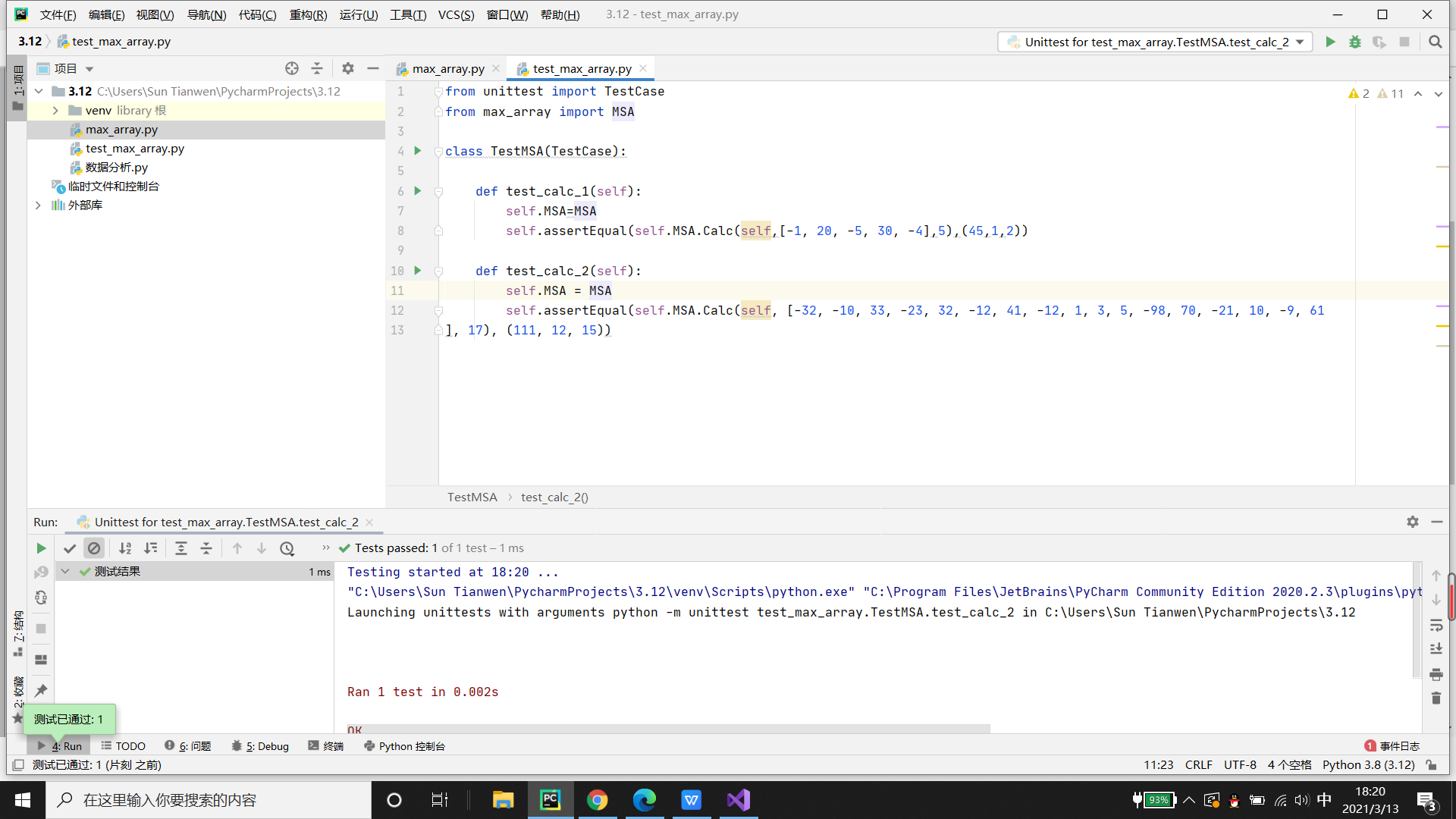
 如上图所示，测试通过

三、性能分析

使用Pycharm的Profile进行性能分析

操作步骤

运行 -->性能分析器 -->配置文件

如图所示

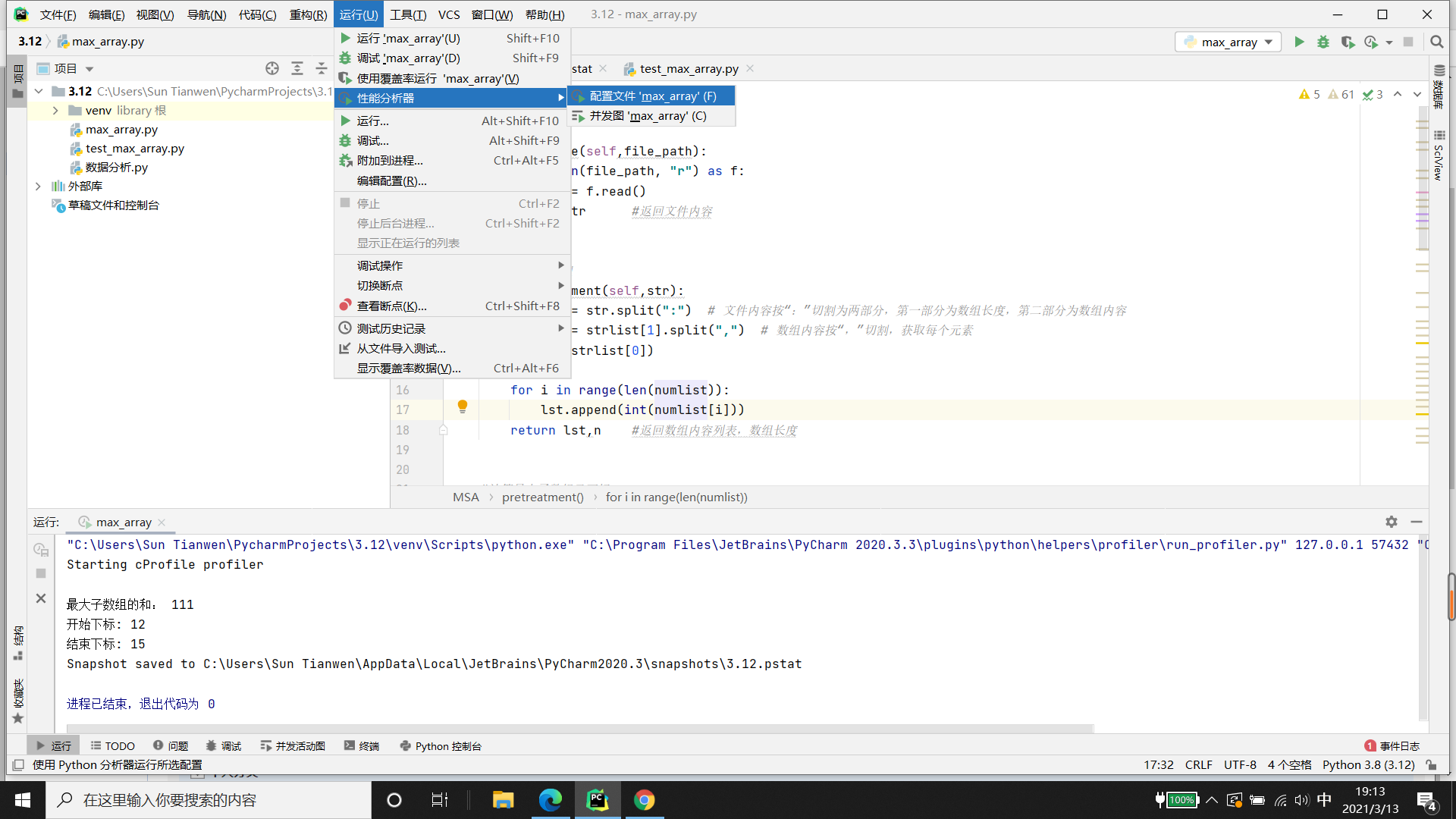
性能统计界面由Statistics和Call Graph两个页面组成，Statistics包括名称、调用计数、时间、自身时间4列组成一个表格，见下图。

(1)表头Name显示被调用的模块或者函数；Call Count显示被调用的次数；Time(ms)显示运行时间和时间百分比，时间单位为毫秒（ms）。

(2)点击表头上的小三角可以升序或降序排列表格。

(3)在Name这一个列中双击某一行可以跳转到对应的代码。

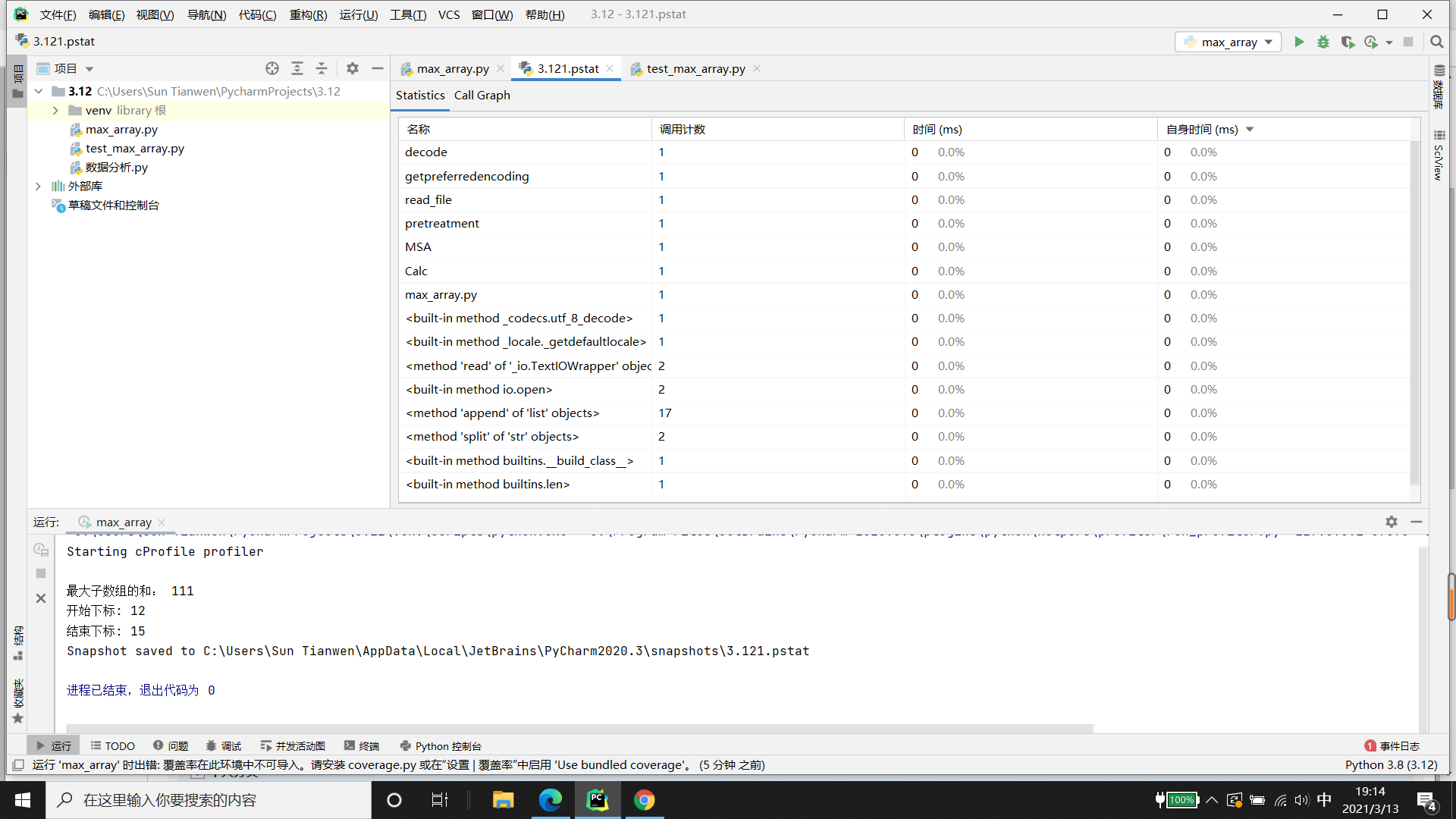
 由于程序规模较小，运行时间被忽略不计，只显示调用计数。

再看Call Graph页面，如图所示，这个界面直观展示了各函数的直接调用关系、运行时间和时间百分比

 

 

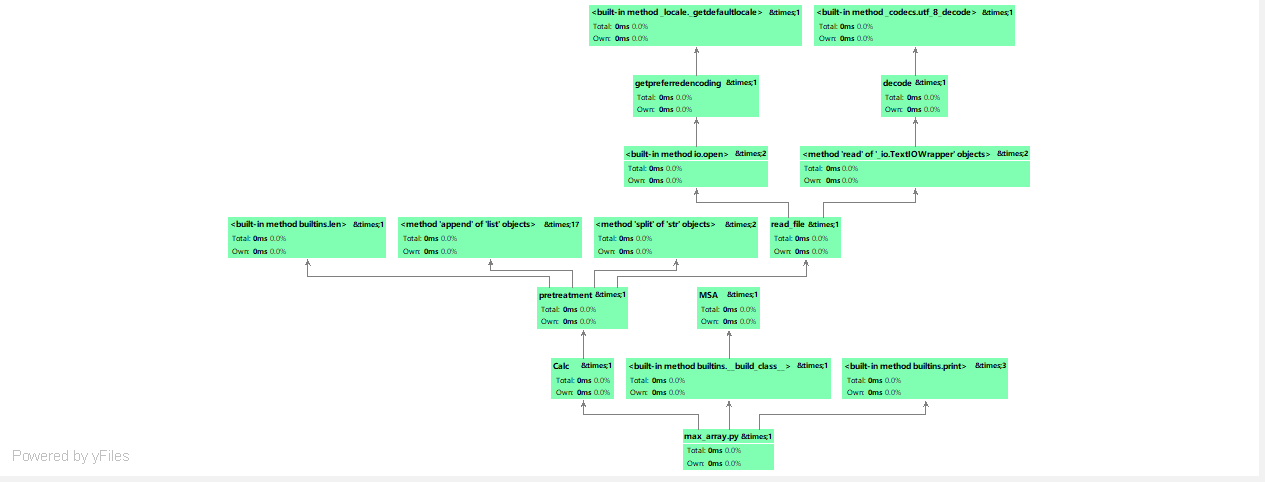
从图中可以看到，Calc函数调用pretreatment函数，pretreament函数再调用read_file函数，直观展示了函数之间的结构。

 改进方法:

1. 改进算法，降低其时间复杂度
2. 使用动态数组存储数据，提高空间的利用效率
3. 尽量避免随意使用静态变量

下面从改进算法方面分析，原代码时间复杂度为O(n^3)，对Calc算法进行改进：

def Calc(self,lst,n):
        max = 0
        sum=0
        for i in range(n):
            sum=0
            for j in range(i,n):
                sum+=lst[j]
                if sum>max:
                    max=sum
                    begin=i
                    end=j
        return max, begin, end      #返回计算结果

改进后时间复杂度为O(n^2),优于原代码