自组合 Self-Assembly UVA1572

题目描述

Automatic Chemical Manufacturing is experimenting with a process called self-assembly. In this process, molecules with natural affinity for each other are mixed together in a solution and allowed to spontaneously assemble themselves into larger structures. But there is one problem: sometimes molecules assemble themselves into a structure of unbounded size, which gums up the machinery.

  You must write a program to decide whether a given collection of molecules can be assembled into a structure of unbounded size. You should make two simplifying assumptions: 1) the problem is restricted to two dimensions, and 2) each molecule in the collection is represented as a square. The four edges of the square represent the surfaces on which the molecule can connect to other compatible molecules.

  In each test case, you will be given a set of molecule descriptions. Each type of molecule is described by four two-character connector labels that indicate how its edges can connect to the edges of other molecules. There are two types of connector labels:

•   An uppercase letter (A, ..., Z) followed by + or -. Two edges are compatible if their labels have the same letter but different signs. For example, A+ is compatible with A- but is not compatible with A+ or B-.
•   Two zero digits 00. An edge with this label is not compatible with any edge (not even with another edge labeled 00).

  Assume there is an unlimited supply of molecules of each type, which may be rotated and reected. As the molecules assemble themselves into larger structures, the edges of two molecules may be adjacent to each other only if they are compatible. It is permitted for an edge, regardless of its connector label, to be connected to nothing (no adjacent molecule on that edge).

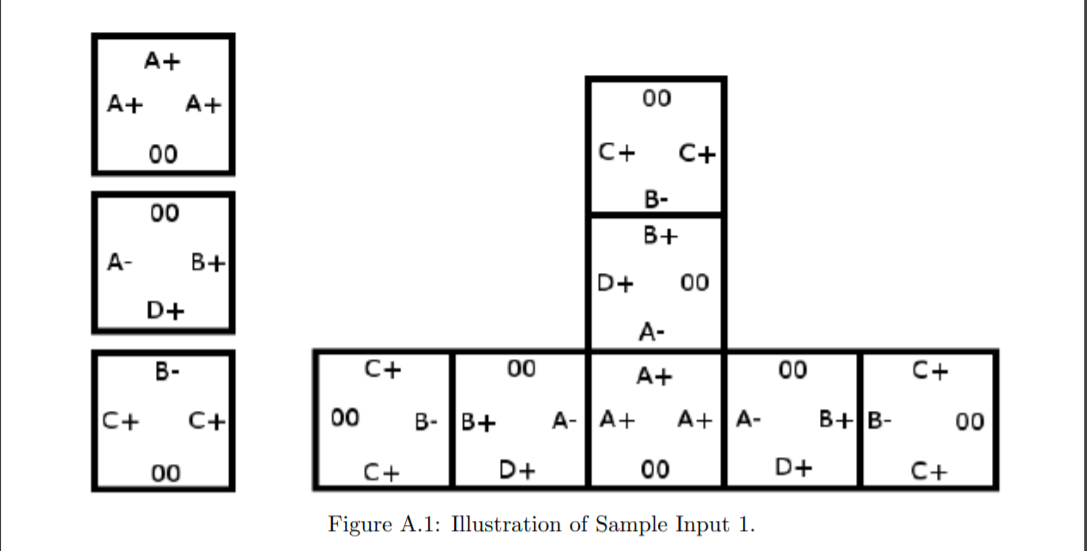
  Figure A.1 shows an example of three molecule types and a structure of bounded size that can be assembled from them (other bounded structures are also possible with this set of molecules).

 输入格式

The input consists of several test cases. A test case consists of two lines. The first contains an integer n (1 ≤ n ≤ 40000) indicating the number of molecule types. The second line contains n eight-character strings, each describing a single type of molecule, separated by single spaces. Each string consists of four two-character connector labels representing the four edges of the molecule in clockwise order.

 输出格式

For each test case, display the word ‘unbounded’ if the set of molecule types can generate a structure of unbounded size. Otherwise, display the word ‘bounded’.

 【输入样例】

3

A+00A+A+ 00B+D+A- B-C+00C+

1

K+K-Q+Q-

【输出样例】

 bounded

unbounded

题目分析

有n（n<=40000）种边上带标号的正方形。每条边要么为一个大写字母后面跟一个加号或者减号，要么为数字00。并且仅当两条边的字母相同且符号相反时，两条边能够拼在一起，00不能和任何包括00的边拼在一起。
假设输入的每种正方形都有无穷多个，而且可以旋转和翻转，任务是判断是否能够成一个无限大的结构，每条边要么悬空，要么和上述可拼接的边相邻。

本题看上去很难下手，但不难发现“可以旋转和翻转”是一个很有意思的条件，值得推敲。“无限大结构”并一定能铺满整个平面，只需要能连出一条无线长的“通路”即可。借助旋转和翻转，可以让这条“通路”总是往右和向下延伸，因此永远不会自交。这样一来，只需要以某个正方形为起点开始“铺路”，一旦可以拼上一块和起点一样的正方形，无线重复下去就能得到一个无限大的结构。

可惜这样的分析仍然不够，因为正方形的数目n很大。进一步分析发现：实际上不需要正方形本身重复，而只需要边上的标号重复即可。这样问题就转化为：把标号看成点（一共只有A+~Z+,A-~Z-这52种，因为00不能作为拼接点），正方形看作边，得到一个有向图。则当且仅当途中存在有向环时有解。只需要做一次拓扑排序即可。

#include <iostream>
#include <cstring>
using namespace std;

//分别代表 A- B- C- D- E- F- G- ………… A+ B+ C+
int G[52][52];
int vis[52];

bool dfs(int i)
{
    vis[i] = -1; //正在访问
    for (int j = 0; j < 52; j++)
    {
        if (G[i][j])
        {
            if (vis[j] == -1)
            {
                //cout << i << "*" << j << endl;
                return false;
            } //环
            if (!vis[j] && !dfs(j))
                return false;
        }
    }
    vis[i] = 1;
    return true;
}

bool topSort()
{
    for (int i = 0; i < 52; i++)
    {
        if (!vis[i])
        {
            if (!dfs(i))
                return false;
        }
    }
    return true;
}

int main()
{
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    // ios::sync_with_stdio(false);
    // cin.tie(0);
    int n;
    while (cin >> n)
    {
        string s;
        string temp[4];
        memset(vis, false, sizeof(vis));
        memset(G, 0, sizeof(G));
        //构造有向边
        for (int i = 0; i < n; i++)
        {
            cin >> s;
            temp[0] = s.substr(0, 2);
            temp[1] = s.substr(2, 2);
            temp[2] = s.substr(4, 2);
            temp[3] = s.substr(6, 2);
            for (int j = 0; j < 4; j++)
            {
                for (int k = 0; k < 4; k++)
                {
                    if (j == k)
                        continue;
                    if (temp[j] == "00" || temp[k] == "00")
                        continue;
                    int index1 = temp[j][0] - 'A' + (temp[j][1] == '-' ? 0 : 26);
                    int index2 = temp[k][0] - 'A' + (temp[k][1] == '+' ? 0 : 26);
                    G[index1][index2] = 1;
                    //cout << index1 << " " << index2 << endl;
                }
            }
        }
        if (!topSort())
        {
            cout << "unbounded" << endl;
        }
        else
        {
            cout << "bounded" << endl;
        }
    }
}