树

树的概念----树的定义

一棵树是由n（n>0）个元素组成的有限集合，其中：

每个元素称为结点(node)；
有一个特定的结点，称为根结点或树根（root）；
除根结点外，其余结点能分成m（m>=0）个互不相交的有限集合T0,T1,T2,……Tm-1。其中的每个子集又都是一棵树，这些集合称为这棵树的子树。

如下图是一棵典型的树：

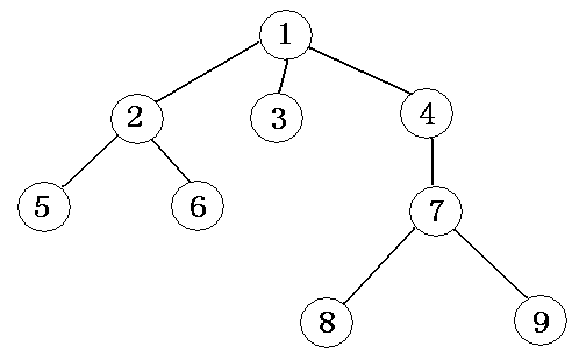
树的基本概念

树是递归定义的；
一棵树中至少有1个结点。这个结点就是根结点，它没有前驱，其余每个结点都有唯一的一个前驱结点。每个结点可以有0或多个后继结点。因此树虽然是非线性结构，但也是有序结构。至于前驱后继结点是哪个，还要看树的遍历方法，我们将在后面讨论；
一个结点的子树个数，称为这个结点的度（degree，结点1的度为3，结点3的度为0）；度为0的结点称为叶结点（树叶leaf，如结点3、5、6、8、9）；度不为0的结点称为分支结点（如结点1、2、4、7）；根以外的分支结点又称为内部结点（结点2、4、7）；树中各结点的度的最大值称为这棵树的度（这棵树的度为3）。
在用图形表示的树型结构中，对两个用线段（称为树枝）连接的相关联的结点，称上端结点为下端结点的父结点，称下端结点为上端结点的子结点。称同一个父结点的多个子结点为兄弟结点。如结点1是结点2、3、4的父结点，结点 2、3、4是结点1的子结点，它们又是兄弟结点，同时结点2又是结点5、6的父结点。称从根结点到某个子结点所经过的所有结点为这个子结点的祖先。如结点1、4、7是结点8的祖先。称以某个结点为根的子树中的任一结点都是该结点的子孙。如结点7、8、9都是结点4的子孙。
定义一棵树的根结点的层次（level）为1，其它结点的层次等于它的父结点层次加1。如结点2、3、4的层次为1，结点5、6、7的层次为2，结点8、9的层次为3。一棵树中所有的结点的层次的最大值称为树的深度（depth）。如这棵树的深度为3。
对于树中任意两个不同的结点，如果从一个结点出发，自上而下沿着树中连着结点的线段能到达另一结点，称它们之间存在着一条路径。可用路径所经过的结点序列表示路径，路径的长度等于路径上的结点个数减1。如上图中，结点1和结点8之间存在着一条路径，并可用（1、4、7、8）表示这条路径，该条路径的长度为3。注意，不同子树上的结点之间不存在路径，从根结点出发，到树中的其余结点一定存在着一条路径。
森林（forest）是m(m>=0)棵互不相交的树的集合。

树的存储结构

方法1：数组，称为“父亲表示法”。

const int m = 10;           //树的结点数
struct node
{
　　 int data, parent;        //数据域，指针域
};
node tree[m];

优缺点：利用了树中除根结点外每个结点都有唯一的父结点这个性质。很容易找到树根，但找孩子时需要遍历整个线性表。

方法2：树型单链表结构，称为“孩子表示法”。每个结点包括一个数据域和一个指针域（指向若干子结点）。称为“孩子表示法”。假设树的度为10，树的结点仅存放字符，则这棵树的数据结构定义如下：

const int m = 10;           //树的度
typedef struct node;
typedef node *tree;
struct node
{
    char data;             //数据域
    tree child[m];          //指针域，指向若干孩子结点
};
tree t;

缺陷：只能从根（父）结点遍历到子结点，不能从某个子结点返回到它的父结点。但程序中确实需要从某个结点返回到它的父结点时，就需要在结点中多定义一个指针变量存放其父结点的信息。这种结构又叫带逆序的树型结构。

方法3：树型双链表结构，称为“父亲孩子表示法”。每个结点包括一个数据域和二个指针域（一个指向若干子结点，一个指向父结点）。假设树的度为10，树的结点仅存放字符，则这棵树的数据结构定义如下：

const int m = 10;           //树的度
typedef struct node;
typedef node *tree;         //声明tree是指向node的指针类型
struct node
{
    char data;             //数据域
    tree child[m];          //指针域，指向若干孩子结点
    tree father;            //指针域，指向父亲结点
};
tree t;

方法4：二叉树型表示法，称为“孩子兄弟表示法”。也是一种双链表结构，但每个结点包括一个数据域和二个指针域（一个指向该结点的第一个孩子结点，一个指向该结点的下一个兄弟结点）。称为“孩子兄弟表示法”。假设树的度为10，树的结点仅存放字符，则这棵树的数据结构定义如下：

typedef struct node;
typedef node *tree;
struct node
{
    char data;            //数据域
　　tree firstchild, next;    //指针域，分别指向第一个孩子结点和下一个兄弟结点
};
tree t;

例1：找树根和孩子

【问题描述】 　　给定一棵树，输出树的根root，孩子最多的结点max以及他的孩子

【输入格式】 　　第一行：n（结点数<=100），m（边数<=200）。　　

　　　　　　　　以下m行；每行两个结点x和y，表示y是x的孩子(x,y<=1000)。

【输出格式】 　　第一行：树根：root。　　

　　　　　　　　第二行：孩子最多的结点max。　　

　　　　　　　　第三行：max的孩子。

【输入样例】 　　

8 7 　　

4 1 　　

4 2 　　

1 3 　　

1 5 　　

2 6 　　

2 7 　　

2 8

【输出样例】 　　

4 　　

2 　　

6 7 8

【参考程序】

#include <iostream>
using namespace std;
int n, m, tree[101] = {0};
int main()
{
    int i, x, y, root, maxroot, sum = 0, j, Max = 0;
    cin >> n >> m;
    for (i = 1; i <= m; i++)
    {
        cin >> x >> y;
        tree[y] = x;
    }
    for (i = 1; i <= n; i++) //找出树根
        if (tree[i] == 0)
        {
            root = i;
            break;
        }
    for (i = 1; i <= n; i++) //找孩子最多的结点
    {
        sum = 0;
        for (j = 1; j <= n; j++)
            if (tree[j] == i)
                sum++;
        if (sum > Max)
        {
            Max = sum;
            maxroot = i;
        }
    }
    cout << root << endl << maxroot << endl;
    for (i = 1; i <= n; i++)
        if (tree[i] == maxroot)
            cout << i << " ";
    return 0;
}

树的遍历

在应用树结构解决问题时，往往要求按照某种次序获得树中全部结点的信息，这种操作叫作树的遍历。遍历的方法有多种，常用的有：　　

先序（根）遍历：先访问根结点，再从左到右按照先序思想遍历各棵子树。如上图先序遍历的结果为：125634789；　　
后序（根）遍历：先从左到右遍历各棵子树，再访问根结点。如上图后序遍历的结果为：562389741；　　
层次遍历：按层次从小到大逐个访问，同一层次按照从左到右的次序。如上图层次遍历的结果为：123456789；　　
叶结点遍历：有时把所有的数据信息都存放在叶结点中，而其余结点都是用来表示数据之间的某种分支或层次关系，这种情况就用这种方法。如上图按照这个思想访问的结果为：56389；

1、2两种方法的定义是递归的，所以在程序实现时往往也是采用递归的思想。既通常所说的“深度优先搜索”。如用先序遍历编写的过程如下：

void tral(tree t, int m)
{
    if (t)
    {
        cout << t->data << endl;
        for (int i = 0; i < m; i++)
            tral(t->child[i], m);
    }
}

3方法应用也较多，实际上是我们讲的“广度优先搜索”。思想如下：若某个结点被访问，则该结点的子结点应记录，等待被访问。顺序访问各层次上结点，直至不再有未访问过的结点。为此，引入一个队列来存储等待访问的子结点，设一个队首和队尾指针分别表示出队、进队的下标。程序框架如下：

const int n = 100;
int head, tail, i;
tree q[n];
tree p;
void work()　　
{
    tail = head = 1;
    q[tail] = t;
    tail++; //队尾为空
    while (head < tail)
    {
        p = q[head];
        head++;
        cout << p->data << ' ';
        for (i = 0; i < m; i++)
            if (p->child[i])
            {
                　　 q[tail] = p->child[i];
                　　 tail++;　　
            }   　　
    }　
}

例2、单词查找树

【问题描述】 在进行文法分析的时候，通常需要检测一个单词是否在我们的单词列表里。为了提高查找和定位的速度，通常都画出与单词列表所对应的单词查找树，其特点如下：

　　　　1．根结点不包含字母，除根结点外每一个结点都仅包含一个大写英文字母；

　　　 2．从根结点到某一结点，路径上经过的字母依次连起来所构成的字母序列，称为该结点对应的单词。单词列表中的每个单词，都是该单词查找树某个结点所对应的单词；

　　　 3．在满足上述条件下，该单词查找树的结点数最少。

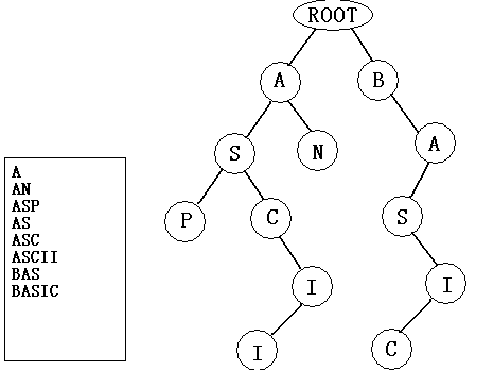
　　　 4．例如图左边的单词列表就对应于右边的单词查找树。注意，对一个确定的单词列表，请统计对应的单词查找树的结点数（包含根结点）。

【问题输入】 输入文件名为word.in，该文件为一个单词列表，每一行仅包含一个单词和一个换行/回车符。每个单词仅由大写的英文字母组成，长度不超过63个字母。文件总长度不超过32K，至少有一行数据。 【问题输出】 输出文件名为word.out，该文件中仅包含一个整数，该整数为单词列表对应的单词查找树的结点数。

【样例输入】 　　

A 　　　

AN 　　　

ASP 　　　

AS 　　　

ASC 　　　

ASCII 　　　

BAS 　　　

BASIC

【样例输出】

13

【算法分析】 首先要对建树的过程有一个了解。对于当前被处理的单词和当前树：在根结点的子结点中找单词的第一位字母，若存在则进而在该结点的子结点中寻找第二位……如此下去直到单词结束，即不需要在该树中添加结点；或单词的第n位不能被找到，即将单词的第n位及其后的字母依次加入单词查找树中去。但，本问题只是问你结点总数，而非建树方案，且有32K文件，所以应该考虑能不能不通过建树就直接算出结点数？为了说明问题的本质，我们给出一个定义：一个单词相对于另一个单词的差：设单词1的长度为L，且与单词2从第N位开始不一致，则说单词1相对于单词2的差为L-N+1，这是描述单词相似程度的量。可见，将一个单词加入单词树的时候，须加入的结点数等于该单词树中已有单词的差的最小值。单词的字典顺序排列后的序列则具有类似的特性，即在一个字典顺序序列中，第m个单词相对于第m-1个单词的差必定是它对于前m-1个单词的差中最小的。于是，得出建树的等效算法：

读入文件；
对单词列表进行字典顺序排序；
依次计算每个单词对前一单词的差，并把差累加起来。注意：第一个单词相对于“空”的差为该单词的长度；
累加和再加上1（根结点），输出结果。就给定的样例，按照这个算法求结点数的过程如下表：

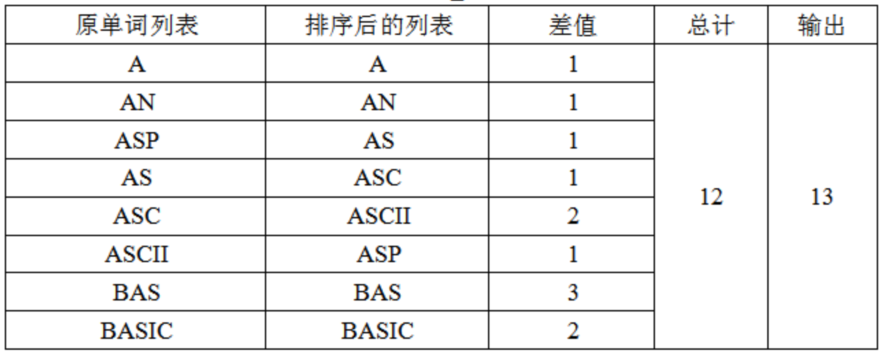
【数据结构】 先确定32K（32*1024=32768字节）的文件最多有多少单词和字母。当然应该尽可能地存放较短的单词。因为单词不重复，所以长度为1的单词（单个字母）最多26个；长度为2的单词最多为26*26=676个；因为每个单词后都要一个换行符（换行符在计算机中占2个字节），所以总共已经占用的空间为：（1+2）*26+（2+2）*676=2782字节；剩余字节（32768-2782=29986字节）分配给长度为3的单词（长度为3的单词最多有 26*26*26=17576个）有29986/（3+2）≈5997。所以单词数量最多为26+676+5997=6699。定义一个数组：string a[32768]；把所有单词连续存放起来，用选择排序或快排对单词进行排序。

#include <iostream>
#include <cstdio>
#include <string>
using namespace std;
int i, j, n, t, k;
string a[8001]; //数组可以到32768
string s;
int main()
{
    freopen("word.in", "r", stdin);
    freopen("word.out", "w", stdout);
    while (cin >> a[++n]); //读入文件中的单词并且存储到数组中
    n--;
    for (i = 1; i < n; i++) //单词从小到大排序，选择排序可改为快排sort(a + 1, a + n + 1)
        for (j = i + 1; j <= n; j++)
            if (a[i] > a[j]) //两个单词进行交换
            {
                s = a[i];
                a[i] = a[j];
                a[j] = s;
            }
    t = a[1].length();       //先累加第1个单词的长度
    for (i = 2; i <= n; i++) //依次计算每个单词对前一单词的差
    {
        j = 0;
        while (a[i][j] == a[i - 1][j] && j < a[i - 1].length())
            j++;                //求两个单词相同部分的长度
        t += a[i].length() - j; //累加两个单词的差length(a[i])-j
    }
    cout << t + 1 << endl;
    return 0;
}

例3、四分树（Quadtree, UVa 297）

【问题描述】

【问题输入】

【问题输出】