前缀和与差分

前缀和与差分

前缀和

对于一个给定得到 \(n\) 个数的序列 \(a\) ，它得前缀和序列 \(s\) ：\(s[i]=\sum_{j=1}^ia[j]\) ，通过递推求解 \(s[0]=0,s[i]=s[i-1]+a[i](1\le i \le n)\) 。

前缀和可以在 \(O(1)\) 的时间求得区间和：\(\sum_{i=l}^ra[i]=s[r]-s[l-1]\) 。

二维前缀和

在二维数组 \(a\) 中，可以按照同样的方式求解二维前缀和。二维前缀和 \(s[i][j]\) 表示左上角为 \(a[1][1]\)，右下角为 \(a[i][j]\) 的矩阵和。

\(s[i][j]=\sum_{x=1}^i \sum_{y=1}^j a[x][y]\)

二维前缀和通过递推求解：\(s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]\) 。

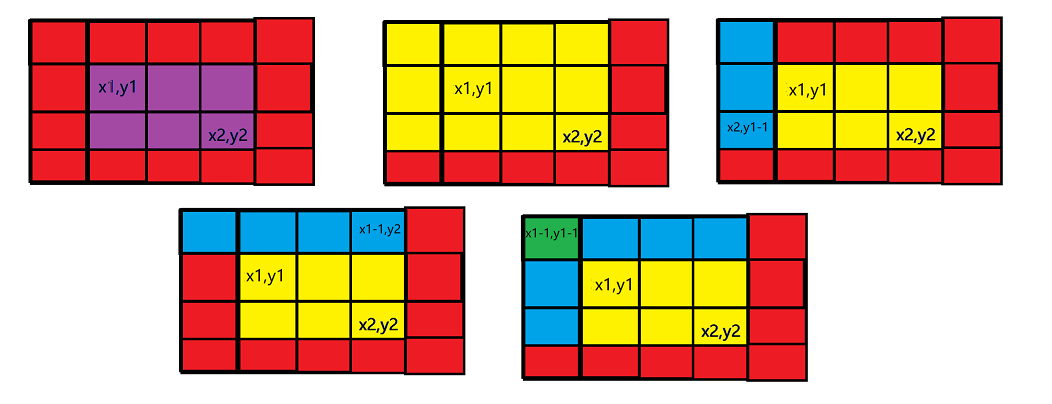
对于左下角为 \(a[x_1][y_1]\)，右上角为 \(a[x_2][y_2]\) 的矩形权值和：

\(SUM\{a[x_1][y_1]\sim a[x_2][y_2]\}=s[x_2][y_2]−s[x_2][y_1−1]−s[x_1−1][y_2]+s[x_1−1][y_1−1]\)

上面两个式子的思想其实就是容斥原理。

树上前缀和

设 \(s_i\) 表示节点 \(i\) 到根节点的权值综合。

若是点权，\(x,y\) 之间的路径权值和为：\(s_x+s_y-s_{lca}-s_{fa[lca]}\) 。

若是边权，\(x,y\) 之间的路径权值和为：\(s_x+s_y-2s_{lca}\) 。

只要有可加可减性的信息都按照前缀和的方式，还可以求出前缀积、前缀异或和等等 。

差分

对于一个给定得到 \(n\) 个数的序列 \(a\) ，它的差分序列 \(b\) 定义为：

\(b[1]=1,b[i]=a[i]-a[i-1](2\le i \le n)\)

对于区间 \([l,r]\) 所有元素增加 \(d\) ，可以更新差分序列来进行区间加：\(b[l]=b[l]+d,b[r+1]=b[r+1]-d\) ，将 \(1\) 次区间操作转化为 \(2\) 次单点操作。

前缀和与差分是一对互逆运算，差分序列 \(b\) 的前缀和序列就是 \(a\) ，前缀和序列 \(s\) 的差分序列也是序列 \(a\) 。

二维差分

给定矩阵 \(a\) ，定义二维差分序列 \(b\) ，\(b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]\) 。

对于矩阵中对左上角 \(a[x_1][y_1]\) ，右下角 \(a[x_2][y_2]\) 的矩阵整体增加 \(d\) ，对于二维差分序列 \(b\) ，只有 \(4\) 个元素会改变：

b[x1][y1]+=d;
b[x2+1][y1]-=d;
b[x1][y2+1]-=d;
b[x2+1][y2+1]+=d;

差分序列 \(b\) 的二维前缀和(左上角 \(b[1][1]\)，右下角 \(b[i][j]\) 矩形) 就是 \(a[i][j]\) 。

练习：[洛谷 P3397] 地毯

树上差分

树有这样两个性质：
（1）树上任意两个点的路径唯一。
（2）任何子节点的父亲节点唯一(可以认为根节点是没有父亲的，或者用0代替)。
树上差分可以处理路径修改。

点差分

给定一棵 \(n\) 个点的树，进行 \(m\) 次操作，每次操作从节点 \(x\) 到 \(y\) ，对路径上经过所有点的点权加 \(d\) ，输出最后每个点的权值。

朴素做法， \(x,y\) 同时往 \(lca(x,y)\) 走，对经过的点权值 \(+d\) 。时间复杂度为 \(O(nm)\) 。

使用点差分。

定义 \(nd[u]\) 表示经过 \(u\) 和 \(u\) 的祖先节点（\(u\) 到根节点）的次数。

设 \(f[u]\) 为经过 \(u\) 的次数，\(f[u]\) 就是 \(u\) 为根的子树的所有节点的 \(nd\) 和。

若 \(v\) 为 \(u\) 的子节点，\(f[u]=nd[u]+\sum f[v]\) ，递归求解即可。

设 \(fa[x]\) 表示 \(x\) 的父亲节点，\(lca(x,y)\) 表示 \(x,y\) 的最近公共祖先。那么，修改 \(x\) 到 \(y\) 的路径，全部增加 \(d\) 。只需要修改 \(4\) 个节点：

nd[x]+=d;
nd[y]+=d;
nd[lca(x,y)]-=d;
nd[fa[lca(x,y)]]-=d;

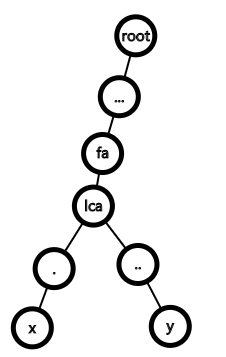
nd[x]++ ，\(x\) 到根 \(root\) 路径权值全部 \(+d\) ；nd[y]++ ，\(y\) 到根 \(root\) 路径全部 \(+d\) 。\(lca\) 到根 \(root\) 路径增加了两次，且 \(lca\) 的权值需要增加，而 \(fa\) 到 \(root\) 的路径不需要增加，因此需要 nd[lca]-=d;nd[fa]-=d 。路径修改的时间复杂度为 \(O(\log n)\) 。

因此，预处理 \(lca\) 的时间复杂度为 \(O(n \log n)\) ，整个时间复杂度为 \(O(n \log n+ m \log n)\) 。

边差分

给定一棵 \(n\) 个点的树，进行 \(m\) 次操作，每次操作从节点 \(x\) 到 \(y\) ，对路径上经过的所有边的边权加 \(d\) ，输出最后每条边的边权。

定义 \(ed[u]\) 表示 \(u\) 到祖先所有边经过的次数。

修改 \(x\) 到 \(y\) 的路径，只需要修改 \(3\) 个节点：

ed[u]+=d;
ed[v]+=d;
ed[lca]-=2*d;

\(lca\) 到 \(root\) 的路径边权不需要增加，但增加了两次，需要 \(-2*d\) 。

设 \(f[u]\) 为经过 \(u\) 的到父节点边的次数，\(f[u]\) 就是 \(u\) 为根的子树的所有节点的 \(nd\) 和。

若 \(v\) 为 \(u\) 的子节点，\(f[u]=\sum f[v]\) ，递归求解即可。

练习：

「JLOI2014」松鼠的新家

「POJ3417」暗的连锁