计算机如何存储浮点数

前言

计算机使用二进制来存储所有数据，对于整数，直接转成二进制就可以了，如int类型的15，二进制表示为

00000000 00000000 00000000 00001111

对于浮点数，如何转换成二进制呢，答案是使用IEEE 754标准。

原理

IEEE 754规定，对于32位的浮点数，最高1位是符号位S，接着的8位是指数E，剩下的23位为有效数字M。

对于64位的浮点数，最高1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

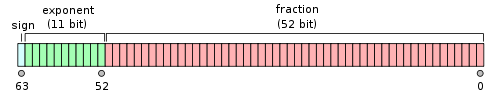
以32位浮点数为例，计算公式为

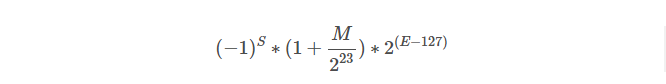
• S: 符号位，0表示正数，1表示负数。
• E: 指数
• M: 尾数

以32位浮点数3.25为例，转为二进制为11.01，规范表示为1.101 * 2¹，所以
S=0，
E=1+127=128，二进制为10000000
M=101(省略掉左侧的1之后)，不足23位右侧补0，超过23位截取前23位，最终结果为

0 10000000 10100000000000000000000

十进制表示为1078984704。

Java代码

public class Client {

  public static void main(String[] args) {
    System.out.println(Float.floatToIntBits(3.25f));//1078984704
    System.out.println(Float.intBitsToFloat(1078984704));//3.25
    System.out.println(Double.doubleToLongBits(3.25f));//4614500768194494464
    System.out.println(Double.longBitsToDouble(4614500768194494464L));//3.25
  }

}

Java提供了符合IEEE 754标准的表示浮点数的方法，将整型数和浮点数进行转换。

注意

十进制转二进制，如3.25，整数部分采用除2取余，逆序排列法，小数部分采用乘2取整法，具体可以查看10进制转2进制。
小数部分在转换时，有可能剩余部分一直不为0，一直无限循环，我们只能根据精度取有限的位数，这也是浮点数会丢失精度的原因。如

System.out.println(0.3 - 0.2);//0.09999999999999998

结果不是预期的0.1。处理浮点数相关，推荐使用BigDecimal。

参考

IEEE 754浮点数标准详解
10进制转2进制
浮点数的二进制表示
计算机如何存储浮点数