P5074 Eat the Trees

简要题意

给出 \(n\times m\) 的方格，有些格子不能铺线，其它格子必须铺，可以形成多个闭合回路。问有多少种铺法？

前置知识

dp，状压，轮廓线

思路

1. 因为观察到数据范围 \(1\le n,m\le 12\) 所以思考一些搜索，状压等时间复杂度比较高的做法。搜索显然不好维护。考虑状压。

2. 状压维护什么东西？（因为这是一道模板题所以直接说了）我们要维护轮廓线上的插头状态。出现了两个词，轮廓线表示当前我已经处理完的各自的边缘(原本的边缘不要)组成的线。插头状态是指有没有线铺到了这个位置（转移时需要考虑这条这么延伸）。

3. 然后写出 dp 。设 \(dp_{i,j,s}\) 表示处理到 \(i\) 行 \(j\) 列（i,j还没处理）轮廓线的状态是 \(s\) 的方案数。答案就是 \(dp_{n,m,0}\) 就是结尾没有任何插头的方案数。然后考虑转移，如果我们知道上一个格子怎么推下一个，显然就考虑 \(（i,j）\) 这个位置填什么（不能随便填要根据 \(s\) 合法填入）。比方说这个格子左边有上边有，那么在这就可以闭合了，转移到左边无上边无的状态。看一张图理解一下(黄色是i,j的轮廓线，橙色是i,j+1的轮廓线，红色是左边和上边的插头，蓝色是新的插头)。0

   

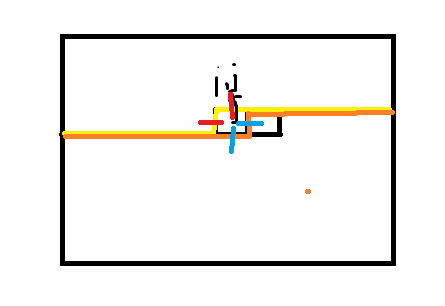
   4. 请注意，当下一个位置在下一行的时候特殊处理一下。

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=13,M=9e3+10;
int n,m,a[N][N],dp[N][N][M];
void solve()
{
	cin>>n>>m;
	int len=(1<<(m+1));
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>a[i][j]; 
	dp[0][m][0]=1;//初始化
	for(int i=1;i<=n;i++) //枚举行数 
	{
		for(int s=0;s<len;s++)dp[i][0][s<<1]=dp[i-1][m][s];//从上一行转移过来（从左往右对应二进制从高到低）
		for(int j=1;j<=m;j++)
		{
			for(int s=0;s<len;s++)//等于 
			{
				int p=(1<<j),q=(1<<(j-1));//方便进行位运算 
				int x=s&p,y=s&q;//取出插头
				if(!a[i][j])//是障碍
				{
					if(!x&&!y)//只能没有插头 
						dp[i][j][s]+=dp[i][j-1][s];//从上一个位置也没有插头转移 
				} 
				else if(x&&y&&a[i+1][j]&&a[i][j+1])//可以新开两个插头
				{
					dp[i][j][s]+=dp[i][j-1][s^p^q];//从上一个位置也没有插头转移
				} 
				else if(!x&&y&&a[i+1][j])//可以向下插
				{
					dp[i][j][s]+=dp[i][j-1][s^p^q]+dp[i][j-1][s]; 
				} 
				else if(x&&!y&&a[i][j+1])//可以向右插
				{
					dp[i][j][s]+=dp[i][j-1][s^p^q]+dp[i][j-1][s]; 
				} 
				else if(!x&&!y) dp[i][j][s]+=dp[i][j-1][s^p^q];//合并 
			}
		} 
	}
	cout<<dp[n][m][0]<<'\n';
	for(int i=0;i<=n;i++)
		for(int j=0;j<=m;j++)
			for(int s=0;s<=len;s++)
				dp[i][j][s]=0;//清零
	return; 
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	int t;cin>>t;
	while(t--)solve();
	return 0;
}