【AT4378】Modulo Matrix

题目

题目链接：https://www.luogu.com.cn/problem/AT4378

构造一个 \(N*N\) 的矩阵. 要求:

• 所有元素互不相同。
• 满足 \(a_{i,j}\leq 10^{15}\)。
• 对于任意两个相邻的数字 \(x,y\)，满足\(\max(x,y)\bmod \min(x,y)\) 都相等，且均为正整数。

可以证明方案一定存在。

思路

由于只有相邻格子有限制，所以可以先将格子黑白染色

考虑如下图构造：

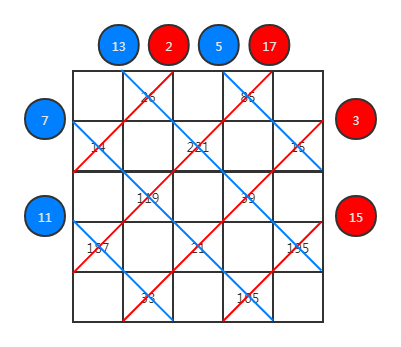
所有白色格子所在的斜线分成红蓝两种，每条斜线有一个唯一的质数，每个白色格子的数字即为两条斜线上质数的积。

然后令每一个黑色格子上的数字为相邻白色格子的数字的 \(\operatorname{lcm}+1\)。显然这样满足任意两个相邻格子大数取模小数均为 1，且数字不会重复。

从 OEIS 的表中可以看到第 \(1000\) 个质数是不超过 \(8000\) 的，所以白色格子的数字最大为 \(8000^2\)，黑色格子的最大数字为 \(8000^4\)。

但是 \(8000^4=4.096\times 10^{15}\)，所以为了避免超过 \(10^{15}\)，考虑将两条相邻的红线和蓝线的质数相差尽量大，或者说随机一下（看脸，我的没过233）。

时间复杂度 \(O(n^2)\)。

代码中给出检验答案是否合格的 伪\(\operatorname{SPJ}\)。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;

const int N=510;
int n,prm[N*2];
ll a[N][N];

struct node
{
	int dat,prm;
}b[N*2];

bool cmp(node x,node y)
{
	return x.dat<y.dat;
}

void findprm(int k)
{
	for (int i=2,m=0;m<k;i++)
	{
		bool flag=1;
		for (int j=2;j*j<=i;j++)
			if (i%j==0) flag=0;
		if (flag) prm[++m]=i;
	}
}

ll query(int x,int y,int opt)
{
	if (opt==1) return b[(x+y)/2].prm;
		else return b[(n+x-y+1)/2+n].prm;
}

int main()
{
	scanf("%d",&n);
	if (n==2) return !printf("4 7\n23 10"); // 如果不特判 n=2，那么左上角和右下角的数字一样
	findprm(2*n);
	for (int i=1;i<=2*n;i++)
	{
		if (i<=n) b[i].dat=i*2-1;
			else b[i].dat=(2*n-i)*2;
		b[i].prm=prm[i];
	}
	sort(b+1,b+1+2*n,cmp);
	for (int i=1;i<=n;i++,putchar(10))
		for (int j=1;j<=n;j++)
			if ((i+j)&1)
				printf("%lld ",query(i,j,1)*query(i,j,2));
			else  //处理黑点，注意特判角上的点
			{
				if (1<i && i<n)
					printf("%lld ",query(i-1,j,1)*query(i-1,j,2)*query(i+1,j,1)*query(i+1,j,2)+1);
				else if (1<j && j<n)
					printf("%lld ",query(i,j-1,1)*query(i,j-1,2)*query(i,j+1,1)*query(i,j+1,2)+1);
				else if (i==1 && j==1)
					printf("%lld ",query(i,j+1,1)*query(i,j+1,2)*query(i+1,j,2)+1);
				else if (i==1 && j==n)
					printf("%lld ",query(i,j-1,1)*query(i,j-1,2)*query(i+1,j,1)+1);
				else if (i==n && j==1)
					printf("%lld ",query(i,j+1,1)*query(i,j+1,2)*query(i-1,j,1)+1);
				else if (i==n && j==n)
					printf("%lld ",query(i,j-1,1)*query(i,j-1,2)*query(i-1,j,2)+1);
				else puts("WYC AK IOI!!!!!");
			}
	return 0;
}

伪\(\operatorname{SPJ}\):

#include <cstdio>
#include <algorithm>
using namespace std;

const int dx[]={0,0,0,-1,1},dy[]={0,-1,1,0,0};
long long maxn,a[600][600];
int n;

int main()
{
	scanf("%d",&n);
	freopen("ans.txt","r",stdin);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			scanf("%lld",&a[i][j]);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			for (int k=1;k<=4;k++)
			{
				int x=i+dx[k],y=j+dy[k];
				if (x<1 || y<1 || x>n || y>n) continue;
				long long p=max(a[i][j],a[x][y]),q=min(a[i][j],a[x][y]);
				if (p>maxn) maxn=p;
				if (p%q!=1) return !printf("WA");
			}
	if (maxn>1000000000000000LL) printf("Your answer is : %lld",maxn);
		else printf("AC");
	return 0;
}