AtCoder Beginner Contest 213

AtCoder Beginner Contest 213 - AtCoder

C - Reorder Cards

本题考查离散化，我们将所有出现过的\(x\)，\(y\)分别存下来并排序去重，给它们重新编号并输出即可。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 5;
pair<int, int> V[MAXN];
int main(int argc, char *argv[]) {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int h, w, n;
    cin >> h >> w >> n;
    vector<int> X, Y;
    for (int i = 1; i <= n; ++i) {
        int x, y;
        cin >> x >> y;
        V[i] = {x, y};
        X.push_back(x);
        Y.push_back(y);
    }
    // vector排序并去重
    auto discrete = [](vector<int>& V) -> void {
        sort(V.begin(), V.end());
        V.erase(unique(V.begin(), V.end()), V.end());
    };
    discrete(X);
    discrete(Y);
    // 重新编号
    auto getIdx = [](vector<int>& V, int x) -> int {
        return lower_bound(V.begin(), V.end(), x) - V.begin() + 1;
    };
    for (int i = 1; i <= n; ++i) {
        auto [x, y] = V[i];
        cout << getIdx(X, x) << ' ' << getIdx(Y, y) << '\n';
    }
    system("pause");
    return 0;
}

D - Takahashi Tour

按照题意模拟即可，注意边存下来后要先遍历小的，可以利用\(vector\)存边并排序，题目给的第二个条件其实就是\(dfs\)回溯的过程。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 5;
bool vis[MAXN];
vector<int> e[MAXN], path;
void dfs(int u) {
    for (int v: e[u]) {
        if (vis[v]) continue;
        vis[v] = true;
        path.push_back(v); // 先到v
        dfs(v);
        path.push_back(u); // 回到u
    }
}
int main(int argc, char *argv[]) {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    for (int i = 1; i < n; ++i) {
        int u, v;
        cin >> u >> v;
        e[u].push_back(v);
        e[v].push_back(u);
    }
    for (int i = 1; i <= n; ++i) {
        sort(e[i].begin(), e[i].end());
    }
    vis[1] = true;
    path.push_back(1);
    dfs(1);
    for (auto it: path) {
        cout << it << ' ';
    }
    system("pause");
    return 0;
}

E - Stronger Takahashi

本题初看没啥思路，但是我们可以重新理解下题目所说的破坏一个\(2×2\)的矩阵，我们可以把这个操作理解为花费\(1\)的费用使得接下来周围的几个点全部可达。

那么本题就可以用最短路解决了，考虑如下建边的方式：

\(\bullet\) 对于每个点，我们从它向四周连一条费用为\(0\)的边，如果是墙壁则不连边。

\(\bullet\) 对于每个点，我们从它向四周\(5×5\)的矩阵连一条费用为\(1\)的边，注意矩阵周围四个角不连。

然后跑最短路即可。

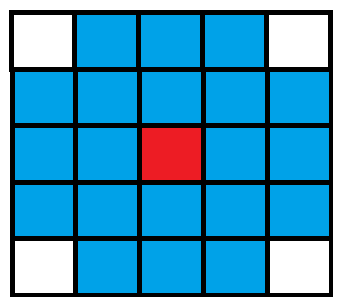
为什么是\(5×5\)呢，可以看下图：

假设当前我们所在位置在下图红色点。

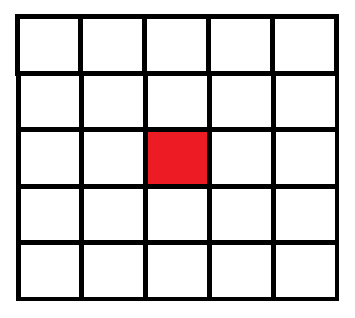
通过操作二，我们可以到达如下几个矩阵：

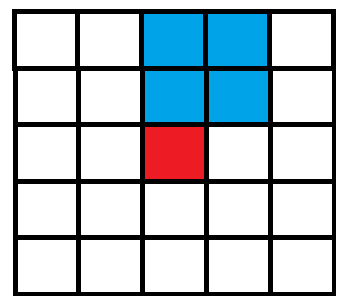
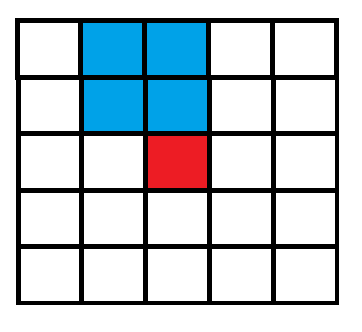
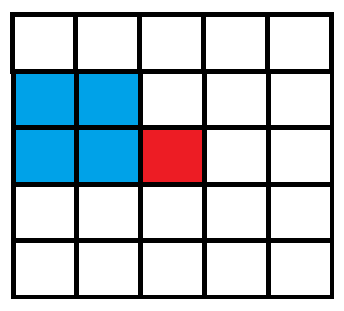
\(\cdots\)

那么最终它全部可达的点就如下图所示：

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 500 * 500 + 50;
struct edge {
    int to, next, val;
} e[MAXN << 5];
int head[MAXN], idx;
void addedge(int u, int v, int w) {
    e[++idx] = edge{v, head[u], w};
    head[u] = idx;
}
struct GraphNode {
    int u, dist;
    bool operator <(const GraphNode& oth) const {
        return oth.dist < dist;
    }
};
bool vis[MAXN];
int dist[MAXN];
void dijkstra(int s) {
    priority_queue<GraphNode> Q;
    memset(vis, false, sizeof(vis));
    memset(dist, 0x3f, sizeof(dist));
    dist[s] = 0, Q.push({s, dist[s]});
    while (!Q.empty()) {
        int u = Q.top().u; Q.pop();
        if (vis[u]) continue;
        vis[u] = true;
        for (int i = head[u]; i; i = e[i].next) {
            int v = e[i].to, w = e[i].val;
            if (dist[u] + w < dist[v]) {
                dist[v] = dist[u] + w;
                Q.push({v, dist[v]});
            }
        }
    }
}
char g[505][505];
int n, m, ID[505][505];
int main(int argc, char *argv[]) {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    int cnt = 0;
    // 对每个点编号方便建图
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            cin >> g[i][j];
            ID[i][j] = ++cnt;
        }
    }
    // 方向数组
    int d[4][2] = {
        {0, 1}, {0, -1}, {1, 0}, {-1, 0}
    };
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            for (int k = 0; k < 4; ++k) {
                int nx = i + d[k][0], ny = j + d[k][1];
                if (1 <= nx && nx <= n && 1 <= ny && ny <= m) {
                    if (g[nx][ny] == '.') {
                        addedge(ID[i][j], ID[nx][ny], 0);
                    }
                }
            }
            // 这里矩阵建边直接for循环比较方便
            for (int x = -2; x <= 2; ++x) {
                for (int y = -2; y <= 2; ++y) {
                    if (abs(x) == 2 && abs(y) == 2) continue; // 如果是角落则不建边
                    int nx = i + x, ny = j + y;
                    if (1 <= nx && nx <= n && 1 <= ny && ny <= m) {
                        addedge(ID[i][j], ID[nx][ny], 1);
                    }
                }
            }
        }
    }
    dijkstra(1);
    cout << dist[n * m] << '\n';
    system("pause");
    return 0;
}