算法实践6 选取第k小元素

问题：

在序列中选取第k小的数字。

解析

我们先选取一个数字\(x\)，当序列中小于\(x\)的数字的数量为\(k - 1\)时，\(x\)就是我们要找的数字；数量大于等于\(k\)时，第\(k\)小的数字小于等于\(x\)；数量小于\(k\)时，第\(k\)小的数字大于等于\(x\)。我们将序列分成若干个五元组，将这个结论推广到二维序列中。

再按照上面的结论，选择S1或者S2继续进行同样的操作。当序列数量小于一定值时，直接取出第k小的数字。

设计

int gao(int a[], int n, int k) {
    规模较小的问题直接输出答案
    分组找中位数
    在中位数中找中位数
	for(遍历每个组的中位数) 
        if 中位数与m*相同，可以直接分
        else if 中位数小于m*，小的数字直接分到s1，遍历大的
        else 中位数大于m*，大的直接分到s2，遍历小的
    if (s1.size() == k - 1)  m*就是第k小的数
    if (s1.size() >= k) 第k小的数在小的序列里
    else 第k小的数在大的序列里
}

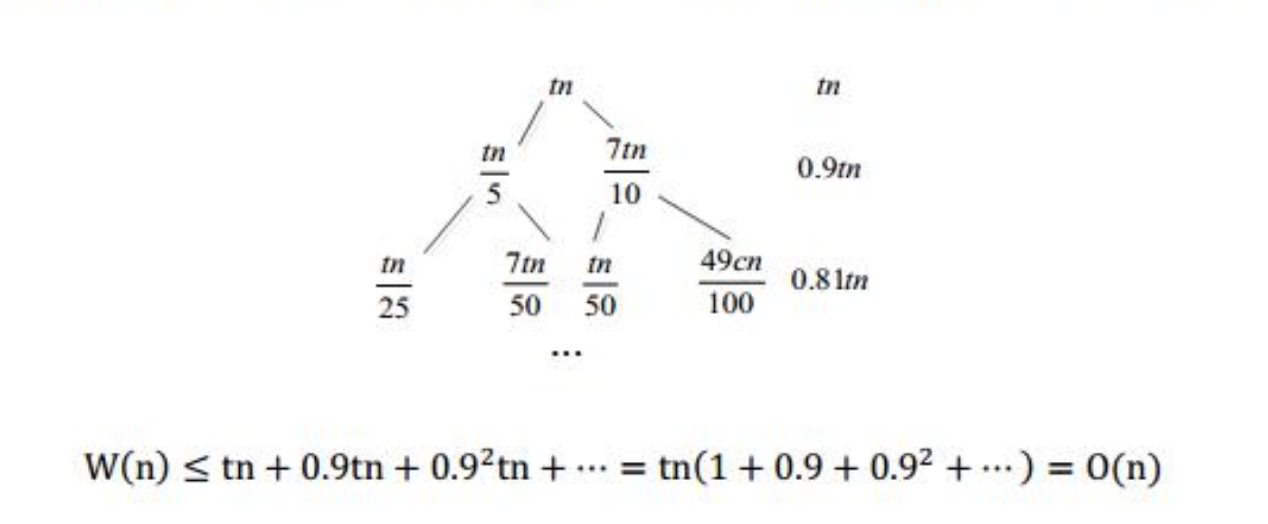
分析

在一番我看不懂的证明下推出来是\(O(n)\)。

源码

https://github.com/Sstee1XD/Algorithm_homework/tree/main/实验6 选第k小元素

#include <bits/stdc++.h>

using namespace std;

#define endl "\n"

const int N = 1e5 + 7;

int n, k;
int a[N], l[N], r[N], mid[N], tmp[N];

int gao(int a[], int n, int k) {
    if (n <= 5) { // 规模较小的问题直接输出答案
        sort(a, a + n);
        return a[k - 1];
    }
    int now = 0;
    for (int i = 0; i < n; i += 5) { // 分组找中位数
        if (i + 5 >= n) {
            sort(a + i, a + n, greater<int>());
            mid[now] = a[(n + i - 1) / 2];
            tmp[now++] = a[(n + i - 1) / 2];
        } else {
            sort(a + i, a + i + 5, greater<int>());
            mid[now] = a[i + 2];
            tmp[now++] = a[i + 2];
        }
    }
    
    
    for (int i = 0; i < now; ++i) { // 在中位数中找中位数
        int minn = tmp[i], minj = i;
        for (int j = i; j < now; ++j) {
            if (tmp[j] < minn) {
                minn = tmp[j];
                minj = j;
            }
        }
        if (minj != i) {
            int go = minn;
            tmp[minj] = tmp[i];
            tmp[i] = minn;
        }
    }

    int m = tmp[(now - 1) / 2];
    int nl = 0, nr = 0;
    for (int i = 0; i < now; ++i) {
        int sz = min(5, n - i * 5);
        int numBig = (sz + 1) / 2;
        int numSmall = sz - numBig;
        if (mid[i] == m) { // 中位数与m*相同，可以直接分
            if (numBig) {
                memcpy(r + nr, a + i * 5, numBig * sizeof(int));
                nr += numBig;
            }
            if (numSmall) {
                memcpy(l + nl, a + i * 5 + numBig, numSmall * sizeof(int));
                nl += numSmall;
            }
        } else if (mid[i] < m) { // 中位数小于m*，小的数字直接分，遍历大的
            for (int j = i * 5; j < i * 5 + numBig; ++j) {
                if (a[j] < m) l[nl++] = a[j];
                else r[nr++] = a[j];
            }
            if (numSmall) {
                memcpy(l + nl, a + i * 5 + numBig, numSmall * sizeof(int));
                nl += numSmall;
            }
        } else { // 中位数大于m*，大的直接分，遍历小的
            memcpy(r + nr, a + i * 5, numBig * sizeof(int));
            nr += numBig;
            for (int j = i * 5 + numBig; j < min(i * 5 + 5, n); ++j) {
                if (a[j] < m) l[nl++] = a[j];
                else r[nr++] = a[j];
            }
        }
    }
    if (nl == k - 1) return m; // m*就是第k小的数
    if (nl >= k) return gao(l, nl, k); // 第k小的数在小的序列里
    else return gao(r, nr, k - nl); // 第k小的数在大的序列里
}

void solve() {
    cin >> n >> k;
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
    }
    cout << gao(a, n, k) << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);cout.tie(nullptr);
    int t = 1;
    while (t--) solve();
    return 0;
}