算法实践2-2 Dijkstra

问题：

对于下图使用\(Dijkstra\)算法求由顶点\(a\)到顶点\(h\)的最短路径，按实验报告模板编写算法。

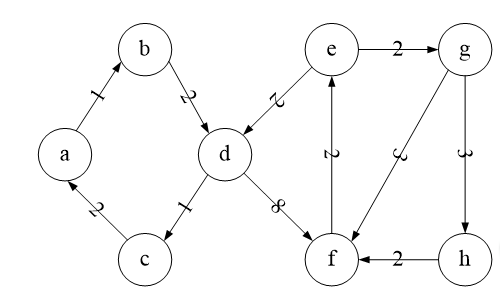
解析

我们从一个源点\(S\)出发，要找它到点\(T\)的最短距离，可以考虑将和源点相邻的点都放到我们的一个决策集合里。然后我们每次贪心地拿出到距离点\(S\)距离最近的点\(u\)，然后遍历跟点\(u\)相邻的点\(v\)，如果原先点\(v\)到点\(S\)的距离大于点\(u\)到点\(S\)的距离加上点\(u\)到点\(v\)的距离，那么我们就可以更新点\(v\)到点\(S\)的距离，同时也把点\(v\)加入我们的决策集合里，待到下一次选择点时，也将其纳入考虑的范围。当我们在决策集合中选择到点\(T\)时结束。

设计

void Dijkstra(int s, int t) {
    建立决策集合q
    将点s放入q中
    while (q不为空) {
        取出距离点s最近的点u
        if (u == t) return;
        for (遍历和u相邻的点v) {
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                将点v加入q中
            }
        }
    }
}

分析

需要遍历所有边，时间复杂度为\(O(e)\)。再加上用堆优化我们的决策集合，维护决策集合的时间复杂度为\(O(logn)\)。维护决策集合需要在遍历边的里面完成，所以总时间复杂度为\(O(elogn)\)。

源码

https://github.com/Sstee1XD/Algorithm_homework/tree/main/实验2-2 Dijkstra

#include <bits/stdc++.h>

using namespace std;

const int inf = 0x3f3f3f3f;
const int N = 1e2 + 7;

struct Edge {
    int nxt, v, w;

    Edge () {}
    Edge (int nxt, int v, int w) : nxt(nxt), v(v), w(w) {}
}edge[(N * N + N) << 1];

struct qnode {
    int u, w;

    bool operator < (const qnode &a) const {
        return w > a.w;
    }

    qnode () {}
    qnode (int u, int w) : u(u), w(w) {}
};

int dis[N], head[N], vis[N];
int n, m, u, v, w, tot, s, t;

void addedge(int u, int v, int w) {
    edge[tot] = Edge(head[u], v, w);
    head[u] = tot++;
}

void Dijkstra(int s, int t) {
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    dis[s] = 0;
    priority_queue<qnode> q;
    q.push(qnode(s, 0));
    while (!q.empty()) {
        int u = q.top().u;
        q.pop();
        if (vis[u]) continue;
        vis[u] = 1;
        if (u == t) return;
        for (int i = head[u]; ~i; i = edge[i].nxt) {
            int v = edge[i].v, w = edge[i].w;
            
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                q.push(qnode(v, dis[v]));
            }
        }
    }
}

int main() {
    tot = 0;
    memset(head, -1, sizeof(head));
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= m; ++i) {
        getchar();
        scanf("%c %c %d", &u, &v, &w);
        u -= 'a';
        v -= 'a';
        addedge(u, v, w);
    }
    getchar();
    scanf("%c %c", &s, &t);
    s -= 'a';
    t -= 'a';
    
    Dijkstra(s, t);
    printf("%d\n", dis[t]);
    return 0;
}
/*
8 11
a b 1
b d 2
c a 2
d c 1
d f 8
e d 2
e g 2
f e 2
g f 3
g h 3
h f 2
a h
*/