算法实践2-1 Floyd

问题：

用Floyd算法求解下图各个顶点的最短距离。写出Floyd算法的伪代码和给出距离矩阵（顶点之间的最短距离矩阵），按实验报告模板编写算法。

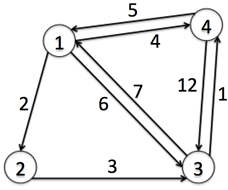
解析

点\(u\)到点\(v\)有两种方案可以走，一种是点\(u\)直接到点\(v\)，一种是通过中间点\(k\)，点\(u\)先到点\(k\)，再从点\(k\)走到点\(v\)。然后我们枚举中间点，再枚举起点和终点，进行更新。注意中间点要放在第一维，这样子只能达到通过一个中间点的效果，放在外面可以用通过中间点之后的状态来继续更新别的点之间的距离。

设计

void Floyd() {
    for (枚举中间点k) {
        for (枚举起点i) {
            for (枚举终点j) {
                若i到k的距离加上k到j的距离小于i到j的距离，进行更新
            }
        }
    }
}

分析

套了三个遍历点的\(for\)，时间复杂度为\(O(n^3)\)

源码

https://github.com/Sstee1XD/Algorithm_homework/tree/main/实验2-1 Floyd

#include <bits/stdc++.h>

using namespace std;

const int inf = 0x3f3f3f3f;
const int N = 1e2 + 7;

int dis[N][N];
int n, m, u, v, w;

void Floyd() {
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
            }
        }
    }
}

int main() {
    memset(dis, 0x3f, sizeof(dis));
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; ++i) dis[i][i] = 0;
    for (int i = 1; i <= m; ++i) {
        scanf("%d %d %d", &u, &v, &w);
        dis[u][v] = w;
    }
    Floyd();
    puts("");
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            printf("%d%c", dis[i][j], " \n"[j == n]);
        }
    }
    return 0;
}
/*
4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12
*/