机器学习实战 - 读书笔记(06) – SVM支持向量机

机器学习实战 - 读书笔记(06) – SVM支持向量机

前言

最近在看Peter Harrington写的“机器学习实战”，这是我的学习笔记，这次是第6章：SVM 支持向量机。
支持向量机不是很好被理解，主要是因为里面涉及到了许多数学知识，需要慢慢地理解。我也是通过看别人的博客理解SVM的。
推荐大家看看on2way的SVM系列：

• 解密SVM系列（一）：关于拉格朗日乘子法和KKT条件
• 解密SVM系列（二）：SVM的理论基础
• 解密SVM系列（三）：SMO算法原理与实战求解
• 解密SVM系列（四）：SVM非线性分类原理实验

基本概念

• SVM - Support Vector Machine。支持向量机，其含义是通过支持向量运算的分类器。其中“机”的意思是机器，可以理解为分类器。
  什么是支持向量呢？在求解的过程中，会发现只根据部分数据就可以确定分类器，这些数据称为支持向量。
  见下图，在一个二维环境中，其中点R，S，G点和其它靠近中间黑线的点可以看作为支持向量，它们可以决定分类器，也就是黑线的具体参数。
  

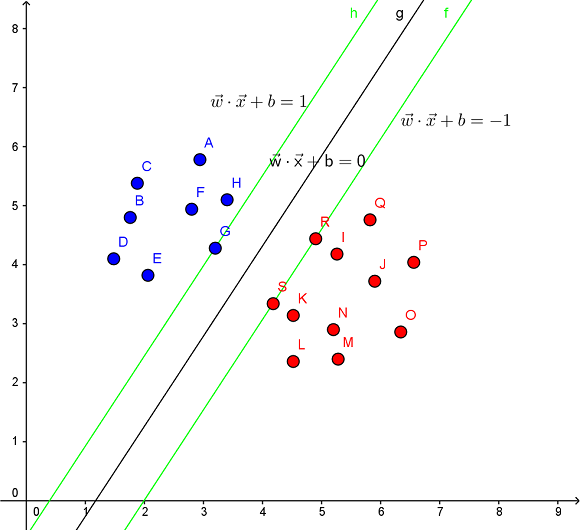
• 分类器：就是分类函数。

• 线性分类：可以理解为在2维空间中，可以通过一条直线来分类。在p维空间中，可以通过一个p-1维的超平面来分类。

• 向量：有多个属性的变量。在多维空间中的一个点就是一个向量。比如 \(x = (x_1, x_2, ..., x_n)\)。下面的\(w\)也是向量。

• 约束条件(subject to) ： 在求一个函数的最优值时需要满足的约束条件。

• 向量相乘: \(xw^T = \textstyle \sum_{i=1}^n w_ix_i\)

• 内积: \(\langle x,y \rangle = \textstyle \sum_{i=1}^n x_iy_i\)

解决的问题：

• 线性分类
  在训练数据中，每个数据都有n个的属性和一个二类类别标志，我们可以认为这些数据在一个n维空间里。我们的目标是找到一个n-1维的超平面（hyperplane），这个超平面可以将数据分成两部分，每部分数据都属于同一个类别。
  其实这样的超平面有很多，我们要找到一个最佳的。因此，增加一个约束条件：这个超平面到每边最近数据点的距离是最大的。也成为最大间隔超平面（maximum-margin hyperplane）。这个分类器也成为最大间隔分类器（maximum-margin classifier）。
  支持向量机是一个二类分类器。

• 非线性分类
  SVM的一个优势是支持非线性分类。它结合使用拉格朗日乘子法和KKT条件，以及核函数可以产生非线性分类器。

• 分类器1 - 线性分类器
  是一个线性函数，可以用于线性分类。一个优势是不需要样本数据。
  classifier 1:

\[f(x) = xw^T + b \]

\(w\) 和 \(b\) 是训练数据后产生的值。

• 分类器2 - 非线性分类器
  支持线性分类和非线性分类。需要部分样本数据（支持向量），也就是\(\alpha_i \ne 0\)的数据。
  \(\because\)
  \(w = \textstyle \sum_{i=1}^n \alpha_iy_ix_i\)
  \(\therefore\)
  classifier 2:

\[f(x) = \textstyle \sum_{i=1}^n \alpha_iy_i K(x_i, x) + b \\ \text{here} \\ \qquad x_i \text{ : training data i} \\ \qquad y_i \text{ : label value of training data i} \\ \qquad \alpha_i \text{ : Lagrange multiplier of training data i} \\ \qquad K(x_1, x_2) = exp(-\frac{\lVert x_1 - x_2 \rVert ^2}{2\sigma^2}) \text{ : kernel function} \\ \]

\(\alpha\), \(\sigma\) 和 \(b\) 是训练数据后产生的值。
可以通过调节\(\sigma\)来匹配维度的大小，\(\sigma\)越大，维度越低。

核心思想

• SVM的目的是要找到一个线性分类的最佳超平面 \(f(x) = xw^T + b = 0\)。求 \(w\) 和 \(b\)。
• 首先通过两个分类的最近点，找到\(f(x)\)的约束条件。
• 有了约束条件，就可以通过拉格朗日乘子法和KKT条件来求解，这时，问题变成了求拉格朗日乘子\(\alpha_i\) 和 \(b\)。
• 对于异常点的情况，加入松弛变量\(\xi\)来处理。
• 使用SMO来求拉格朗日乘子\(\alpha_i\)和\(b\)。这时，我们会发现有些\(\alpha_i = 0\)，这些点就可以不用在分类器中考虑了。
• 惊喜! 不用求\(w\)了，可以使用拉格朗日乘子\(\alpha_i\)和\(b\)作为分类器的参数。
• 非线性分类的问题：映射到高维度、使用核函数。

详解

线性分类及其约束条件

SVM的解决问题的思路是找到离超平面的最近点，通过其约束条件求出最优解。

对于训练数据集T，其数据可以分为两类C1和C2。
对于函数：\(f(x) = xw^T + b\)
对于C1类的数据 \(xw^T + b \geqslant 1\)。其中至少有一个点\(x_i\)， \(f(x_i) = 1\)。这个点称之为最近点。
对于C2类的数据 \(xw^T + b \leqslant -1\)。其中至少有一个点\(x_i\)， \(f(x_i) = -1\)。这个点称也是最近点。
上面两个约束条件可以合并为：
\(y_if(x_i) = y_i(x_iw^T + b) \geqslant 1\)。
\(y_i\)是点\(x_i\)对应的分类值（-1或者1）。
求\(w\)和\(b\).
则超平面函数是\(xw^T + b = 0\)。
为了求最优的f(x)， 期望训练数据中的每个点到超平面的距离最大。
（解释1: 这里需要理解一个事情，根据上图，我们可以给每个点做一条平行于超平面的平行线（超平行面），因此，这个最大化相当于求最近点到超平面距离的最大化。）

总结，现在我们的公式是：
Formula 6.1

\[f(x) = xw^T + b \\ \text{subject to} \\ \qquad y_if(x_i) = y_i(x_iw^T + b) \geqslant 1, i = 1, ..., n \]

几个训练脑筋的小问题：

• Q: y是否可以是其它非{-1， 1}的值?
  A: 将y值定义为{-1， 1}是最简化的方案。你的分类可以是cat和dog，只要将cat对应到1, dog对应到-1就可以了。你也可以将y值定义为其它数比如: -2, 2或者2, 3之类的，但是这样就需要修改超平面函数和约束条件，增加了没必要的繁琐，实际上和y值定义为{-1， 1}是等价的。

• Q: 如果两组数据里的太近或者太远，是不是可能就找不到\(xw^T + b = 1\) 和\(xw^T + b = -1\)的这两个点？
  A: 不会。假设可以找到\(x_iw^T + b = c\) 和 \(x_jw^T + b = -c\). \(c > 0 and c <> 1\)。其超平面函数为\(xw^T + b = 0\).
  上面公式左右同时除以c, 则：
  \(x_iw^T / c + b / c = 1\)
  \(x_jw^T / c + b / c = -1\)
  令:
  \(w' = w/c\)
  \(b' = b/c\)
  有:
  \(x_iw'^T + b' = 1\)
  \(x_jw'^T + b' = -1\)
  可以找到超平面函数:
  \(xw^T + b' = 0\)
  因此，总是可以找到y是{-1, 1}的超平面，如果有的话。

最大几何间隔（geometrical margin）

\(f(x)\)为函数间隔\(\gamma\)。
如果求\(\text{max } yf(x)\)，有个问题，就是w和b可以等比例增大，导致\(yf(x)\)的间隔可以无限大。因此需要变成求等价的最大几何间隔：

\[\bar{\gamma} = \frac{yf(x)}{\lVert w \rVert} \\ \text{subject to} \\ \qquad y_if(x_i) = y_i(x_iw^T + b) \geqslant 1, i = 1, ..., n \]

\(\lVert w \rVert\) : 二阶范数，也就是各项目平方和的平方根。 \(\sqrt {\textstyle \sum_{i=1}^n w_i^2}\)

根据上面的解释，这个问题可以转变为：

\[\text{max } \frac{1}{\lVert w \rVert} \\ \text{subject to} \\ \qquad y_i(x_iw^T + b) \geqslant 1, i = 1, ..., n \]

再做一次等价转换：
Formula 6.2

\[\text{min } \frac{1}{2} \lVert w \rVert ^ 2 \\ \text{subject to} \\ \qquad y_i(x_iw^T + b) \geqslant 1, i = 1, ..., n \]

求解问题\(w,b \Leftrightarrow \alpha_i, b\)

我们使用拉格朗日乘子法和KKT条件来求\(w\)和\(b\)，一个重要原因是使用拉格朗日乘子法后,还可以解决非线性划分问题。
拉格朗日乘子法和KKT条件可以解决下面这个问题：

1. 求一个最优化问题 \(f(x)\)
   刚好对应我们的问题：\(min \frac{1}{2} \lVert w \rVert ^ 2\)
2. 如果存在不等式约束\(g_k(x) <= 0, k = 1, …, q\)。
   对应 \(\text{subject to } \qquad 1 - y_i(x_iw^T + b) <= 0, i = 1, ..., n\)
3. F(x)必须是凸函数。这个也满足。

SVM的问题满足使用拉格朗日乘子法的条件。因此问题变成：
Formula 6.3

\[\underset{\alpha}{max} \text{ } W(\alpha) = \mathcal{L}(w,b,\alpha) = \frac{1}{2} \lVert w \rVert ^ 2 - \textstyle \sum_{i=1}^n \alpha_i(y_i(x_iw^T + b) - 1) \\ \text{subject to} \\ \qquad \alpha_i >= 0, i = 1, ..., n \\ \qquad \textstyle \sum_{i=1}^n \alpha_iy_i = 0 \\ \qquad 1 - y_i(x_iw^T + b) <= 0, i = 1, ..., n \\ \qquad w = \textstyle \sum_{i=1}^n \alpha_iy_ix_i \\ \text{here} \\ \qquad \alpha_i \text{ : Lagrange multiplier of training data i} \\ \]

消除\(w\)之后变为：
Formula 6.4

\[\underset{\alpha}{max} \text{ } W(\alpha) = \mathcal{L}(w,b,\alpha) = \textstyle \sum_{i=1}^n \alpha_i - \frac{1}{2} \textstyle \sum_{i,j=1}^n \alpha_i\alpha_jy_iy_jx_i^Tx_j \\ \text{subject to} \\ \qquad \alpha_i >= 0, i = 1, ..., n \\ \qquad \textstyle \sum_{i=1}^n \alpha_iy_i = 0 \\ \qquad \alpha_i(1 - y_i(\textstyle \sum_{j=1}^n \alpha_jy_j \langle x_j,x_i \rangle + b)) = 0, i = 1, ..., n \]

\(\langle x_j,x_i \rangle\)是\(x_j\) 和 \(x_i\)的内积，相当于\(x_ix_j^T\)。
可见使用拉格朗日乘子法和KKT条件后，求\(w,b\)的问题变成了求拉格朗日乘子\(\alpha_i\)和\(b\)的问题。
到后面更有趣，变成了不求\(w\)了，因为\(\alpha_i\)可以直接使用到分类器中去，并且可以使用\(\alpha_i\)支持非线性的情况（\(xw^T + b\)是线性函数，支持不了非线性的情况哦）。

以上的具体证明请看：
解密SVM系列（二）：SVM的理论基础
关于拉格朗日乘子法和KKT条件，请看：
深入理解拉格朗日乘子法（Lagrange Multiplier)和KKT条件

处理异常点（outliers）

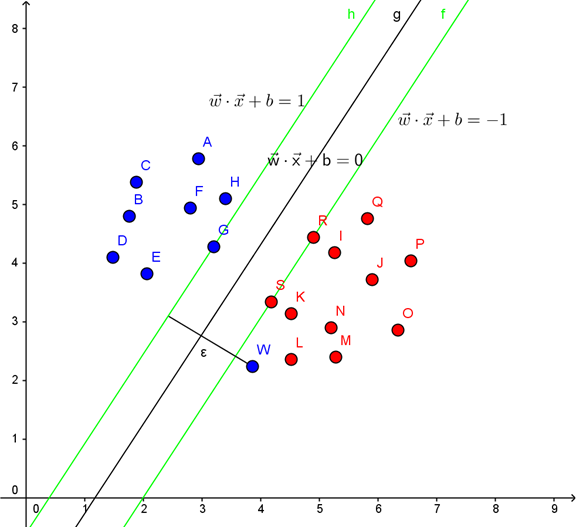
如上图：点w是一个异常点，导致无法找到一个合适的超平面，为了解决这个问题，我们引入松弛变量(slack variable)\(\xi\)。
修改之间的约束条件为：\(x_iw^T + b >= 1 – \xi_i \qquad \text{for all i = 1, …, n}\)
则运用拉格朗日乘子法之后的公式变为：
Formula 6.5

\[\underset{\alpha}{max} \text{ } W(\alpha) = \mathcal{L}(w,b,\alpha) = \textstyle \sum_{i=1}^n \alpha_i - \frac{1}{2} \textstyle \sum_{i,j=1}^n \alpha_i\alpha_jy_iy_jx_jx_i^T \\ \text{subject to} \\ \qquad 0 \leqslant \alpha_i \leqslant C, i = 1, ..., n \\ \qquad \textstyle \sum_{i=1}^n \alpha_iy_i = 0 \\ \qquad \alpha_i(1 - y_i(\textstyle \sum_{j=1}^n \alpha_jy_j \langle x_j,x_i \rangle + b)) = 0, i = 1, ..., n \]

输入参数：

• 参数\(C\)，越大表明影响越严重。\(C\)应该一个大于0值。其实\(C\)也不能太小，太小了就约束\(\alpha_i\)了，比如200。
• 参数\(\xi\)，对所有样本数据起效的松弛变量，比如：0.0001。
  具体证明请看：
  解密SVM系列（二）：SVM的理论基础

求解\(\alpha\) - 使用SMO方法

1996年，John Platt发布了一个称为SMO的强大算法，用于训练SVM。SMO表示序列最小优化（Sequential Minimal Optimization）。
SMO方法：
概要：SMO方法的中心思想是每次取一对\(\alpha_i\)和\(\alpha_j\)，调整这两个值。
参数: 训练数据/分类数据/\(C\)/\(\xi\)/最大迭代数
过程：

初始化\(\alpha\)为0；
在每次迭代中 （小于等于最大迭代数），
- 找到第一个不满足KKT条件的训练数据，对应的\(\alpha_i\)，
- 在其它不满足KKT条件的训练数据中，找到误差最大的x，对应的index的\(\alpha_j\)，
- \(\alpha_i\)和\(\alpha_j\)组成了一对，根据约束条件调整\(\alpha_i\), \(\alpha_j\)。

不满足KKT条件的公式：
Formula 6.6

\[\text{(1) } y_i(u_i - y_i) \leqslant \xi \text{ and } \alpha_i < C \\ \text{(2) } y_i(u_i - y_i) \geqslant \xi \text{ and } \alpha_i > 0 \\ here \\ \qquad u_i = \textstyle \sum_{j=1}^n \alpha_jy_j K(x_j, x_i) + b \\ \qquad K(x_1, x_2) = \langle x_1, x_2 \rangle \\ \qquad \xi \text{ : slack variable} \]

调整公式：
Formula 6.7

\[\alpha_2^{new} = \alpha_2^{old} - \frac{y_2(E_1 - E_2)}{\eta} \\ \alpha_1^{new} = \alpha_1^{old} + y_1y_2(\alpha_2^{old} - \alpha_2^{new}) \\ b_1 = b^{old} - E_1 -y_1(\alpha_1^{new} - \alpha_1^{old})K(x_1, x_1) - y_2(\alpha_2^{new} - \alpha_2^{old})K(x_1, x_2) \\ b_2 = b^{old} - E_2 -y_1(\alpha_1^{new} - \alpha_1^{old})K(x_1, x_2) - y_2(\alpha_2^{new} - \alpha_2^{old})K(x_2, x_2) \\ b = \begin{cases} b_1 & \text{if } 0 \leqslant \alpha_1^{new} \leqslant C \\ b_2 & \text{if } 0 \leqslant \alpha_2^{new} \leqslant C \\ \frac{b_1 + b_2}{2} & \text{otherwise} \end{cases} \\ here \\ \qquad E_i = u_i - y_i \\ \qquad \eta = 2K(x_1, x_2) - K(x_1, x_1) - K(x_2, x_2) \\ \qquad u_i = \textstyle \sum_{j=1}^n \alpha_jy_j K(x_j, x_i) + b \\ \qquad K(x_1, x_2) = \langle x_1, x_2 \rangle \]

具体证明请参照:
解密SVM系列（三）：SMO算法原理与实战求解

最后一步：解决非线性分类

根据机器学习的理论，非线性问题可以通过映射到高维度后，变成一个线性问题。
比如：二维下的一个点\(<x1, x2>\), 可以映射到一个5维空间，这个空间的5个维度分别是:\(x1, x2, x1x2, x1^2, x2^2\)。
映射到高维度，有两个问题：一个是如何映射？另外一个问题是计算变得更复杂了。
幸运的是我们可以使用核函数(Kernel function)来解决这个问题。
核函数(kernel function)也称为核技巧(kernel trick)。
核函数的思想是：

仔细观察Formula 6.6 和 Formula 6.7，就会发现关于向量\(x\)的计算，总是在计算两个向量的内积\(K(x_1, x_2) = \langle x_1, x_2 \rangle\)。
因此，在高维空间里，公式的变化只有计算低维空间下的内积\(\langle x_1, x_2 \rangle\)变成了计算高维空间下的内积\(\langle x'_1, x'_2 \rangle\)。
核函数提供了一个方法，通过原始空间的向量值计算高维空间的内积，而不用管映射的方式。
我们可以用核函数代替\(K(x_1, x_2)\)。

核函数有很多种, 一般可以使用高斯核（径向基函数（radial basis function））
Formula 6.8

\[K(x_1, x_2) = exp(-\frac{\lVert x_1 - x_2 \rVert ^2}{2\sigma^2}) \]

可以通过调节\(\sigma\)来匹配维度的大小，\(\sigma\)越大，维度越低，比如10。
可以参照：
解密SVM系列（四）：SVM非线性分类原理实验
支持向量机通俗导论（理解SVM的三层境界）

如何解决多类分类问题

支持向量机是一个二类分类器。基于SVM如何构建多类分类器，建议阅读C. W. Huset等人发表的一篇论文"A Comparison of Methods for Multiclass Support Vector Machines"。需要对代码做一些修改。

参照

• Machine Learning in Action by Peter Harrington
• 解密SVM系列（一）：关于拉格朗日乘子法和KKT条件
• 解密SVM系列（二）：SVM的理论基础
• 解密SVM系列（三）：SMO算法原理与实战求解
• 解密SVM系列（四）：SVM非线性分类原理实验
• 深入理解拉格朗日乘子法（Lagrange Multiplier)和KKT条件
• 支持向量机通俗导论（理解SVM的三层境界）
• https://en.wikipedia.org/wiki/Support_vector_machine