方差学习总结
在分析之前，要严格区分一个概念是在概率学上的定义还是在统计学上的定义。概率学比统计学更加的抽象一点，概率学研究一个事件的理想的情况，但是在真实的世界，这种理想的情况是很难或者不可能达到的，所以利用统计学中的样本来估计这个理想的结果。
方差的概念和定义
概率论中方差用来度量随机变量和其数学期望（均值）之间的偏离程度。
统计学中的方差（样本方差）是各个数据分别与其平均数之差的平方和的平均数。
设X是一个随机变量，若$E\{ {[X - E(X)]^2}\} $存在，则称$E\{ {[X - E(X)]^2}\} $为X的方差，记为D(X)或者Var(X)。
D(X)是刻画X取值分散程度的一个量，它是衡量取值分散程度的一个尺度。
方差的种类与计算
离散型方差：
$D(x) = \sum\nolimits_{i = 1}^n {{p_i} \cdot {{({x_i} - u)}^2}} $。其中$u = E(x) = \sum\nolimits_{i = 1}^n {{p_i} \cdot {x_i}} $
注意：在统计学中，样本的均值为$\widehat u = \frac{1}{n}\sum\nolimits_{i = 1}^n {{x_i}} $
将上面的D(x)展开后得到\[D(x) = Var(x) = \sum\nolimits_{i = 1}^n {({p_i} \cdot x_i^2) - {u^2}} \]
连续型方差：
对于连续型随机变量，$Var(x) = {\sigma ^2} = \int {{{(x - u)}^2}f(x)dx = } \int {{x^2}f(x)dx - {u^2}} $其中$u = \int {xf(x)dx} $并且此处的积分是以x的取值范围（一般是负无穷~正无穷）为积分上下界的定积分。所以$\int_{ - \infty }^{ + \infty } {f(x)dx} = 1$。
根据方差的定义：$D(x) = E\{ {[X - E(X)]^2}\} $
所以：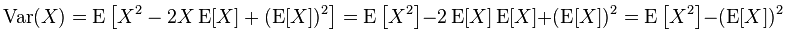
方差的特性
重点分布的方差
统计学中的样本方差
方差是各个数据与平均值之差的平方和的平均数，即：
\[{s^2} = \frac{1}{n}[{({x_1} - \overline x )^2} + {({x_2} - \overline x )^2} + ... + {({x_n} - \overline x )^2}]\]
其中$\overline x $是样本的平均数。
注意这里的${s^2}$并不是随机变量的方差，它是利用样本数据对随机变量方差的一个估计。
现在样本只是总体的一部分，用样本得到的样本方差也不可能那么理想的正好等于总体方差。为了能准确的估计总体方差，希望这个样本方差能够是总体方差的一个无偏估计。也就是说$E({s^2}) = {\sigma ^2}$。其中${s^2}$是样本方差，${\sigma ^2}$是总体方差。
但是上面的${s^2}$不是${\sigma ^2}$的无偏估计：
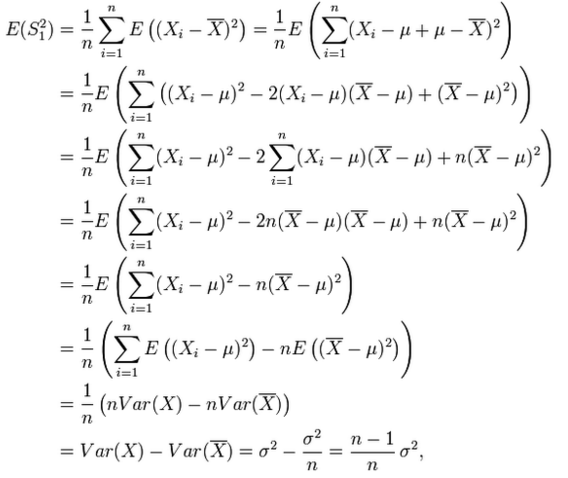
从公式推导可以看到，这里的${s^2}$不是${\sigma ^2}$的无偏估计。
所以一般的样本方差用一个修正值：
\[{s^2} = \frac{1}{{n - 1}}{\sum\nolimits_{i = 1}^n {({X_i} - \overline X )} ^2}\]
对上面的公式做一个解释
样本方差公式里分母为n-1的目的是为了让方差的估计无偏，因为无偏的估计比有偏估计更好的符合直觉。尽管有的统计学家认为让mean square error即MSE最小才更具有意义。
在做出解释前先给出结论：
\[E[\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{({X_i} - \overline X )}^2}} ] = {\sigma ^2}\]
也就是说$\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{({X_i} - \overline X )}^2}} $是总体样本方差${\sigma ^2}$的无偏估计。
第一种情况：
假设随机变量X的数学期望u是已知的，然而${\sigma ^2}$是未知的。在这种情况下，样本方差可以直接用定义写出来：各个数据分别与平均数（这里的平均数是均值u）之差的平方和的平均数。也就是：${s^2} = \frac{1}{n}{\sum\nolimits_{i = 1}^n {({X_i} - u)} ^2}$。
\[\begin{array}{l}E({s^2})\\ = E(\frac{1}{n}{\sum\nolimits_{i = 1}^n {({X_i} - u)} ^2})\\ = \frac{1}{n}E({\sum\nolimits_{i = 1}^n {({X_i} - u)} ^2})\\ = \frac{1}{n}{\sum\nolimits_{i = 1}^n {E[({X_i} - u)} ^2}]\\ = \frac{1}{n}\sum\nolimits_{i = 1}^n {E[{X_i}^2 - 2u} {X_i} + {u^2}]\\ = \frac{1}{n}\sum\nolimits_{i = 1}^n {[E{X_i}^2 - 2uE{X_i} + {u^2}]} \\ = \frac{1}{n}\sum\nolimits_{i = 1}^n {[{\sigma ^2} + {u^2} - 2{u^2} + {u^2}]} \\ = {\sigma ^2}\end{array}\]
所以$E(\frac{1}{n}{\sum\nolimits_{i = 1}^n {({X_i} - u)} ^2}) = {\sigma ^2}$
即在随机变量X的数学期望u已知的条件下，$\frac{1}{n}{\sum\nolimits_{i = 1}^n {({X_i} - u)} ^2}$是总体方差的无偏估计。
第二种情况：
在随机变量X的数学期望u未知的情况下，我们被迫使用样本均值 ${\overline X }$代替上面的u，也就是使用$\frac{1}{n}{\sum\nolimits_{i = 1}^n {({X_i} - \overline X )} ^2}$作为总体方差${{\sigma ^2}}$的估计。
但是这种情况往往会低估总体方差。因为：
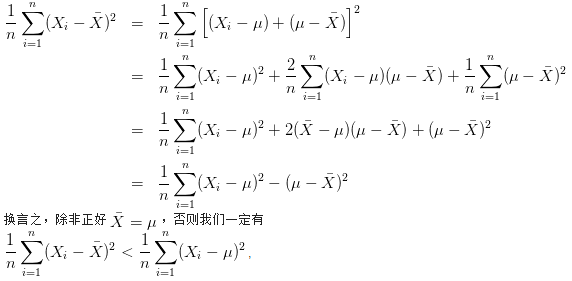
而$\frac{1}{n}{\sum\nolimits_{i = 1}^n {({X_i} - u)} ^2}$才是对总体方差的无偏估计。
综合上面的两种情况来说：
在不知道随机变量真实数学期望的条件下，把分母n换成n-1，就是把原来偏小的估计放大了一点，这样就能得到正确的估计了。
$E(\frac{1}{n}{\sum\nolimits_{i = 1}^n {({X_i} - u)} ^2}) = E[\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{({X_i} - \overline X )}^2}} ] = {\sigma ^2}$至于为什么是n-1，而不是n-2或者什么别的数，上面的公式已经推导过了。
一般化
