AtCoder Beginner Contest 426 ABCDEF 题目解析
A - OS Versions
题意
有三种操作系统的版本,按发布时间顺序分别为 Ocelot、Serval、Lynx。
给定字符串 \(X, Y\),请判断版本 \(X\) 相比于版本 \(Y\) 的发布时间是否相同或更靠后(版本相同或更新)。
思路
直接判断所有情况。或者将版本字符串转为数字 \(1, 2, 3\) 后再比较大小。
代码
int f(string s)
{
if(s == "Ocelot")
return 1;
if(s == "Serval")
return 2;
return 3;
}
void solve()
{
string x, y;
cin >> x >> y;
if(f(x) >= f(y))
cout << "Yes\n";
else
cout << "No\n";
}
B - The Odd One Out
题意
给你一个长度至少为 \(3\) 且仅由小写英文字母组成的字符串 \(S\)。
\(S\) 仅包含恰好两种类型的字符,且其中一种字符只出现了一次。
请找出这个只出现了一次的字符。
思路
用一个计数数组统计每种字符出现的次数,最后找哪种字符只出现了一次即可。
代码
int cnt[128];
void solve()
{
string s;
cin >> s;
for(char c : s)
cnt[c]++;
for(char c = 'a'; c <= 'z'; c++)
if(cnt[c] == 1)
{
cout << c;
return;
}
}
C - Upgrade Required
题意
某操作系统有 \(N\) 个版本,按发布的时间顺序编号为 \(1,2,\dots,N\) 。
共有 \(N\) 台个人电脑。第 \(i\) 台电脑一开始的操作系统版本为 \(i\)。
请按顺序执行 \(Q\) 次操作。第 \(i\) 次操作如下:
- 给定 \(X_i, Y_i\),对于所有操作系统版本为 \(X_i\) 或早于 \(X_i\) 的电脑,将其操作系统全部更新为 \(Y_i\)(\(X_i \lt Y_i\)),然后输出本次操作影响了多少台电脑。
思路
因为版本号只会往大变化,不会变小(\(X_i \lt Y_i\))。所以我们可以用变量来维护当前所有电脑中操作系统编号的最小值,暂时记作 \(t\)。再借助一个计数数组 \(cnt_i\) 来维护每种版本对应的电脑数量。一开始 \(cnt_i = 1\)。
只要接下来这个操作对应的 \(X_i\) 比当前所有操作系统版本的最小值 \(t\) 还要小,那么便可以直接判断不存在任何能够被修改的电脑,直接跳过这一次操作即可。
而如果接下来这个操作对应的 \(X_i\) 比当前所有操作系统版本的最小值 \(t\) 要大(或者相等),那么本次操作会影响到的版本号只存在于 \([t, X_i]\) 这段区间内,且操作结束后所有 \(\lt X_i\) 的版本就全都没有了,最小版本 \(t\) 将会变为 \(X_i+1\)。
所以对于每个版本,我们最多只会看一次对应的电脑数量。每次把版本在 \([t, X_i]\) 区间内的电脑数量求和后,加入到 \(cnt_{Y_i}\) 内即可。
时间复杂度 \(O(Q+N)\)。
代码
int cnt[1000005];
// cnt[i] 表示版本为 i 的电脑的数量
void solve()
{
int n, q;
cin >> n >> q;
for(int i = 1; i <= n; i++)
cnt[i] = 1;
int id = 1; // 目前存在的最小版本号
while(q--)
{
int x, y;
cin >> x >> y;
if(x < id) // x 小于目前存在的最小版本号,直接判定没有任何受影响的电脑
{
cout << 0 << "\n";
continue;
}
int sum = 0;
while(id <= x) // 把 [id, x] 范围内的 PC 版本均改为 y
{
sum += cnt[id];
cnt[id] = 0;
id++;
}
cnt[y] += sum;
cout << sum << "\n";
}
}
D - Pop and Insert
题意
给定一个长度为 \(N\) 的字符串 \(S\) ,字符串仅由 0 和 1 组成。
您可以对 \(S\) 执行以下操作任意次(可能为零次):
- 删除当前字符串的第一个或最后一个字符,将其翻转(将
0变为1或将1变为0)后再插入任意位置。
为了让 \(S\) 的所有字符全部相同,请求出所需的最少操作数。
思路
可以发现,不论我们把最终目标定为全 0 或者全 1,一定会有一段连续的字符是不会被操作到的。
然后,为了让其它字符都变成和这段字符相同,可以有以下讨论:
- 对于所有与当前这一段字符不同的那些字符,因为题目允许删除字符后随意插入,我们肯定是直接在对其 0/1 翻转后直接插入到当前这段字符中间。因此这些字符的操作次数为 \(1\) 次。
- 对于所有与当前这一段字符相同且不相邻的那些字符,首先因为不相邻,所以为了让中间那些不同字符都能被处理到,这些字符肯定是要被至少操作一次的。但又因为每次操作都会 0/1 翻转,为了再变回来,所以还得再操作一次(后面这一次操作可以直接参考上一条讨论)。所以这些字符的操作次数为 \(2\) 次。
假设我们想要让所有字符全部变为 0,那么符合上面讨论中“第一种”条件的字符就是字符 1 的个数,这是不变的。但为了让操作次数最少,只能让符合上面讨论中“第二种”条件的字符尽可能少,所以我们肯定会选择一开始连续的最长一段 0 予以保留。
如果想要让所有字符全部变为 1,同理。
所以我们的任务就是求出 0 和 1 每种字符出现的次数以及连续出现的最长一段的长度。
假设 \(cnt_{0/1}\) 表示数量,\(mx_{0/1}\) 表示连续出现的最长一段的长度。
如果最终希望全变为 0,则条件一的数量为 \(cnt_1\),条件二的数量为 \(cnt_0 - mx_0\),最少操作次数为 \(cnt_1 \times 1 + (cnt_0 - mx_0) \times 2\)。
如果最终希望全变为 1,最少操作次数则为 \(cnt_0 \times 1 + (cnt_1 - mx_1) \times 2\)。
两种情况取个最小值即可。
单组数据时间复杂度 \(O(N)\)。
代码
char s[500005];
void solve()
{
int n;
cin >> n >> s;
int cnt[2] = {0, 0}; // 0/1 分别出现了多少次
for(int i = 0; i < n; i++)
cnt[s[i] - '0']++;
int mx[2] = {0, 0}; // 0/1 分别出现的连续最多次数是多少次
for(int i = 0; i < n;)
{
int j = i;
while(s[j + 1] == s[i]) // 找最后一个 == s[i] 且与 i 连续的位置
j++;
mx[s[i] - '0'] = max(mx[s[i] - '0'], j - i + 1);
i = j + 1;
}
cout << min(cnt[1] + (cnt[0] - mx[0]) * 2, cnt[0] + (cnt[1] - mx[1]) * 2) << "\n";
}
int main()
{
int t;
cin >> t;
while(t--)
solve();
return 0;
}
E - Closest Moment
题意
高桥和青木在二维平面上行走。高桥的起点是 \((TS_X, TS_Y)\) ,目标点是 \((TG_X, TG_Y)\) 。青木的起点是 \((AS_X, AS_Y)\) ,目标点是 \((AG_X, AG_Y)\) 。
他们同时从各自的起点出发,并以 \(1\) 个单位距离每秒的速度向各自的目标点前进,到达各自的目标点后停止。(注意,他们是同时出发的,但不一定会同时停止)。
求在行走过程中(包括出发时和停止后),两人之间距离的最小值。
这里的距离指的是欧几里得距离。也就是说,两点 \((x_1,y_1),(x_2,y_2)\) 之间的距离定义为 \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\) 。
思路
由于两个人行进的速度相同,如果两人朝着各自对应的方向一直走的话,他们之间的距离变化情况只可能会出现三种:一直变大、一直变小、先变小后变大。下文记该部分为情况一。
而如果两人中的某人停了下来,另一个人继续走,那么问题就变成了求平面内一个固定点到一条线段的最短距离。此时随着可以走的那个人在线段上继续移动,两人之间的距离也只有和上面一样的三种情况:一直变大、一直变小、先变小后变大。下文记该部分为情况二。
对于情况二,可以借助计算几何的方式,先求点到线段端点的距离,如果存在“先变小后变大”的情况,可以采取作垂线求交点再取垂线长度的方式解题。
对于这两种情况,如果在过程中出现的是“一直变大”或者“一直变小”的情况,可以借助浮点型二分法帮我们快速找到最佳答案的近似解。但对于“先变小后变大”这种情况,答案的变化不具有单调性,而是满足一个开口朝上的二次函数形式。在形似二次函数的变化曲线上找最值,可以采用三分法。
需要注意的是,情况一与情况二不能结合起来一起三分,因为有可能在情况一中出现“先变小后变大”的情况,在变大的途中忽然某个人因为走到了终点而停下来,来到情况二,然后又出现“先变小后变大”的情况。所以两部分应当分开计算,各自进行一次三分。
例子如下,A B 在移动过程中的距离变化呈现“先变小再变大再变小再变大”的情形:
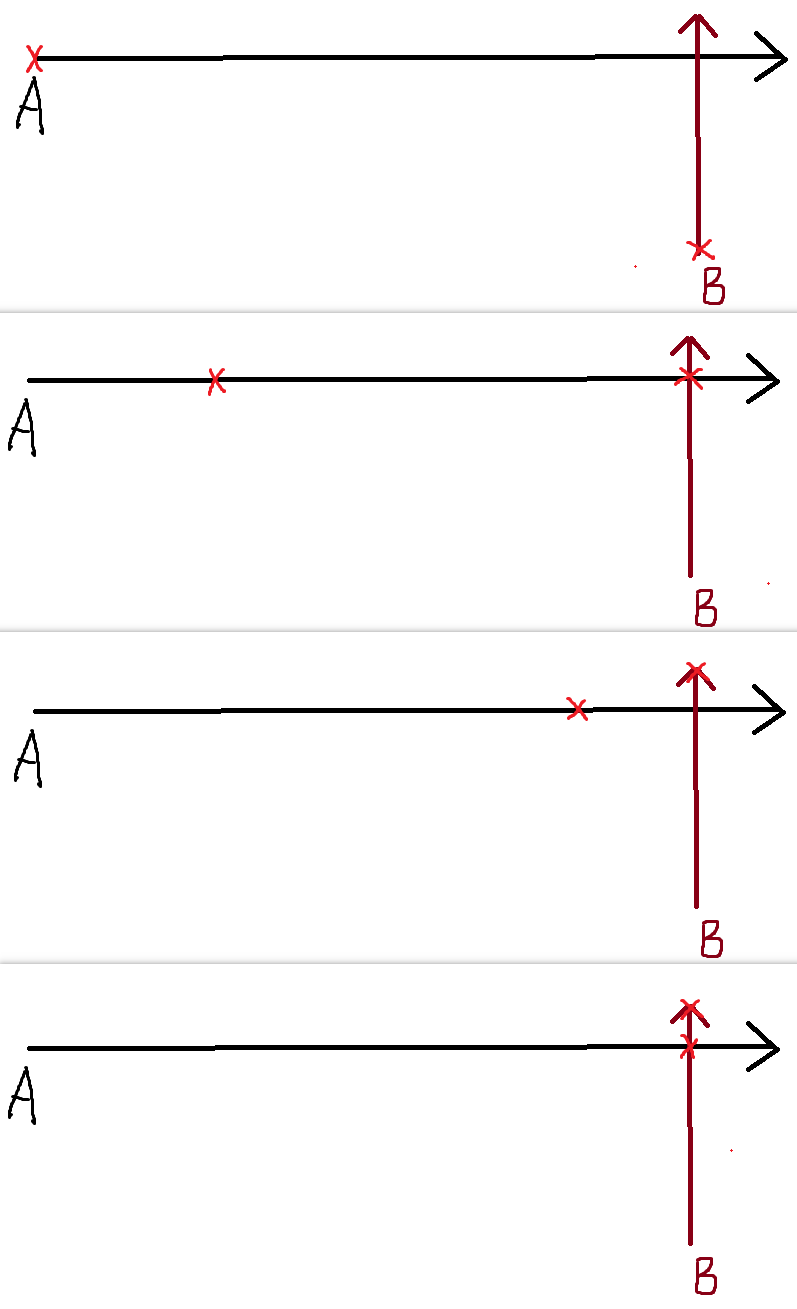
单组数据时间复杂度取决于设置的三分次数,约 \(O(\log D)\),其中 \(D\) 与两人行进距离有关。
代码
const double eps = 1e-10; // 设定给三分的极小值
struct Point
{
double x, y;
Point(){}
Point(double _x, double _y)
{
x = _x, y = _y;
}
};
typedef Point Vector;
Point sa, ta, sb, tb;
Vector va, vb; // a b 两人的单位方向向量
double disa, disb; // a b 两人的总移动距离
// 两点距离
double distance(Point a, Point b)
{
double dx = a.x - b.x, dy = a.y - b.y;
return sqrt(dx * dx + dy * dy);
}
// 计算走 tim 秒后两人的距离
double cal(double tim)
{
Point pa, pb;
if(tim >= disa)
pa = ta;
else
pa = Point(sa.x + tim * va.x, sa.y + tim * va.y);
if(tim >= disb)
pb = tb;
else
pb = Point(sb.x + tim * vb.x, sb.y + tim * vb.y);
return distance(pa, pb);
}
void solve()
{
cin >> sa.x >> sa.y;
cin >> ta.x >> ta.y;
cin >> sb.x >> sb.y;
cin >> tb.x >> tb.y;
disa = distance(sa, ta);
disb = distance(sb, tb);
// 两者移动方向的单位向量
va = Vector((ta.x - sa.x) / disa, (ta.y - sa.y) / disa);
vb = Vector((tb.x - sb.x) / disb, (tb.y - sb.y) / disb);
double ans = min(cal(0), min(cal(disa), cal(disb)));
// 等长线段移动部分,三分
double l = 0, r = min(disa, disb);
while(r - l > eps)
{
double mid1 = (l + l + r) / 3;
double mid2 = (l + r + r) / 3;
double dis1 = cal(mid1);
double dis2 = cal(mid2);
if(dis1 >= dis2)
l = mid1;
else
r = mid2;
}
ans = min(ans, cal((l + r) / 2));
// 一人停止,一人移动,点到线段最短距离,三分
l = min(disa, disb), r = max(disa, disb);
while(r - l > eps)
{
double mid1 = (l + l + r) / 3;
double mid2 = (l + r + r) / 3;
double dis1 = cal(mid1);
double dis2 = cal(mid2);
if(dis1 >= dis2)
l = mid1;
else
r = mid2;
}
ans = min(ans, cal((l + r) / 2));
cout << fixed << setprecision(15) << ans << "\n";
}
int main()
{
int t;
cin >> t;
while(t--)
solve();
return 0;
}
F - Clearance
题意
有 \(N\) 种产品,第 \(i\) 种产品一开始的库存有 \(A_i\) 件。
请依次处理以下 \(Q\) 个订单。第 \(i\) 个订单如下:
- 给定 \(l_i, r_i, k_i\),对于所有编号范围在区间 \([l_i, r_i]\) 内的产品,每种均购买 \(k_i\) 件(如果库存剩余不足 \(k_i\) 件,则全部买完),最后输出这个订单总共买到了多少件产品。
思路
由于每次需要处理一整段区间的产品,可以考虑采用线段树。对于区间整体而言,我们可以把内部的物品分为“至少 \(k_i\) 件”、“不足 \(k_i\) 件但还没用完”、“已用完”三类。
记 \(cnt\) 表示区间内未用完的产品数量,如果区间内部不存在任何一件产品的剩余数量在 \([1, k_i-1]\) 之间的话,那么这段区间对答案的贡献就可以直接通过 \(cnt \times k_i\) 来获得。那么为了判断是否区间内部存在某件没用完的产品的剩余数量小于 \(k_i\),我们还可以再维护一个区间最小值 \(minn\)。
如果区间内不存在“不足 \(k_i\) 件但还没用完”的产品,那么线段树在查询到子区间对应结点时便可以直接返回 \(cnt \times k_i\) 作为答案,然后在当前结点打上“整体减少 \(k_i\) 件”的懒惰标记;而如果区间内存在“不足 \(k_i\) 件但还没用完”的产品,我们则需要将这类产品进行单独处理,将其对未用完的产品数量 \(cnt\) 以及区间最小值 \(minn\) 的影响消除。而在消除影响时,对于 \(cnt\) 而言要改为 \(0\),表示这件物品不再参与接下来的计算;而对区间最小值 \(minn\) 而言,为了保证当前产品的数量不会对祖先结点的取 \(\min\) 操作造成影响,则需要将其置为一个极大值。
上面这一步去除影响的操作是要递归到线段树的叶子结点的,但因为每件产品最多只会经历一次“不足 \(k_i\) 件但还没用完”的状态,也就是每个叶子结点最多只会被特殊修改一次,因此这里的时间复杂度仍然是 \(O(N\log N)\) 的。
时间复杂度 \(O((N+Q)\log N)\)。
代码
#define ls (p << 1)
#define rs (p << 1 | 1)
struct node
{
int l, r;
ll minn, cnt, lazy;
// 分别表示区间最小值、区间内未用完的产品个数、区间减少数量的 lazy 标记
} tr[300005 << 2];
int N;
ll A[300005]; // 初始数量
// 答案上传
void push_up(int p)
{
tr[p].minn = min(tr[ls].minn, tr[rs].minn); // 区间最小值
tr[p].cnt = tr[ls].cnt + tr[rs].cnt; // 未用完的产品数量 取总和
}
// 标记下传
void push_down(int p)
{
if(tr[p].lazy == 0)
return;
tr[ls].minn -= tr[p].lazy;
tr[ls].lazy += tr[p].lazy;
tr[rs].minn -= tr[p].lazy;
tr[rs].lazy += tr[p].lazy;
tr[p].lazy = 0;
}
// 建树
void build(int l, int r, int p = 1)
{
tr[p].l = l;
tr[p].r = r;
if(l == r)
{
tr[p].minn = A[l];
tr[p].cnt = 1;
return;
}
int mid = l + r >> 1;
build(l, mid, ls);
build(mid + 1, r, rs);
push_up(p);
}
// 查询答案
ll update_and_query(int l, int r, ll k, int p = 1)
{
// 区间内的产品均已用完
if(tr[p].cnt == 0)
return 0;
// 区间被问题完全包含,且每件物品都至少有 k 件
if(l <= tr[p].l && tr[p].r <= r && tr[p].minn > k)
{
tr[p].minn -= k;
tr[p].lazy += k;
return tr[p].cnt * k;
}
// 当前点是叶子结点,能运行到这里说明当前物品剩余数量不足 k 件
if(tr[p].l == tr[p].r)
{
ll res = tr[p].minn;
tr[p].cnt = 0;
tr[p].minn = 1e18; // 防止对还有库存的物品在取 min 时造成影响
return res;
}
push_down(p);
ll res = 0;
if(l <= tr[ls].r)
res += update_and_query(l, r, k, ls);
if(r >= tr[rs].l)
res += update_and_query(l, r, k, rs);
push_up(p);
return res;
}
void solve()
{
cin >> N;
for(int i = 1; i <= N; i++)
cin >> A[i];
build(1, N);
int Q;
cin >> Q;
while(Q--)
{
int l, r, k;
cin >> l >> r >> k;
cout << update_and_query(l, r, k) << "\n";
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号