AtCoder Beginner Contest 421 ABCDEF 题目解析
A - Misdelivery
题意
有 \(N\) 个房间,每个房间分别编号为 \(1,2, \dots, N\),第 \(i\) 个房间里住着一个名为 \(S_i\) 的人。
你现在要将一个包裹寄给 \(Y\) 先生/女士,包裹的目的地是 \(X\) 房间,请判断目的地是否正确(\(X\) 房间的住户是否名为 \(Y\))。
代码
#include<bits/stdc++.h>
using namespace std;
string s[105];
int main()
{
int n;
cin >> n;
for(int i = 1; i <= n; i++)
cin >> s[i];
int x;
string y;
cin >> x >> y;
if(s[x] == y)
cout << "Yes";
else
cout << "No";
return 0;
}
B - Fibonacci Reversed
题意
对于一个整数 \(x\),定义 \(f(x)\) 的值如下:
- 定义 \(s_x\) 表示将 \(x\) 在十进制表示下的字符串(不含前导零),定义 \(rev(s_x)\) 表示将 \(s_x\) 这个字符串前后翻转,则 \(f(x)\) 则表示将 \(rev(s_x)\) 当作一个十进制数字时的数值。
换言之,\(f(x)\) 表示把十进制数 \(x\) 前后倒转所得到的数。例如 \(f(13) = 31, f(10) = 01 = 1\)。
给定两个正整数 \(X, Y\),定义一个正整数序列 \(A = (A_1, A_2, \dots, A_{10})\) 如下:
- \(A_1 = X\)
- \(A_2 = Y\)
- \(A_i = f(A_{i-1} + A_{i-2})\) \((i \ge 3)\)
请输出 \(A_{10}\) 的值。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
// 将 n 进行首尾翻转
ll rev(ll n)
{
ll r = 0;
while(n > 0)
{
r = r * 10 + n % 10;
n /= 10;
}
return r;
}
ll a[11];
int main()
{
cin >> a[1] >> a[2];
for(int i = 3; i <= 10; i++)
a[i] = rev(a[i-1] + a[i-2]);
cout << a[10];
return 0;
}
C - Alternated
题意
给你一个长度为 \(2N\) 的字符串 \(S\) 。其中 \(S\) 恰好包含 \(N\) 个 A 和 \(N\) 个 B。
每次操作可以选择 \(S\) 中相邻的两个字符进行交换。
求使 \(S\) 中没有相邻的相同字符所需要的最少操作次数(可能为零)。
思路
由于题目保证 A 和 B 两种字符的出现次数相同,又因为最终要让所有相邻字符均不同,很明显操作完成后的字符串只有 ABABAB... 和 BABABA... 两种情况。
我们只需要分别求出交换成这两种情况分别所需要的最少操作次数,取个最小值就是最终答案。
(方法有很多种)以 ABABAB... 为例,我们可以只专注于考虑其中一种字符,比如 A 在字符串中出现的一定是奇数位置,如果我们能把所有 A 全部移动到奇数位置上,明显剩下的偶数位置肯定就全是 B 了。又因为交换两个相邻且相同的字符是没用的,所以我们可以遍历一遍整个字符串,从左往右遇到的每个字符 A 的目标位置一定是 \(1, 3, 5, 7, \dots\),直接统计每个字符 A 的当前位置与目标位置差值,累加即可。
时间复杂度 \(O(N)\)。
代码
#include<bits/stdc++.h>
using namespace std;
int n;
char s[1000005];
int main()
{
cin >> n;
cin >> (s + 1);
long long ab = 0, ba = 0; // ABAB... 与 BABA... 的答案
int cnta = 0, cntb = 0;
for(int i = 1; i <= 2 * n; i++)
{
if(s[i] == 'A')
{
cnta++;
// 第 cnta 个 A 移动到 2*cnta-1 位置上
ab += abs((2 * cnta - 1) - i);
}
else
{
cntb++;
// 第 cntb 个 B 移动到 2*cntb-1 位置上
ba += abs((2 * cntb - 1) - i);
}
}
cout << min(ab, ba) << "\n";
return 0;
}
D - RLE Moving
题意
有一张无限大的平面网格图,其中有个网格被称作坐标 \((0, 0)\) 处。从坐标 \((0, 0)\) 开始,往下 \(r\) 格再往右 \(c\) 格所到达的位置坐标可以描述为 \((r, c)\)。如果 \(r\) 是负数则说明往上,\(c\) 是负数则说明往左,具体如下图所示:
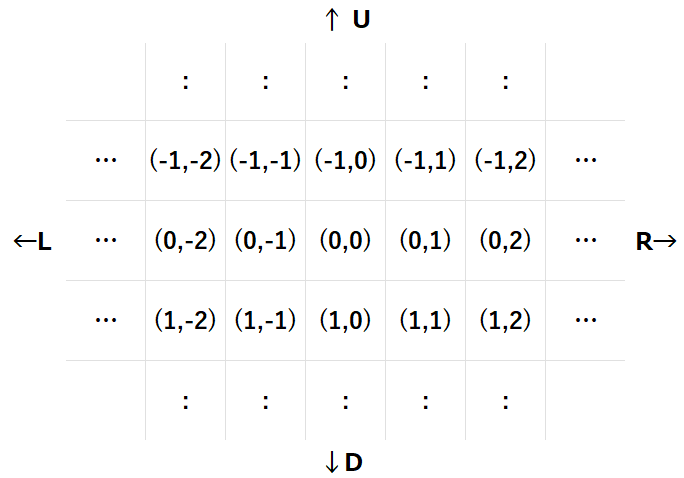
最初,高桥位于坐标 \((R_t,C_t)\) 处,青木位于坐标 \((R_a,C_a)\) 处。他们将分别根据长度为 \(N\) 的字符串 \(S\) 和 \(T\) 进行移动,字符串仅由 U、D、L、R 组成,分别表示向上、向下、向左、向右。
高桥和青木每一次都会同时移动。求在这 \(N\) 次移动当中,有多少次移动结束后,两人会走到相同格子上?
由于 \(N\) 非常大, \(S\) 和 \(T\) 以 \(((S'_1, A_1),\ldots,(S'_M,A_M))\) 和 \(((T'_1,B_1),\ldots,(T'_L,B_L))\) 这样的二元组形式给出。每个二元组包含一个整数与一个字符,其中 \((S_i', A_i)\) 表示连续出现了 \(A_i\) 次 \(S_i'\)。例如,\(((\texttt{U},3), (\texttt{L},2))\) 表示原字符串为 \(\texttt{UUULL}\)。
思路
总步数很大,肯定不能直接模拟,但因为 \(M, L \le 10^5\),也就是两人变向的次数不会超过 \(10^5\),所以我们可以采用双指针来解题,每次快速处理掉两人移动方向相同的一大段。
接下来便是分类讨论,假设现在高桥在 \((X_a, Y_a)\),方向为 \(Z_a\),简称其为 \(A\),青木在 \((X_b, Y_b)\),方向为 \(Z_b\),简称其为 \(B\),且接下来的 \(S\) 步两人的方向一直保持不变。
首先讨论两人的初始位置关系:
- 若两人初始位置完全相同 \((X_a=X_b,Y_a=Y_b)\)
- 接下来如果两人移动方向也相同 \((Z_a=Z_b)\),则每一步都是共点,答案 \(+S\)
- 接下来如果两人移动方向不同,接下来不可能再出现共点
- 若两人初始位置在同一行 \((X_a = X_b)\)
- 如果 \(A\) 在左,\(B\) 在右 \((X_a \lt X_b)\),且 \(A\) 朝右走,\(B\) 朝左走(相向而行),且两人之间的距离不超过 \(2S\)(否则走不到共点的位置),且两人之间的距离是个偶数(不然可能会在最后一步错过)时,答案 \(+1\)
- \(A, B\) 交换亦然
- 若两人初始位置在同一列 \((Y_a = Y_b)\)
- 如果 \(A\) 在上,\(B\) 在下 \((Y_a \lt Y_b)\),且 \(A\) 朝下走,\(B\) 朝上走(相向而行),且两人之间的距离不超过 \(2S\)(否则走不到共点的位置),且两人之间的距离是个偶数(不然可能会在最后一步错过)时,答案 \(+1\)
- \(A, B\) 交换亦然
- 除以上三种情况以外 \((X_a \ne X_b, Y_a \ne Y_b)\)
- 此时只有当两个人在某个正方形的两条相邻边上走时才有可能相遇,即初始位置是某个正方形对角线的点,且两人移动方向不平行,且总步数不少于正方形边长 \((|X_a - X_b| = |Y_a - Y_b| \le S)\)
- 以 \(A\) 在 \(B\) 的左上角为例,此时 \(A\) 朝右走,\(B\) 朝上走可以碰到一起,或者 \(A\) 朝下走,\(B\) 朝左走也能碰到一起
- 剩余四种情况类似,详见代码
时间复杂度 \(O(M+L)\)。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll xa, ya, xb, yb; // 两人当前位置
ll n; // 总步数
int m, l;
char s[100005], t[100005];
ll a[100005], b[100005];
// a[i], b[i] 处理前缀和
// 分别表示两人 第 i 个方向走到哪一步结束
ll ans = 0; // 两人相遇次数
// 处理两人分别从 (xa, ya) (xb, yb) 出发
// 第一个人一直往 a 方向走,第二个人往 b 方向走
// step 步以内的相遇次数
void move(char a, char b, ll step)
{
if(xa == xb && ya == yb) // 初始位置和方向均相同时,每一步都会相遇
{
if(a == b)
ans += step;
}
else if(xa == xb) // 行相同或列相同时,相向而行可能相遇一次
{
if(a == 'R' && b == 'L' && ya < yb && yb - ya <= step * 2 && (yb - ya) % 2 == 0)
ans++;
if(b == 'R' && a == 'L' && yb < ya && ya - yb <= step * 2 && (ya - yb) % 2 == 0)
ans++;
}
else if(ya == yb)
{
if(a == 'D' && b == 'U' && xa < xb && xb - xa <= step * 2 && (xb - xa) % 2 == 0)
ans++;
if(b == 'D' && a == 'U' && xb < xa && xa - xb <= step * 2 && (xa - xb) % 2 == 0)
ans++;
}
else // 行列均不同时
{
// 只有当两人行列差值相同,才有可能相遇一次
if(abs(xb - xa) == abs(yb - ya) && abs(xb - xa) <= step)
{
if(xa < xb && ya < yb) // 此时 a 在 b 的左上
{
if(a == 'R' && b == 'U')
ans++;
if(a == 'D' && b == 'L')
ans++;
}
else if(xa > xb && ya < yb) // 此时 a 在 b 的左下
{
if(a == 'R' && b == 'D')
ans++;
if(a == 'U' && b == 'L')
ans++;
}
else if(xa < xb && ya > yb) // 此时 a 在 b 的右上
{
if(a == 'D' && b == 'R')
ans++;
if(a == 'L' && b == 'U')
ans++;
}
else // 此时 a 在 b 的右下
{
if(a == 'U' && b == 'R')
ans++;
if(a == 'L' && b == 'D')
ans++;
}
}
}
if(a == 'U') xa -= step;
else if(a == 'D') xa += step;
else if(a == 'L') ya -= step;
else if(a == 'R') ya += step;
if(b == 'U') xb -= step;
else if(b == 'D') xb += step;
else if(b == 'L') yb -= step;
else if(b == 'R') yb += step;
}
int main()
{
cin >> xa >> ya >> xb >> yb;
cin >> n >> m >> l;
for(int i = 1; i <= m; i++)
{
cin >> s[i] >> a[i];
a[i] += a[i-1]; // 处理步数前缀和
}
for(int i = 1; i <= l; i++)
{
cin >> t[i] >> b[i];
b[i] += b[i-1];
}
int i = 1, j = 1; // 两人分别处理到了哪一段
ll sum = 0; // 目前已经处理的总步数
while(sum < n)
{
ll step = min(a[i], b[j]) - sum; // 这一次要处理的总步数
move(s[i], t[j], step); // 这 step 步以内两人的方向是不变的
sum += step;
if(a[i] == sum)
i++;
if(b[j] == sum)
j++;
}
cout << ans;
return 0;
}
E - Yacht
题意
有五个相同的六面骰子。骰子的每个面上都写着数字 \(A_1,\ldots,A_6\) ,每个面出现的概率均为 \(\frac{1}{6}\) 。
你将用这些骰子玩一个单人游戏,游戏流程如下:
- 掷出所有五颗骰子,观察结果,并保留任意数量(可能是零)的骰子。
- 重新掷出所有未保留的骰子,观察结果,并保留任意数量(可以为零)的重新掷出的骰子。上一步保留的骰子继续保留。
- 同 2,重掷所有未保留的骰子,观察结果。
- 选择任意一个数字 \(X\) 。记 \(n\) 为最终的五个骰子中以 \(X\) 朝上的骰子的数量。游戏的得分即 \(nX\) 点。
请求出游戏分数的最大期望值。
思路
考虑期望DP,记 dp[i][j][k] 表示剩余投掷次数为 \(i\) 次,已保留的骰子数量为 \(j\) 个,且已保留的骰子点数集合为 \(k\) 时所能获得的最大期望值。这里的 \(k\) 描述为由 \(5\) 个 \(0\sim 5\) 之间的数组成的六进制数值,表示保留下来的每个骰子朝上的点数是 \(A\) 数组中的哪个下标代表的数。(输入时把 \(A\) 数组下标也替换为 \(0\sim 5\))
已知在投掷完三次之后,五个骰子的情况一定是确定的,因此我们可以预处理出投掷三次后的每一种骰子点数集合 \(k\),获得 dp[0][5][k] 的初始值。
接下来考虑状态转移。对于 dp[i][j][k] 而言,还有 \(5-j\) 颗骰子没有投出,因此我们需要先把 \(6^{5-j}\) 种未保留的骰子的投掷情况枚举出来,然后再枚举 \(2^{5-j}\) 种保留情况,根据保留情况处理出保留下来的集合,记作 \(u\),本次保留的骰子数量记作 \(cnt\)。明显集合 \(k\) 与集合 \(u\) 满足 \(k \subset u\)。那么在当前保留情况下所能获得的最大期望值便可以通过 dp[i-1][j+cnt][u] 得到。对于每一种投掷情况,我们都可以在所有保留情况当中取一个最大期望值作为我们实际选择的保留集合,投掷情况出现的概率均为 \(\frac{1}{6^{5-j}}\),将概率与最大期望值相乘,加入到 dp[i][j][k] 中即可。
时间复杂度 \(O(TNM^N2^N)\),其中 \(T=3\) 表示投掷次数,\(N=5\) 表示骰子数量,\(M = 6\) 表示骰子面数。
代码
#include<bits/stdc++.h>
using namespace std;
int a[6];
int pw6[6];
// pw6[i] 表示 6 的 i 次方
double dp[4][6][7776];
// dp[i][j][k] 表示剩余投掷次数为 i 次
// 已保留的骰子数量为 j 个
// 已保留的点数(下标)集合为 k 时的期望最大值(哈希为 5 位 0~5 的数字)
int main()
{
for(int i = 0; i < 6; i++)
cin >> a[i];
pw6[0] = 1;
for(int i = 1; i <= 5; i++)
pw6[i] = pw6[i - 1] * 6;
for(int i = 0; i <= 4; i++)
for(int j = 0; j < pw6[i]; j++)
dp[0][i][j] = -1e18;
for(int i = 0; i < pw6[5]; i++)
{
int msk = i;
int cnt[6] = {0, 0, 0, 0, 0, 0}; // 每一面出现的次数
for(int j = 1; j <= 5; j++)
{
cnt[msk % 6]++;
msk /= 6;
}
int mx = 0;
for(int j = 0; j < 6; j++)
{
int num = 0; // 如果选择 a[j] 作为最终值,统计 a[j] 出现次数
for(int k = 0; k < 6; k++)
if(a[k] == a[j]) // k 下标与 j 下标的值相同,也可以当作是投出了 a[j]
num += cnt[k];
mx = max(mx, num * a[j]); // 以 a[j] 作为最终值的期望,取最大值
}
dp[0][5][i] = mx;
}
for(int t = 1; t <= 3; t++) // 剩余投掷次数
{
for(int keep = 0; keep <= 5; keep++) // 已保留的骰子个数
{
for(int msk = 0; msk < pw6[keep]; msk++) // 已保留的点数集合
{
for(int msknow = 0; msknow < pw6[5 - keep]; msknow++) // 新投掷的点数集合
{
double mx = 0; // 在本次所有投掷情况中
for(int choose = 0; choose < (1 << (5 - keep)); choose++) // 枚举新投掷的集合需要保留的二进制状态
{
int store = msk; // 存储新的要保留的点数集合
int tmp = msknow;
for(int k = 0; k < 5 - keep; k++)
{
if(choose >> k & 1) // 如果当前这一位所表示的骰子是需要保留的
store = store * 6 + tmp % 6;
tmp /= 6;
}
int cnt = __builtin_popcount(choose); // 新增要保留的数字数量
mx = max(mx, dp[t - 1][keep + cnt][store]);
}
dp[t][keep][msk] += mx / pw6[5 - keep]; // 在所有可能的保留情况当中取一个最大期望保留,期望值乘上本次投掷出的点数集合概率
}
}
}
}
cout << fixed << setprecision(10) << dp[3][0][0];
return 0;
}
F - Erase between X and Y
题意
有一个序列 \(A\) 。初始为 \(A=(0)\) 。(也就是说,\(A\) 是一个长度为 \(1\) 的序列,其中唯一的元素是 \(0\) )。
您需要依次处理 \(Q\) 个查询。第 \(i\) 次查询 \((1\leq i\leq Q)\) 为以下两种形式之一:
-
1 x:在 \(A\) 中 \(x\) 所出现的位置之后紧接着插入数字 \(i\) 。- 换句话说,当 \(p\) 满足 \(A_p=x\) 时,将 \(A\) 更新为 \((A_1,\dots,A_p,i,A_{p+1},\dots,A_n)\) 。保证在处理此次查询之前,\(A\) 中已经包含 \(x\)。
-
2 x y:删除 \(A\) 中介于 \(x\) 和 \(y\) 之间的所有元素,并输出被删除的元素之和。- 换句话说,当 \(p\) 和 \(q\) 满足 \(A_p=x\) 且 \(A_q=y\) 时,请输出 \(A_{\min(p,q)+1} + \dots + A_{\max(p,q)-1}\) 的值,并将 \(A\) 更新为 \((A_1,\dots,A_{\min(p,q)},A_{\max(p,q)},\dots,A_n)\) 。保证在处理此次查询之前,\(A\) 中已经包含 \(x\) 和 \(y\)。
思路
明显除了 \(0\) 以外的每个数字只会被插入一次,且最多被查询并删除一次,所以我们可以采用链表来维护这个序列。
插入操作比较方便,重点是查询及删除操作,我们无法通过两个链表结点的值 \(x, y\) 来直接判断这两个结点谁在前谁在后。
这里有一个技巧,我们可以尝试在链表上暴力往后跳,但是 \(x\) 和 \(y\) 需要同时跳。这样最终出现的情况无非就两种:靠前的结点碰到靠后的结点,或者靠后的结点碰到链表尾。
- 如果是靠前的结点先碰到靠后的结点,我们便可以直接判断 \(x, y\) 在原链表内的先后顺序,并且这一次跳跃的总次数近乎等同于我们要删除的结点总数。
- 如果是靠后的结点先碰到链表尾,我们也同样可以判断 \(x, y\) 在原链表内的先后顺序,并且这一次跳跃的总次数小于我们要删除的结点总数。
综上,暴力向后跳的时间复杂度可以近似等同于要删除的结点数量,链表模拟的时间复杂度是 \(O(N)\) 的。
代码
#include<bits/stdc++.h>
using namespace std;
int pre[500005];
int nxt[500005];
// 维护双向链表前后两个结点
int main()
{
pre[0] = nxt[0] = -1;
int q;
cin >> q;
for(int i = 1; i <= q; i++)
{
int op;
cin >> op;
if(op == 1)
{
int x, y;
cin >> x;
if(nxt[x] != -1) // x 不是链表的最后一个元素
{
y = nxt[x]; // 在 x 和 y 之间插入一个 i
nxt[x] = pre[y] = i;
}
else // x 是链表的最后一个元素
{
y = -1;
nxt[x] = i;
}
pre[i] = x;
nxt[i] = y;
}
else
{
int x, y;
cin >> x >> y;
// 暴力向后跳
int tx = x, ty = y;
while(true)
{
if(tx == y || ty == -1) // 说明 x 在 y 前
break;
if(ty == x || tx == -1) // 说明 y 在 x 前
{
swap(x, y);
break;
}
tx = nxt[tx];
ty = nxt[ty];
}
// 此时 x 在前 y 在后
long long sum = 0;
tx = x;
while(true)
{
tx = nxt[tx];
if(tx == y)
break;
sum += tx;
}
cout << sum << "\n";
// 从链表内删除 nxt[x] ~ pre[y]
nxt[x] = y;
pre[y] = x;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号