Codeforces Round #719 (Div. 3) 解题思路
Codeforces Round #719 (Div. 3)
A - Do Not Be Distracted!
题意
给定长度为\(n\)的仅包含大写字母的字符串\(S\)
问相同的字符是否只连续出现了一段
思路
直接遍历,每找到一段就标记一次,检查当前段是否已经被标记过即可
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define all(a) (a).begin(),(a).end()
#define mst(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define eb emplace_back
using namespace std;
//using namespace __gnu_pbds;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const ll mod=998244353;
mt19937 mt19937random(std::chrono::system_clock::now().time_since_epoch().count());
ll getRandom(ll l,ll r){return uniform_int_distribution<ll>(l,r)(mt19937random);}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}
void solve()
{
int n;
string s;
cin>>n>>s;
int v[26]={0};
repp(i,0,n)
{
char c=s[i];
if(!v[c-'A'])
{
v[c-'A']=1;
int j=i;
while(j<n&&s[j]==s[i])
j++;
i=j-1;
}
else
{
cout<<"NO\n";
return;
}
}
cout<<"YES\n";
}
int main()
{
closeSync;
multiCase
{
solve();
}
return 0;
}
B - Ordinary Numbers
题意
定义一个数字是ordinary的,当且仅当它每一位上的数字都相同
问\(1\)到\(n\)中有多少个数字是ordinary的
思路
\(10^9\)的范围内仅存在\(9*9=81\)个合法数字,直接预处理后二分即可
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define all(a) (a).begin(),(a).end()
#define mst(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define eb emplace_back
using namespace std;
//using namespace __gnu_pbds;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const ll mod=998244353;
mt19937 mt19937random(std::chrono::system_clock::now().time_since_epoch().count());
ll getRandom(ll l,ll r){return uniform_int_distribution<ll>(l,r)(mt19937random);}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}
vector<ll> vec;
void init()
{
rep(i,1,9) //枚举数字
{
ll v=0;
rep(j,1,9) //枚举位数
{
v=v*10+i;
vec.pb(v);
}
}
sort(all(vec));
}
void solve()
{
int n;
cin>>n;
cout<<(upper_bound(all(vec),n)-vec.begin())<<'\n';
}
int main()
{
closeSync;
init();
multiCase
{
solve();
}
return 0;
}
C - Not Adjacent Matrix
题意
构造一个\(n\times n\)的矩阵,使得相邻两个数的差值\(\gt 1\),且\(1\)到\(n^2\)内每个数都在矩阵中出现一次
思路
仅在\(n=2\)时不存在解
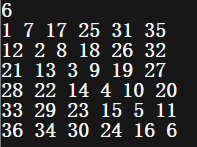
其余情况,可以都沿着主对角线方向按顺序放置
主要思路可看下图,按数字顺序放置
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define all(a) (a).begin(),(a).end()
#define mst(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define eb emplace_back
using namespace std;
//using namespace __gnu_pbds;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const ll mod=998244353;
mt19937 mt19937random(std::chrono::system_clock::now().time_since_epoch().count());
ll getRandom(ll l,ll r){return uniform_int_distribution<ll>(l,r)(mt19937random);}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}
int a[105][105];
void solve()
{
int n;
cin>>n;
if(n==1)
{
a[1][1]=1;
}
else if(n==2)
{
cout<<"-1\n";
return;
}
else
{
int cur=0;
rep(i,1,n) //主对角线
a[i][i]=++cur;
rep(i,2,n)
{
for(int x=1,y=i;y<=n;x++,y++) //主对角线右上方
a[x][y]=++cur;
for(int x=i,y=1;x<=n;x++,y++) //主对角线左下方
a[x][y]=++cur;
}
}
rep(i,1,n)
rep(j,1,n)
cout<<a[i][j]<<(j==n?'\n':' ');
}
int main()
{
closeSync;
multiCase
{
solve();
}
return 0;
}
D - Same Differences
题意
给定一个数列\(\{a\}\)
询问存在多少二元组\((i,j)\),满足\(i\lt j\)且\(a_j-a_i=j-i\)
思路
\(a_j-a_i=j-i\)看作\(a_j-j=a_i-i\)
按顺序遍历每个位置的数
map存储出现的\(a_j-j\)的次数作为当前位置\(j\)所匹配上的\(i\)的数量即可
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define all(a) (a).begin(),(a).end()
#define mst(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define eb emplace_back
using namespace std;
//using namespace __gnu_pbds;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const ll mod=998244353;
mt19937 mt19937random(std::chrono::system_clock::now().time_since_epoch().count());
ll getRandom(ll l,ll r){return uniform_int_distribution<ll>(l,r)(mt19937random);}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}
int a[200050];
void solve()
{
map<int,int> mp;
int n;
cin>>n;
ll ans=0;
rep(i,1,n)
{
cin>>a[i];
ans+=mp[a[i]-i];
mp[a[i]-i]++;
}
cout<<ans<<'\n';
}
int main()
{
closeSync;
multiCase
{
solve();
}
return 0;
}
E - Arranging The Sheep
题意
给定一个字符串\(S\),仅包含字符\(.\)与\(*\)分别表示空地和绵羊
每次操作可以将任意一只绵羊往左或者往右移动一格,只要目标位置存在且为空地
要求将所有绵羊弄到一起(任意两只绵羊间不能有空地)
问最小的操作数
思路
令\(suml[i]\)表示将初始状态的\(i\)点左侧的所有绵羊全部向右移动到\(i\)点(且往左排列)所需要的最小操作数
同理,\(sumr[i]\)表示将初始状态的\(i\)点右侧的所有绵羊全部向左移动到\(i\)点(且往右排列)所需要的最小操作数
以预处理\(suml\)为例,从左向右遍历字符串\(S\)
-
如果位置\(i\)是空地,那么将左侧所有羊全部移动到\(i\)点(且往左排列)的操作数,就是将左侧所有羊全部移动到\(i-1\)点(且往左排列)后,再依次将\(cntl[i]\)只羊向右移动一格到\(i\)点(且往左排列),故\(suml[i]=suml[i-1]+cntl[i]\),\(cntl[i]\)表示初始状态下\(i\)点左侧的绵羊数量
-
如果位置\(i\)是绵羊,如果此前已经将\(i-1\)点左侧所有羊全部移动到\(i-1\)点(且往左排列)了的话,这一步转移就不需要进行移动,即\(suml[i]=suml[i-1]\),注意此时\(cntl[i]=cntl[i-1]+1\)
预处理\(sumr\)同理,从右向左遍历即可
最后,枚举\(1\)到\(n\)所有位置\(p\),表示将\(p\)点左右两侧所有羊都移动到\(p\)点(向左右排列),直接维护答案取最小值即可
\(ans=min\{suml[p-1]+sumr[p+1]+t\}\)
\(t\)表示如果\(p\)点刚开始不是只羊的话,还需要将某一侧的羊再依次移动一格,即\(t=min(cntl[i],cntr[i])\)
如果\(p\)点刚开始已经是只羊,\(t=0\)
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define all(a) (a).begin(),(a).end()
#define mst(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define eb emplace_back
using namespace std;
//using namespace __gnu_pbds;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const ll mod=998244353;
mt19937 mt19937random(std::chrono::system_clock::now().time_since_epoch().count());
ll getRandom(ll l,ll r){return uniform_int_distribution<ll>(l,r)(mt19937random);}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}
char s[1000050];
ll cntl[1000050],cntr[1000050];
ll suml[1000050],sumr[1000050];
void solve()
{
int n;
cin>>n>>s+1;
cntl[0]=0;
suml[0]=0;
rep(i,1,n)
{
if(s[i]=='*')
{
cntl[i]=cntl[i-1]+1;
suml[i]=suml[i-1];
}
else
{
cntl[i]=cntl[i-1];
suml[i]=suml[i-1]+cntl[i];
}
}
cntr[n+1]=0;
sumr[n+1]=0;
per(i,n,1)
{
if(s[i]=='*')
{
cntr[i]=cntr[i+1]+1;
sumr[i]=sumr[i+1];
}
else
{
cntr[i]=cntr[i+1];
sumr[i]=sumr[i+1]+cntr[i];
}
}
ll ans=LINF;
rep(i,1,n)
{
ll ansd=suml[i-1]+sumr[i+1];
if(s[i]=='.')
ansd+=min(cntl[i],cntr[i]);
ans=min(ans,ansd);
}
cout<<ans<<'\n';
}
int main()
{
closeSync;
multiCase
{
solve();
}
return 0;
}
F1 - Guess the K-th Zero (Easy version)
题意
现有一个长度为\(n\le 2\cdot 10^5\)的\(01\)序列,\(t=1\)
每次你可以输出\(?\ l\ r\)来查询\([l,r]\)的区间和,最多查询\(20\)次
要求你找到第\(k\)个\(0\)的下标是多少(从\(1\)开始)
思路
直接二分即可,维护一个可行区间\([l,r]\),初始\(l=1,r=n\)
每次查询\([l,mid]\),区间长度为\(mid-l+1\),查询的返回值\(res\)即代表着区间中\(1\)的个数
则\(mid-l+1-res\)即区间内\(0\)的个数
如果\(mid-l+1-res\lt k\),即区间内\(0\)的个数小于待查找的\(0\)的位置,此时将\(l=mid+1\)来缩小维护的可行区间,且让\(k-=mid-l+1-res\),表示在当前维护的区间中我们只需要找到第\(k-(mid-l+1-res)\)个\(0\)的下标即可
如果\(mid-l+1-res\ge k\),则表示第\(k\)个\(0\)在查询的\([l,mid]\)区间内,此时让\(r=mid\)即可
直到\(l==r\),输出即可,查询次数为\(\log n\le 20\)
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define all(a) (a).begin(),(a).end()
#define mst(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define eb emplace_back
using namespace std;
//using namespace __gnu_pbds;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const ll mod=998244353;
mt19937 mt19937random(std::chrono::system_clock::now().time_since_epoch().count());
ll getRandom(ll l,ll r){return uniform_int_distribution<ll>(l,r)(mt19937random);}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}
int main()
{
int n,t,k;
scanf("%d%d%d",&n,&t,&k);
int T=20;
int l=1,r=n;
while(T--)
{
int m=(l+r)>>1;
int len=m-l+1;
printf("? %d %d\n",l,m);
fflush(stdout);
int res;
scanf("%d",&res);
int cnt=len-res;
if(cnt<k)
{
k-=cnt;
l=m+1;
}
else
r=m;
if(l==r)
{
printf("! %d\n",l);
break;
}
}
return 0;
}
F2 - Guess the K-th Zero (Hard version)
题意
思路
不会了明天补……
G - To Go Or Not To Go?
题意
给定一张\(n\times m\)的图,起点为\((1,1)\),终点为\((n,m)\)
每个点都有一个值,\(-1\)表示不可走,\(0\)表示可走,其余值表示可走且存在一个花费为\(a_{i,j}\)的传送器
行走只能向上下左右四个方向走,每走一步花费为\(w\)
使用传送器可以立即传送到任意一个其它传送器的位置上,花费为两个传送器的\(a_{i,j}\)之和
问从起点走到终点的最小花费,不存在输出\(-1\)
思路
从起点搜一次到每个可走到的点的最短距离存在\(dis1\)中
从终点搜一次到每个可走到的点的最短距离存在\(dis2\)中
由于可以任意传送,所以如果使用传送器的话肯定只使用一次
所以\(dis1[i][j]+a[i][j]\)就可以表示从起点走到\((i,j)\)并使用了这个传送器的花费(如果存在传送器)
同理\(dis2[i][j]+a[i][j]\)就可以表示从\((i,j)\)走到终点并使用了这个传送器的花费(如果存在传送器)
维护上面两个的最小值,相加后再与不使用任何传送器的情况(即\(dis1[n][m]\)或\(dis2[1][1]\))取小输出即可
注意不存在的情况输出\(-1\)
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define all(a) (a).begin(),(a).end()
#define mst(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define eb emplace_back
using namespace std;
//using namespace __gnu_pbds;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const ll mod=998244353;
mt19937 mt19937random(std::chrono::system_clock::now().time_since_epoch().count());
ll getRandom(ll l,ll r){return uniform_int_distribution<ll>(l,r)(mt19937random);}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int n,m,w;
int mp[2050][2050];
vector<P> vec;
ll dis1[2050][2050],dis2[2050][2050];
inline bool prim(int x,int y)
{
return x>0&&y>0&&x<=n&&y<=m;
}
void bfs(int stx,int sty,ll dis[2050][2050])
{
rep(i,1,n)
rep(j,1,m)
dis[i][j]=LINF;
dis[stx][sty]=0;
queue<P> q;
q.push(P(stx,sty));
while(!q.empty())
{
P pd=q.front();
q.pop();
int &x=pd.first,&y=pd.second;
rep(i,0,3)
{
int px=dx[i]+x,py=dy[i]+y;
if(prim(px,py)&&mp[px][py]!=-1&&dis[px][py]>dis[x][y]+w)
{
dis[px][py]=dis[x][y]+w;
q.push(P(px,py));
}
}
}
}
void solve()
{
cin>>n>>m>>w;
rep(i,1,n)
rep(j,1,m)
cin>>mp[i][j];
bfs(1,1,dis1);
bfs(n,m,dis2);
ll tmp1=LINF,tmp2=LINF;
rep(i,1,n)
rep(j,1,m)
{
if(mp[i][j]<=0)
continue;
tmp1=min(tmp1,dis1[i][j]+mp[i][j]);
tmp2=min(tmp2,dis2[i][j]+mp[i][j]);
}
ll ans=min(tmp1+tmp2,dis1[n][m]);
if(ans>=LINF)
ans=-1;
cout<<ans<<'\n';
}
int main()
{
closeSync;
//multiCase
{
solve();
}
return 0;
}
https://blog.csdn.net/qq_36394234/article/details/116433136


 浙公网安备 33010602011771号
浙公网安备 33010602011771号