AtCoder Contest 188题解 (已补完)

目录

• A - Three-Point Shot
• B - Orthogonality
• C - ABC Tournament
• D - Snuke Prime
• E - Peddler
• F - +1-1x2

A - Three-Point Shot

签

B - Orthogonality

签

C - ABC Tournament

题意：

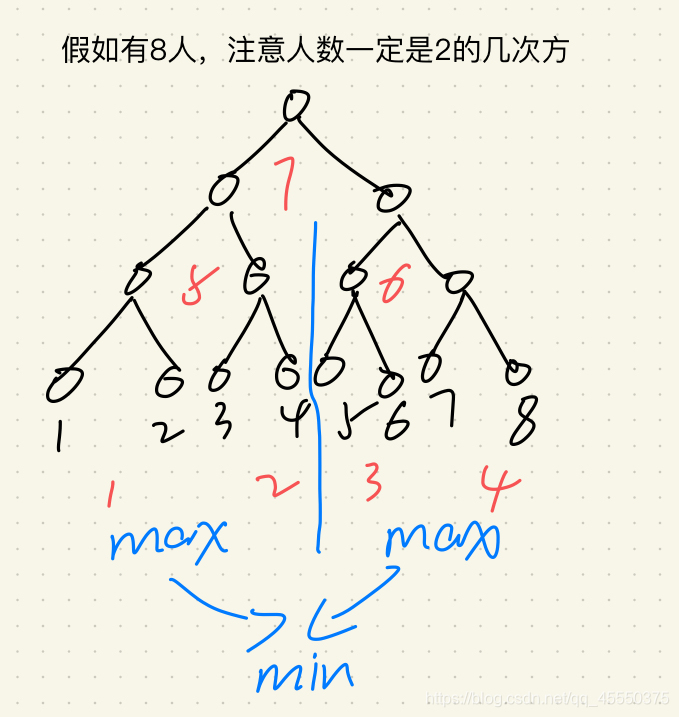
给你\(2^n\)个数，每轮相邻两位pk，分数高的获胜，进入下一轮，求最后进入决赛被淘汰的人的位置

思路：

#include<bits/stdc++.h>
using namespace std;
template<class T>inline void read(T &x){
    x=0;register char c=getchar();register bool f=0;
    while(!isdigit(c))f^=c=='-',c=getchar();
    while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
    if(f)x=-x;
}
int main(){
	int n,t;
	cin>>n;
	int min1=-INT_MAX,min2=-INT_MAX;
	int ans1=0,ans2=0;
	int l=pow(2,n)/2,r=pow(2,n);
	for(int i=1;i<=l;i++){
		read(t);
		if(min1<t)
			ans1=i,min1=t;		
	}
	for(int i=l+1;i<=r;i++){
		read(t);
		if(min2<t)
			ans2=i,min2=t;
	}
	if(min1>min2)cout<<ans2<<endl;
	else cout<<ans1<<endl;
}

D - Snuke Prime

思路：

离散化 + 差分，判断一段区间的值如果比\(C\)大，那么这段区间价钱用\(C\)替代，反之不替代

复习stl：STL总结(14种)

#include<bits/stdc++.h>
#define LL long long
#define mem(f, x) memset(f,x,sizeof(f)) 
#define Sca(x) scanf("%d", &x)
#define Sca2(x,y) scanf("%d%d",&x,&y)
#define fo(i,a,n) for(int i=a;i<=n;++i)
using namespace std;
template<class T>inline void read(T &x){
    x=0;register char c=getchar();register bool f=0;
    while(!isdigit(c))f^=c=='-',c=getchar();
    while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
    if(f)x=-x;
}
map<LL, LL> m;//离散化 
int main(){
	LL n,c;
	cin>>n>>c;
	LL t,t1,t2;
	for(int i=0;i<n;i++){
		read(t1);read(t2);read(t);
		//构造离散差分数组
		m[t1]+=t;
		m[t2+1]-=t;
	}
	LL s=(*m.begin()).first,k=(*m.begin()).second;
	LL p,q;
	LL sum=0;
	map<LL, LL>::iterator it=m.begin(); 
	for(it++;it!=m.end();it++){
		p=(*it).first,q=(*it).second; 
		
		if(k>c)sum+=c*(p-s);		
		else sum+=(k)*(p-s);
		
		k+=q;//求差分
		s=p;
	}
	cout<<sum;
	return 0;
}

E - Peddler

题意：

n点m边的有向图，点权代表黄金价格，其中边\(<x,y>\)满足\(x_{i}\)一定小于\(y_{i}\)
现在他要选一个点买黄金，然后走到另外一个点卖黄金，求最大利润。

思路：

跑一个dfs，f[i]表示从第i个点走到最后黄金的最大价格，然后更新f[i] - a[i]最大值

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 10;
int a[N];
int f[N];//f[i]表示从第i个点走到最后黄金的最大价格 
vector<int> g[N];//邻接表 
bool st[N];
int n,m;
template<class T>inline void read(T &x){
    x=0;register char c=getchar();register bool f=0;
    while(!isdigit(c))f^=c=='-',c=getchar();
    while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
    if(f)x=-x;
}
void dfs(int u){
    st[u] = true;
    for(auto t:g[u]){
        if(!st[t]) dfs(t);
        //f[i]表示从第i个点走到最后黄金的最大价格
        f[u] = max(f[u],max(f[t],a[t]));//更新讨论各种情况 
    }
}
int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++) read(a[i]);
    while(m--){
        int x,y;
        read(x);read(y);
        g[x].push_back(y);
    }
    memset(f,-0x3f,sizeof f);
    for(int i = 1;i <= n;i++)
        if(!st[i])dfs(i);
    int ans = -INF;
    for(int i = 1;i <= n;i++) 
		ans = max(f[i] - a[i],ans);//更新f[i]-a[i]的最大值
    printf("%d",ans);
    return 0;
}

F - +1-1x2

思路：

记忆化dp裸题，类似滑雪
dp[y]和dfs(y)都表示将x变成y需要的步数

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 2e5 + 5;
template<class T>inline void read(T &x){
    x=0;register char c=getchar();register bool f=0;
    while(!isdigit(c))f^=c=='-',c=getchar();
    while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
    if(f)x=-x;
}
//记忆化dp裸题
map<ll, ll> dp;
ll x, y;
ll dfs(ll yy){
    if(yy <= x) return x - yy;//x只能进行x-yy次 减操作到达yy
    if(dp.count(y)) return dp[yy];//记忆化操作直接返回
    ll res = yy - x;
    if(yy % 2 == 0) res = min(res, dfs(yy / 2) + 1);//如果yy是偶数，那么就存在乘2的操作，使得x到达yy
    else res = min(res, 1 + min(dfs(yy + 1), dfs(yy - 1))); //不然就看看加1减1操作使得x到达yy，取一个最小值
    return dp[yy] = res;
}
int main(){
    read(x);read(y);
    cout << dfs(y);
    return 0;
}