学习数据结构的第十天（三）（包括以后一些学习的指引）

对于递归的 时间复杂度的计算，其实我不太会去计算的，像这里如果说用递归去实现find的话，就是优化后的find，时间复杂度为什么接近O1呢？

并查集的能否直接用接口使用呢？什么情况 ，实战案例用了并查集呢

并查集目的：

并是什么意思，并是合并的意思，查是什么意思，查是查阅的意思。

并查集含义：合并   查阅。

将两个小集合合并，或者查询两个元素是否属于同一个集合，就是并查集。

(其实查询的话，觉得最小的情况，不就是logN吗，如果说是二分搜索树进行查找。)

也就是知道并查集的目的，如果涉及到两个集合的合并以及查找某个集合里面是否有某个元素就是并查集。

key：这里说的是并查集的目的。

这里说的是并查集的一种实现，是归类法。  

即拿某个数组来实现，对于数组里面的每个元素，就代表了这个元素属于哪个集合这个要点。

 

 

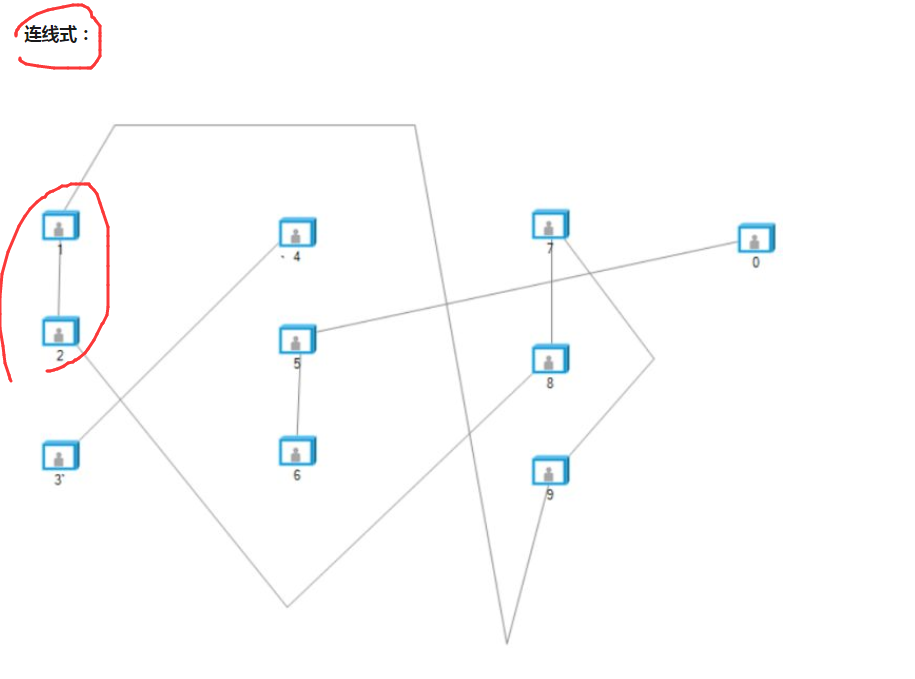
 连线式说的是   某个元素指向另外一个元素，指向的元素是属于同一个集合的。

 

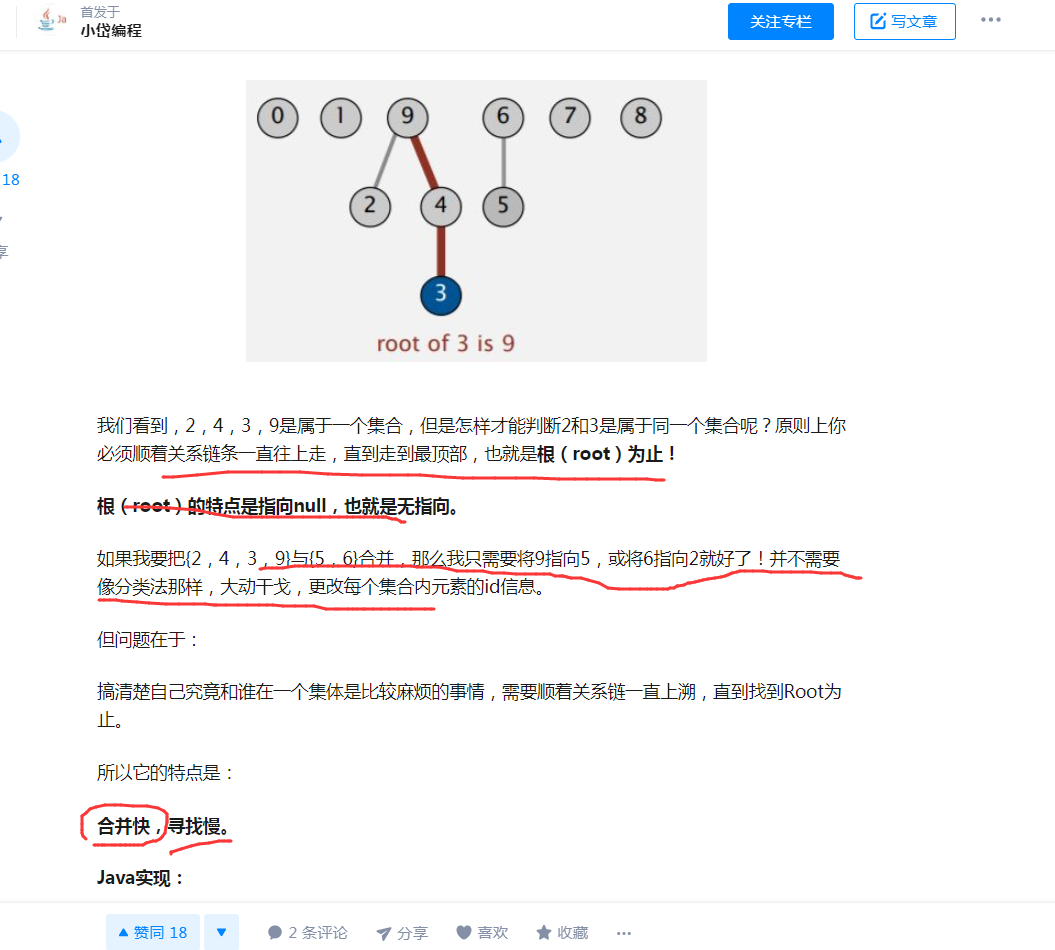
 然后这里说的是连线式的优点，合并快，查找慢。

 

 对于代码而言

 

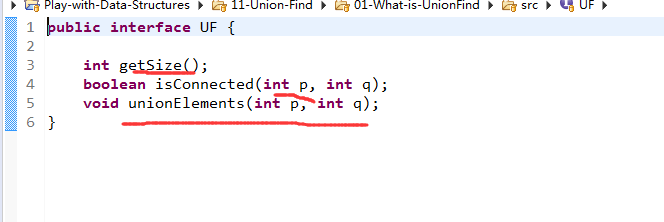
 就是（1）返回元素的代码（2）判断两个元素是不是相连结的代码  

（3）合并两个元素所在的集合

 

这里讲的是：并查集这个接口的方法都是什么

 

 

 

 

 

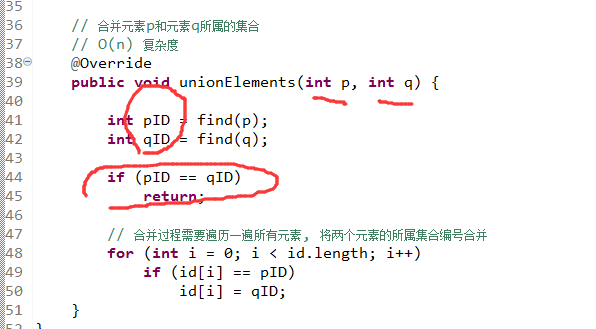
这个是：归类法来实现的union find

确实可以看出来，查找是O（1）  然后的话合并是O（N）

 

 

 

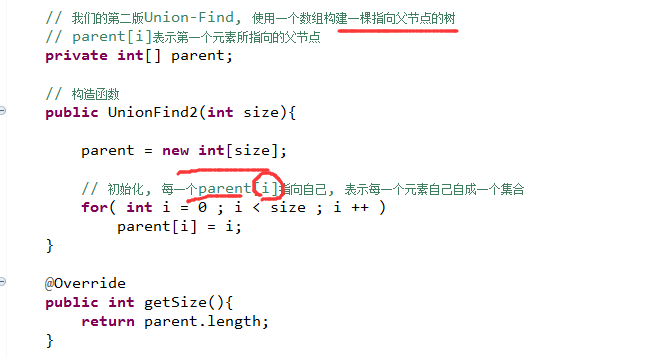
 这是第二种方法，i对应的parent i   表示的是i元素的父节点是什么。

 

 这里说的是查找这个元素属于什么集合的操作

key：i元素的parent【i】的值，意思是：  它的父节点的值是什么

时间复杂度确实是O（h）

并不是说O（n）

如果说你这些元素都处于同一个集合，并且是链状的指向，那么确实退化成了O（n）

 

 

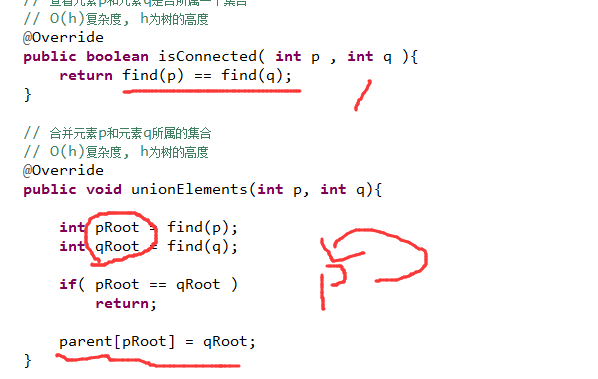
 这里说的是  如果说用这个  连线法

那么连线法的查找的时间复杂度是O（h）---h是树的高度，合并的时间复杂度是：O（h），因为同样要找到两个东西的根，之后才能替换。

 

 其实就相当于是9的根，不再是自己了，而是指向6，因为根的parent是自己，把它改成是别人。

 

共有n个元素，最多有n个集合，所以的话用n个空间的数组足够去标记它属于哪个集合。

 

 

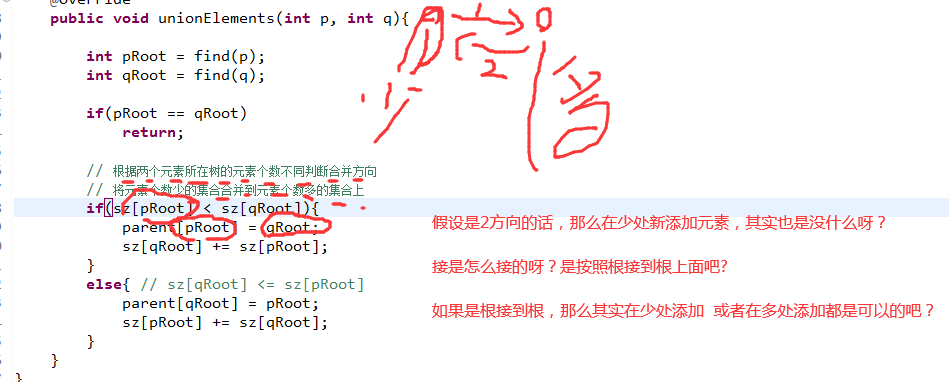
对于size的引入的目的：

 

 如果说左边的根盲目地等于右边的根，以此来进行union操作的话，最坏情况下，它是线性增长的。

因此：需要引入size来规范它最坏情况下的增长。

 

 总是将小的树依附在大的树上

由于查找操作，对于连线法而言，总是依赖于树的高度，才能查找到一个元素所属的集合   以及两个元素是否处于同一个集合。

所以说可以防止树的高度的线性增长。

 

 

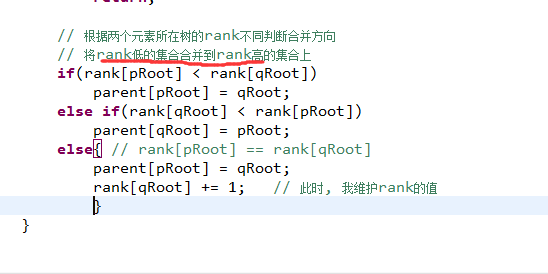
 这个是引入rank的原因：

由于size未必一定能够反映树的高度的真实情况   

rank表示的是  以root为根，它的高度为多少，更加真实地反映了

rank低的树应该依附到rank高的树上

 

所以以后都是用rank，都是用连线法，用树的表示法来表示并查集最为好。  （比分类法更好）

 

 

 

 

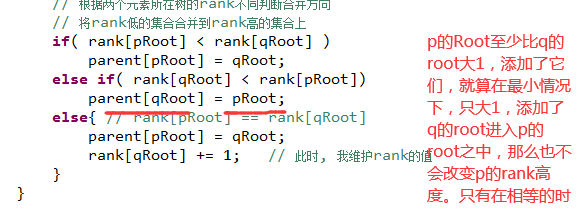
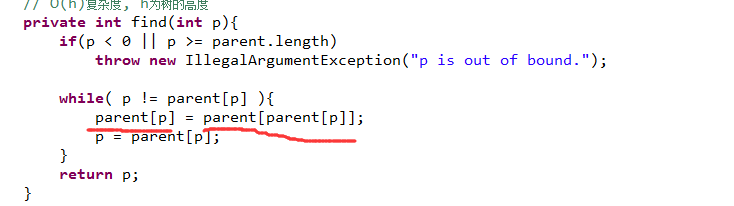
 此处的话，不仅仅向上找，我还更新你。

即：我找一个p的所在的集合的时候，如果发现p的上层q

想象：递归地返回了这个parent[p]

当它们不相等的时候，  即：    p不是根的话，那么就对它的小老大找到真正的老大。

 

函数定义：为p节点，找到真正的老大。

如果说自己不是老大，那么就把自己的老大，更新成最终的老大。

          自己不是老大的情况，把自己的老大，更新为最终的老大。

 

 

 

 

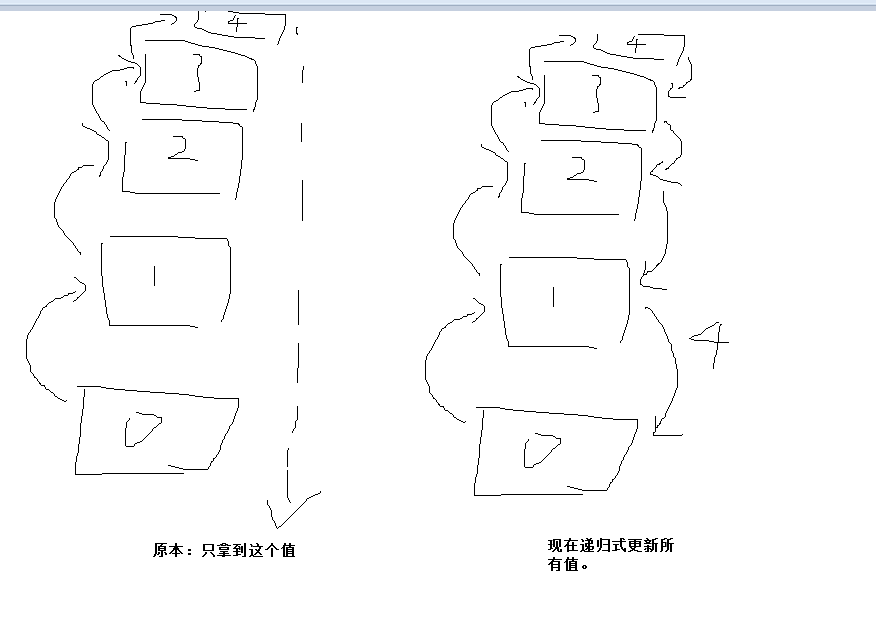
启发：       路径压缩类，如果是链式或者说树状的结构  需要压缩路径的样式  在寻找终点时压缩路径的样式

那么使用递归式返回值是很需要的。

 

压缩路径，递归式返回、更新值可以用      递归的方法。

 

 

 

去找它的父的时候，为p找到真正的根。

一想到递归式使用，就立马展开这个图的想像。现在要很熟练地想到这种方法来使用是困难的，但是有点灵感放在脑袋里，对于递归式返回值的设计有好处。

 

 

 

 感觉这个非递归的方法，不太好诶：

 

 

 

 为什么加权下，是 logN的搜索度呢？

因为的话不可能退化为是线性的了。

 

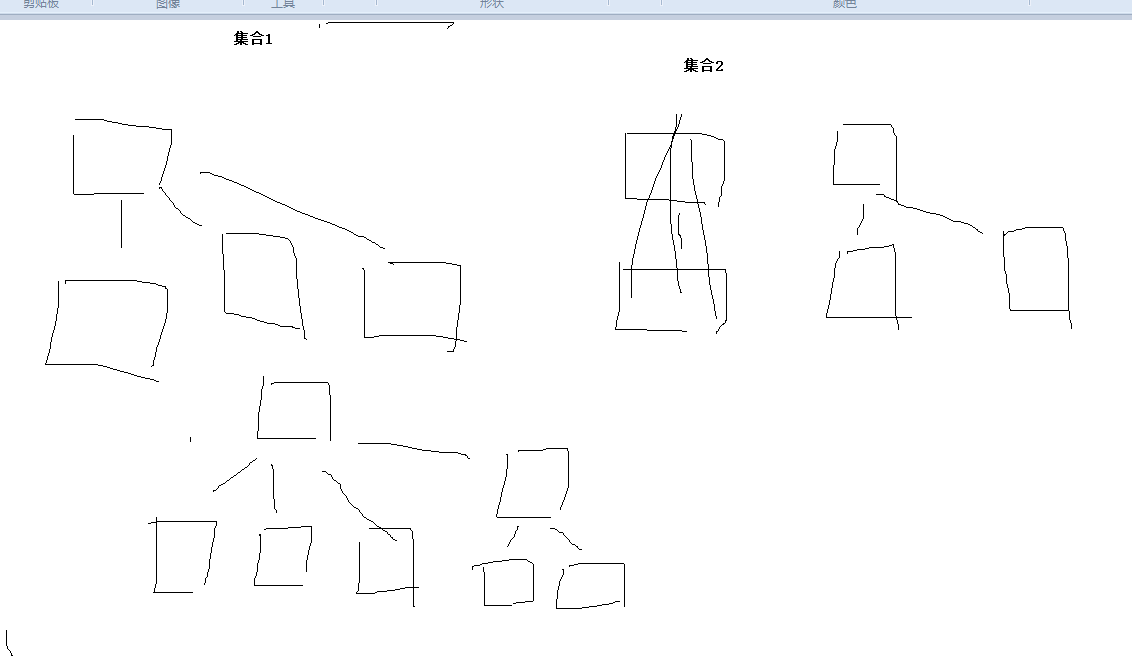
 这里的话，意思是说： 

任意的集合，都是长成这样子的，因为对于每一个的添加进来，都是往新的方向去依附。

所以说会使得搜索的复杂度变成了logN  因为搜索的复杂度变成了logN   所以说union也是logN

 

学习到：

如果说集合这件事情，想要学习：

  查找两个元素是否处于同一个集合    集合数为n    集合里面的元素假设都是m的话，    那么集合查找某个元素是否在这个集合里面，可能是m，可能是logM

那么应该就是     n logM的时间复杂度了。

 

  对两个集合进行合并的操作（如果说用数组的话，那么也是对最小的     一个个遍历，都添加进去，是（N））的复杂度

现在我能够学会的，也只是用二叉搜索树来减小时间复杂度了吧。

 

但是这里学会的是一种方法，减小时间消耗，来减小：

搜索一个元素所在的集合的时间复杂度  logN  乃至到log1，找到所在集合就能合并。

查找两个元素是否处于同一个集合的方法，  logN乃至于log1。

将两个集合进行合并的操作  logN乃至于log1。

 

现在大概只是隐隐约约地感受到了一些并查集可能可以用到的地方，先实现并查集吧。（合并查找  就是 并查集   可以使用一下并查集）