学习数据结构的第八天（三）（包括一些以后学习的指引）

学习一下堆、优先队列、AVL树。

是哪一步就做哪一步的事情，关于项目的经验这些东西，是不是要报培训班这件事情应该怎么办呢？

去知乎搜索相应的问题，然后的话力扣开源代码看懂作为经验之类的。

key：是哪步就做哪步的事情，不需要过分忧虑，也不需要过分安逸。按部就班

 

实现堆以及优先队列后，做完leetcode  topK的题目  

学习树的相关知识，就是什么节点和子节点的关系之类的

然后学习AVL树的内涵是什么

学完数据结构之后刷 剑指offer的题目。

然后廖雪峰博客学习sql基本知识，再学习MVCC等等知识。

廖雪峰微博还有关于servelet之类的知识，学完一些基本的再去看相应的项目

其中可以看知乎回答里面提及的内容。

主要是现在，能够自己管理好自己，对于手机的问题，迅速关闭不留时间给拖延症，是很好的办法（已经持续1周+，有用）

只管做好自己的事，其他随缘。

 

 

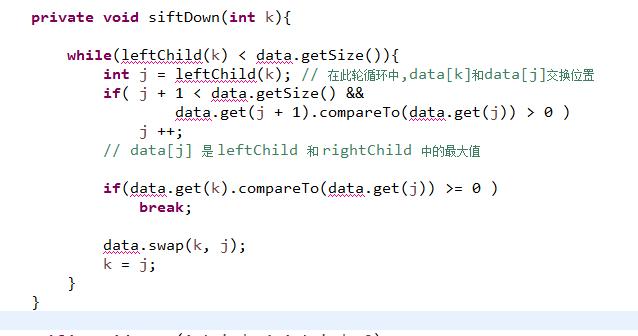
1.对于siftDown这件事： 由于和siftUp不同，siftUp只能往一个方向，即：往上，siftDown 可以选择左子树或者右子树，是不一样的。

2.因此：对于这种做法：  siftDown的想法是：先选择left和right中较大的部分，再进行比较。

3.对于左为空，右为空，左右都不为空这种情况，还是确实很重要。对此，这里的处理方法是：先找其中左子树，如果说左子树没有达到出口条件，那么就认为没有达到出口条件。

然后的话再看右边有没有达到出口条件，再进行指针是否需要加一的想法。

 

学习到的东西先记录：

 

 

 

 

 

 

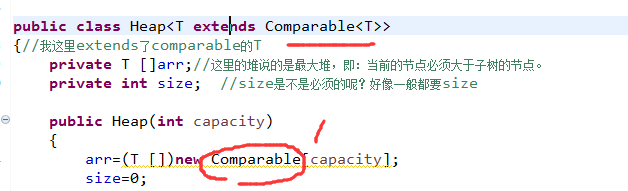
对于此处而言，因为heap必须有比较的操作，因此用new  Comparable的方式来进行构造，而不是new Object

 

 

 

对于此处heap占有的是：  一个数组，就是说数组的底层存储是数组即可

key：作为这个自写的ArrayList来存储可以吗？其实也是ok的，但是似乎觉得没必要。

 

 

 

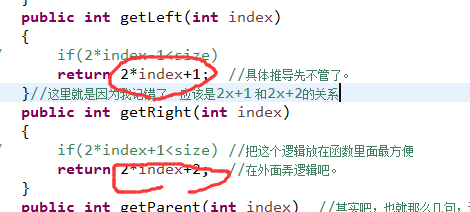
对于左子节点和右子节点分别是：2 x+1 以及2x+2 的关系。

即：知道了heap里面左右子节点推导父节点 以及说父节点推导子节点

 

(6-1)/2=2   在java里面，是对的，

4/5=0       在java里面，是对的，  

 意思是说：在java里面是地板除，两个整数相除，无论多接近top那个整数，都是往地板去靠   0.8往0靠，2.5往2靠。

 

heap意思是说：根节点必定大于它的子节点，或者说根节点必定小于它的子节点。

 

 对于siftUp而言，其实意思是：没有交换即可以停止的了。

对于siftDown也是一样，不需要一定到达根或者到达最末

原因：其实和我之前说的一样，只需要接口处满足条件即可，接口处满足条件，那么上层和下层必定也满足条件。

所以说只需sift到相应的位置，满足大小的关系即可break；

 

 

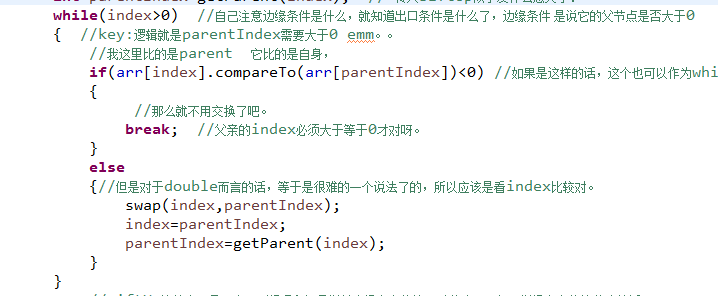
对于这段代码，其实的话我认定： while的循环体，要写什么东西，意思是说，在哪个位置出循环。肯定是拿最接近出循环的边界条件来看。

即：如果它和它的父节点比较，那么应该拿父节点是否大于0作为边界条件。  如果它和它的子节点比较，那么应该拿它的子节点是否小于size作为边界条件。

但是这里为什么用 index>0  而不是parentIndex>=0呢？

原因：parentIndex=(index-1)/2     如果为0的时候 ，正常计算是：-0.5   它的输出是0     

 

意思是：  对于整数的除法而言，java里面是往0靠的。  2.5往2靠，-0.5往0.  也就是说  java往0靠。

对于边界条件而言，（0-1）/2的话，那么是输出0

也就是说：此处当然是看parentIndex 如果说小于0了，那么就是出界。但是由于整数除法的特征，那么还是用index>0作为边界条件 。

原因：除了index=0的时候没有根，其他都有根。

 

意思是：

从子节点求父节点时，通过减法和除法的时候，需要注意相应的出口条件。

 对于加的这种，不是往0靠的，那么不用怕

 

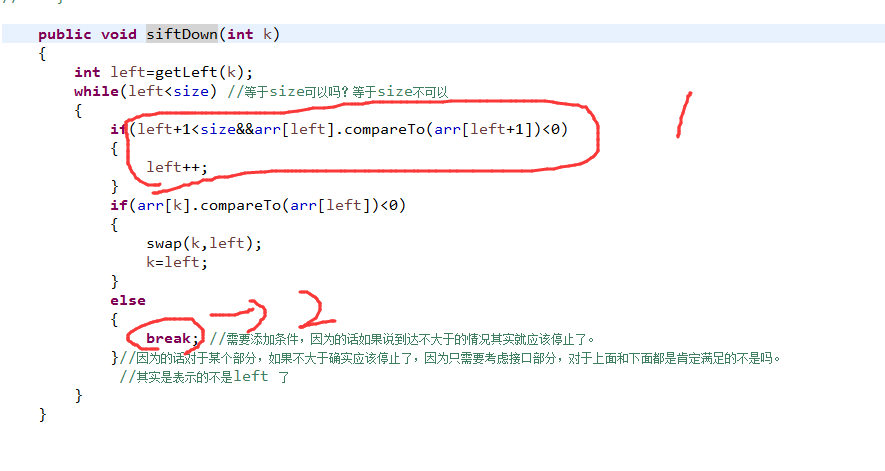
 对于siftDown而言，由于存在：右子树可能不存在问题，左右都可能不存在问题。

所以说先挑其中一边，如果说另外一边更大的话，更换指针++

即：意思是：如果说有多个选择，那么可以先挑一边再说。此处出口条件是这个left是更接近临界的，所以说就是left <size作为临界。

 

 

 对于remove函数而言，意思就是把arr[0]和这个末尾元素交换，并且siftDown的结果

对于add而言，意思就是：在最后面添加元素，并且siftUp

 

 

 

 

这里说的是移动性操作：

 

 

也就是说 从size-1出发  一直到大于index位置，  都进行移动的操作。（和0到size一样，都是=0开始，小于size结束）

定了尾和头之后，再定移动方法，此处为： i=i-1的方法。