基础算法 —— 3. 动态规划

方法论

Like the divide-and-conquer method. But in contrast dynamic programming applies when the subproblems overlap. A dynamic-programming algorithm solves each subsubproblem just once and then saves its answer in a table. We typically apply dynamic programming to optimization problems.

we follow a sequence of four steps:

1. Characterize the structure of an optimal solution.
2. Recursively define the value of an optimal solution.
3. Compute the value of an optimal solution, typically in a bottom-up fashion.
4. Construct an optimal solution from computed information.

优化问题才具有最优子结构，即具有性质：利用子问题的最优结果可以组合成原问题的最优结果 才可以使用动态规划。

一般而言，思考时使用递归的方式，实现时可以用递归或非递归。

Compute fashion

动态规划的递归实现都是归的过程中解决问题。所以每种动态规划算法都至少有两种实现方式。

top-down with memoization 与 bottom-up method

两种实现方式：一般而言，0自底向上比自顶向下减少常数系数的时间复杂度，因为其不需要递归过程的开销和维护表的状态所需必要变量。而自顶向下可以减少对某些不可能的情况的计算。

Elements of dynamic programming

应用动态规划的两个关键点：optimal substructure and overlapping subproblems.

在它所依赖的所有子问题都得到解决之前，不会考虑子问题。也就是说，在考虑特定阶段时，假设所有子问题的结果都已得出。

1. Optimal substructure if an optimal solution to the problem contains within it optimal
   solutions to subproblems.

   step:

   1. You show that a solution to the problem consists of making a choice.Making this choice leaves one or more subproblems to be solved. 确定转移关系
   2. You suppose that for a given problem, you are given the choice that leads to an
      optimal solution. You do not concern yourself yet with how to determine this
      choice. You just assume that it has been given to you. 做出选择
   3. Given this choice, you determine which subproblems ensue and how to best characterize the resulting space of subproblems.

   characteristic:

   1. how many subproblems an optimal solution to the original problem uses.
   2. how many choices we have in determining which subproblem(s) to use in an
      optimal solution.

   这个阶段考虑的是 最优解的具体结构 和 **最优解的转移关系 **。

   具体结构：要识别刻画问题规模是单变量还是多变量。例如下面的钢棒裁剪问题和最短路径问题，都是单变量，而下面的矩阵链乘问题需要两个变量。

   转移关系：钢棒裁剪问题是只裁一刀分成（i 和 n-i ），产生一个子问题（n-i），不过却有n个备选的 i 。而最短路径问题也只有一个子问题，不同阶段选择不同，A和C 都是4个选择，而B是5个选择。矩阵链乘问题 \(A_{ij}\) 有两个子问题，和 \(j-i\) 个选择。

2. overlapping subproblems

   子问题独立：求最短简单路径和最长简单路径，最短简单路径就是子问题无关，独立的，而最长简单路径子问题求解中是相关的，导致某些求解资源被占用后子子问题不能求解

   子问题重叠：如果子问题不重叠，我们就可以使用分治算法。重叠的话就可以用动态规划防止重复计算。

正确性的证明

You do so by supposing that each of the subproblem solutions is not optimal and then deriving a contradiction. In particular, by “cutting out” the nonoptimal solution to each subproblem and “pasting in” the optimal one, you show that you can get a better solution to the original problem, thus contradicting your supposition that you already had an optimal solution

running time

the running time of a dynamic-programming algorithm depends on the product of two factors: the number of subproblems overall and how many choices we look at for each subproblem.

裁钢棒问题总共有n个子问题，子问题最多有n个备选方案，所以时间复杂度 \(O(n^2)\)

the subproblem graph Each vertex corresponds to a subproblem, and the choices for a subproblem are the edges incident to that subproblem. 用有向图理解动态规划

问题集

矩阵连乘问题

令\(A_{ij}\) 表示矩阵链乘 \(A_{i} A_{i+1} … A_{j}\) 。假设我们找到了一个解决方案，那么最后一次两矩阵相乘肯定为 \(A_{ik} * A_{k+1j} \space \space\space i<=k<j\) 由此，我们将原问题分为两个子矩阵链乘 \(A_{ik},A_{k+1j}\) 。在[i, j) 中寻找使乘法次数最小的 k值。

这样一来分治的思想就很好写。

if(当前只有一个矩阵){
    return 0;
}

int min = 0;
for(int k = i;k<j;++k){
	min = std::min(min,下一层Aik次数+下一层Ak+1j次数+Aik与Ak+1j相乘次数);	
}
return min;

不过注意到有大量的重复计算，子问题重叠的标志，由此，我们可以进一步动态规划。

if(当前只有一个矩阵){
    return 0;
}
if(a[i][j] == 0){
    int min = INT_MIN;
    for(int k = i;k<j;++k){
        min = std::min(min,下一层Aik次数+下一层Ak+1j次数+Aik与Ak+1j相乘次数);	
    }
    a[i][j] = min;
}
return a[i][j];

上面的直接由递归版改造的动态规划也称为 自顶向下的动态规划，带记忆的递归，备忘录法等，下面看看另一种动态规划实现。

for(矩阵链规模从2->n){
	for(对每个规模大小的矩阵链){
		for(对每个矩阵链中可能的k值){
			a[i][j] = min(a[i][j],a[i][k]+a[k+1][j]+两矩阵相乘次数);
		}
    }
}

这种实现也称 自底向上的动态规划，填表法等，其特点就是从小规模问题构造大规模问题。

解结构：通过在上面记录最小值的同时记录k，然后通过下面的方法追溯解

if(当前只有一个矩阵){
    输出当前矩阵标号;
}
else{
    cout<<"(";
    以k为界限，输出左部分；
    以k为界限，输出右部分；
    cout<<")";
}

最长公共子序列

这个题的特点是假设解已经得出，由解的结构入手推理。然后可以自顶向下，设 \(C[i,j]\) 表示X 和 Y 的最长公共子序列的长度。则有 \(C[i,j] = \left\{\begin{array}\\C[i-1,j-1]+1 &X_i=Y_j \\\max(C[i-1,j],C[i,j-1])&X_i!=Y_j\end{array}\right.\)

普通的分治算法和自顶向下动态规划比较像，这块只写动态规划的实现。

if(i<0||j<0){
	return 0;
}
if(a[i][j]未计算){
    if(x[i] == y[j]){
        a[i][j] = 进入下一层(i-1,j-1)  + 1
    }
    else{
        a[i][j] = max(下一层(i-1,j), 下一层(i,j-1));
    }
}
return a[i][j];

自底向上的实现

for(i:n){
	for(j:m){
		if(x[i] == y[j]){
			a[i][j] = a[i-1][j-1];
		}
		else{
			a[i][j] = max(a[i-1][j],a[i][j-1]);
		}
    }
}
return a[n][m];

解的结构，在记录 a[i] [j] 的同时记录是从[i-1][j-1] ; [i-1][j] ; [i][j-1] 三个方向中的哪一个来的

if(i<0||j<0){
	return;
}
else{
	if(从[i-1][j-1] 来的){
		cout<<x[i]; //x[i] == y[i]
	else if(从[i-1][j] 来的){
		进入下一层[i-1][j]
	else{
		进入下一层[i][j-1]
	}
}

最大子段和

前面分治一节写过这个的分治解法，因为分治中有子问题重叠，并且具有最优解结构。所以有进一步使用动态规划优化的可能。

直接想比较困难，不过我们可以稍微换种思路。设输入的序列是 x，令 c[i] 表示含有 x[i] 的最大子段和，那么c[i+1] 要么是x[i+1] 要么是 c[i] + x[i+1] ，两个备选。这样可以求出分别以 i 为尾部元素的最大子段和，由于我们要求的是整个数组的子段和，子段的尾部不确定。之后需要遍历 c 数组，找到最大的一项。

//自顶向下
if(i<0){  //当前只有一个元素
	return 0;
}
if(c[i]未求解){
	c[i] = max(下一层(i-1) + x[i+1],x[i+1]);
}
return c[i];


//自底向上
for(;i<n;++i){   //逐渐增大尾端至n
	c[i+1] = max(c[i]+x[i+1],x[i+1]);
}


//最后都需要遍历一遍 C数组，找到最大的元素。

思考这个算法，在动态规划的过程中，其是 \(O(n)\) 最后一次遍历也是 \(O(n)\) 所以，总时间就是 \(O(n)\) 相较于之前的分治 \(O(nlogn)\) 是一个改进。

解结构：在最后遍历c 数组中，通过最终结果和尾元素下标，根据x数组就能求出起始下标。

图像压缩变位压缩存储

分析这个问题，按照我们的分析步骤，首先我们可以看出最优解结构只需一个变量 n 表示问题规模，再看为了确定最优解的备选共有 \(\min(n,256)\) 个。所以我们可以这样写。

即设 \(F[n]\) 表示当有n个像素时的最优解，\(j\) 表示最后一段有 \(j\) 个像素。 \(b\) 表示最后一段单个像素所占的最大位数。 \(F[n] = \min\limits_{1<=j<=\min(n,256)}(F[n-j]+j*b+11)\)

所以，自顶向下的算法如下

if(如果当前像素个数为0){
	return 0;
}
if(F[n]未求解){
	int min = INT_MAX;
	int b = INT_MIN;
	for(对j所有可能的取值){
		用公式更新b的值
		min = std::min(min,进入下一层(n-j)+j*b+11); //更新当前min 的值 
	}
	将min 赋给F
}
return F[n]

自底向上

for(像素个数规模不断增大(i->n)){
	int min = INT_MIN;
	for(对当前规模所有可能的j值){
		更新b 的值
		min = std::min(min,上一段(F[i-j])+j*b+11);
    }
    F[i] = j;
}
return F[n];

解结构：在真正更新 min 时，记录此时的 i-j 即得到划分下标。

电路布线问题

注意题干要求只是使第一层的排线尽可能多，这样的问题实际上是最大不相交子集。

我们要留意的是如何用数学语言描述问题：可以将每条线的上端点用 i 表示，第i 条线既是第i个端点所在的线，j 表示第 i 条线的另一端点。

接下来考虑如何递推：经过分析可知，一条线只有选或不选两种可能。为了满足不相交的特性。当我们将第 i 条线选入集合内，意味着解中剩下的线的下端点都不能超过 i 所对应的 j 。如果不选，那么问题规模 i 减小。而当前可用的下端 j 不变。

故此，我们可以写出递推关系式。令 \(F[i][j]\) 表示上下端点分别为 i j 时最多的连线数。则 \(F[i][j] = max(F[i-1][j-1]+1,F[i-1][j])\)

//递归版
if(i==0){
	return 0;
}
else if(F[i][j] == 0){
	F[i][j] = max(下一层(i-1,j),下一层(i-1,j-1)+1);
}
return F[i][j];

//非递归版
for(i: 1->n){
	for(j: 1->n){
        F[i][j] = max(F[i-1][j],F[i-1][j-1]+1);
	}
}

解的记录：在max 比较大小时可以记录解。然后可以根据记录的数组进行回溯。

钢棒裁剪问题

我们的思路是将裁一刀钢棒分为两部分，左部分不再切割，而右部分可继续切割、相当于子问题。

所以，刻画问题规模只需要一个变量即钢棒的长度n。而切的这一刀却有n个备选位置。

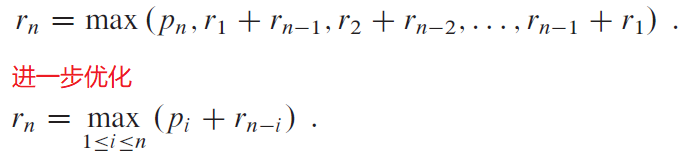
int CutMax_r(int *arr,int n){
    if(n == 0){
        return 0;
    }
    int max = -1;
    for(int i=1;i<=n;++i){
        max = std::max(max,arr[i]+CutMax_r(arr,n-i));
    }
    return max;
}
int CutMax_dT(int *arr,int *brr,int n){
    if(n == 0){
        return 0;
    }
    if(brr[n]==-1){
        for(int i=1;i<=n;++i){
            brr[n] = std::max(brr[n],arr[i]+CutMax_r(arr,n-i));
        }
    }
    return brr[n];
}
int CutMax_dB(int*arr,int *brr,int *s,int n){
    brr[0] = 0;
    for(int i=1;i<=n;++i){
        int res = -1;
        for(int j=1;j<=i;++j){
            if (res < arr[j] + brr[i - j]){
                s[i] = j;
                res = arr[j]+brr[i-j];
            }
            // brr[i] = std::max(brr[i],arr[j]+brr[i-j]);
        }
        brr[i] = res;
    }
    return brr[n];
}
int Trace(int *s,int n){
    while(n>0){
        cout<<s[n]<<' ';
        n -= s[n];
    }
}
int CutMax(int *arr,int n){
    int res = -1;
    // res = CutMax_r(arr,n-1);

    int *brr = new int[n]();
    memset(brr,-1,sizeof(int )*(n));
    int *s = new int[n]();
    memset(s,-1,sizeof(int )*(n));
    // res = CutMax_dT(arr,brr,n-1);
    res = CutMax_dB(arr,brr,s,n-1);
    Trace(s,n-1);
    return res;
}   

子问题：

1. 证明原始递归算法的时间复杂度。

   

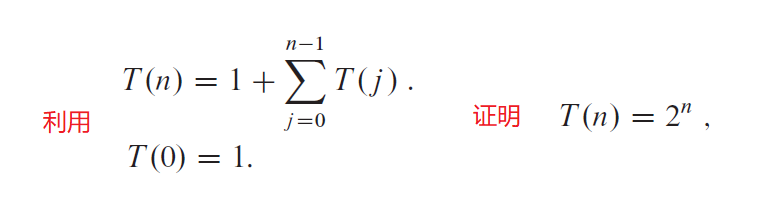
   利用替换法 设 T(n ) <= cn^2.

2. 举反例证明贪心算法在这个问题上不一定能得到最优解。

   问题主要出现在当两种长度的单位价格相同。假设棒的长度为4. 不同尺寸的价值分别为 1，3，6，8 ，那么根据贪心算法，可能选择1-3切，也可能不切，1-3切就不是最优解

3. 加一个条件，每次切割都会有固定的花费。求这种情况下的最优解。

   切一刀的花费可以看做，切一刀的负收益。

4. 修改一下，让它不仅返回解，同时返回解的结构。

   可以将解和解结构封装到结构体里面返回。

5. 通过递归版动态规划实现斐波那契数列的计算。并且子问题图中有多少个节点和多少条边。

   实现没什么好说的，子问题图中有n个节点，2(n-2)条边。

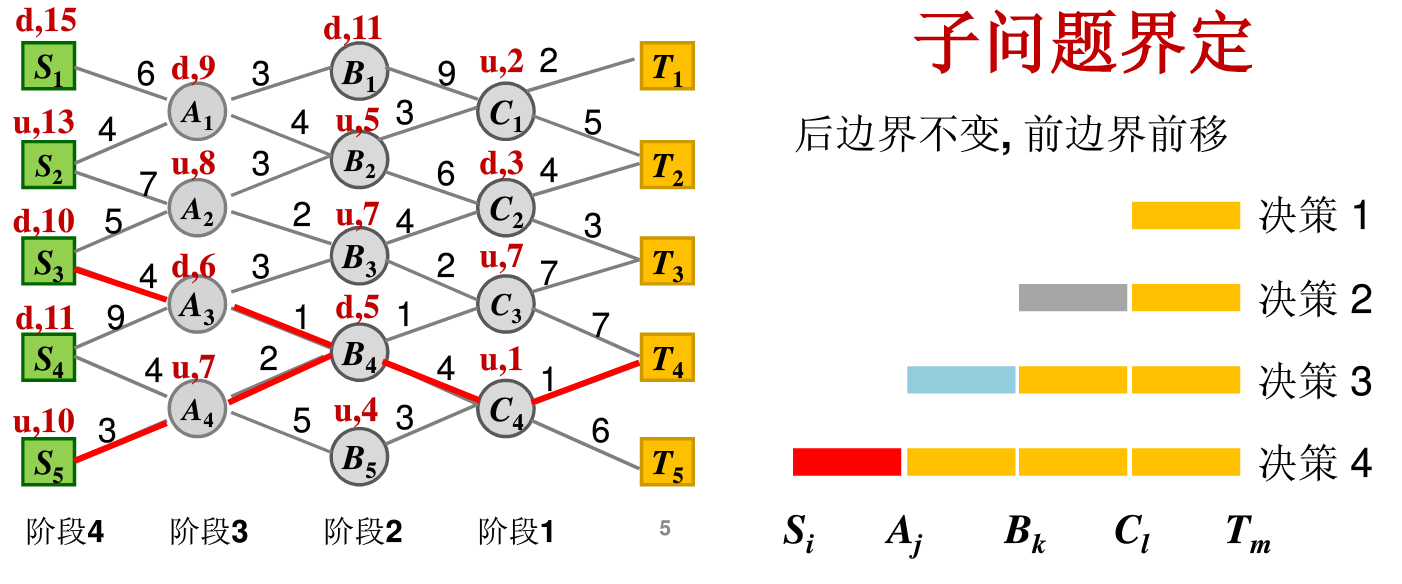
最短路径问题

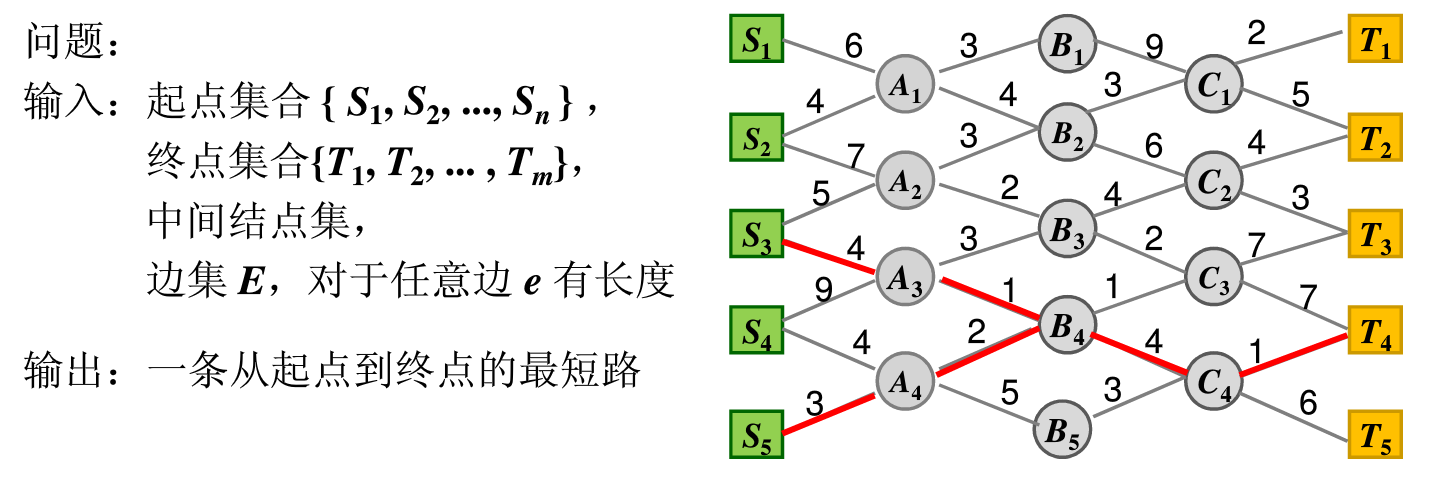
我们选择使终点不变，逐步扩大起点从 C -> S。刻画问题规模只需要一个变量表示阶段数，而本例题每个阶段的有8个备选。

递推方程： S-T 最短 = S-C最短 + C-T 最短

投资问题

我们可以假设 \(F[n][m]\) 表示将m元钱投给n个项目所得的最大收益，那么刻画问题规模需要两个变量，m和n 。而备选的方案 x 要满足 \(0<= x <= \min(f_n,m)\) 其中 \(f_n\) 表示第n 个项目最多投资的钱数。

故此，可得到递推方程 \(F[n,m] = \max\limits_{0<= x <= \min(f_n,m)}(f_n(x)+F_[n-1][m-x])\)

背包问题

背包问题有点大，这里只是简单的提一下简单的三种类型。先从一个例子入手。

有一个背包，\(n\) 个物品，第 \(i\) 个物品的重量和价值分别为 \(w_i\) 和 \(v_i\) ，每个物品只有一件。假设背包总重量限制为 \(b\) 问如何挑选物品使得背包总价值最大。

先说可能的思路，一看到这个问题我第一反应想到了排列问题。一个物品选或不选刚好对应比特位01状态。所以可以用递归模拟二叉树。

现在考虑另一种解法 假设 \(F[n,b]\) 表示有n个物品可供挑选，背包空间为b时的最大收益，那么该问题的状态转移方程可如下定义\(F[n,b] = max(F[n-1,b],F[n-1,b-w[n]]+v[n])\) 等式右边表示装第n 个物品和不装第n个物品的不同收益的最大值。

接下来我们考虑另一个类似问题，假设每个物品有无限件，这时又该如何操作呢？

\(F[n,b] = \max\limits_{0<=k<= \lfloor b/w[n]\rfloor}(F[n-1,b-k*w[n]]+k*v[n] )\) ，如果你令k只能取0-1的话其实这个方程和上面的方程没什么区别。

再推广一下，假设物品的数量不全为1，也不是无限件。那么只需要在上面的方程中对k的值再进一步限定就好。

总结一下对于k 只能取0-1状态的话其实称为0-1背包问题，物品有无限件对应完全背包问题，物品有特定件称为多重背包问题，物品可切片对应 部分背包问题。

关于背包问题更多见 背包九讲