基础算法 —— 1. 算法分析基础

循环不变性

loop invariant 证明算法正确性

• Initialization: It is true prior to the first iteration of the loop.

  在第一次执行赋值操作后，检查真值前的状态。

• Maintenance: If it is true before an iteration of the loop, it remains true before the
  next iteration.

  理解这个循环体。不要拘泥于小细节，例如循环体内嵌套的小循环

• Termination: When the loop terminates, the invariant gives us a useful property
  that helps show that the algorithm is correct.

It's similar to mathematical induction

to prove that a property holds, you prove a base case and an inductive step.

• base case corresponds to the invariant holds before the first iteration.
• inductive step corresponds to the invariant holds from iteration to iteration.
• but the temmination step not simmlar to the mathematical induction .

函数渐进表示法

定义

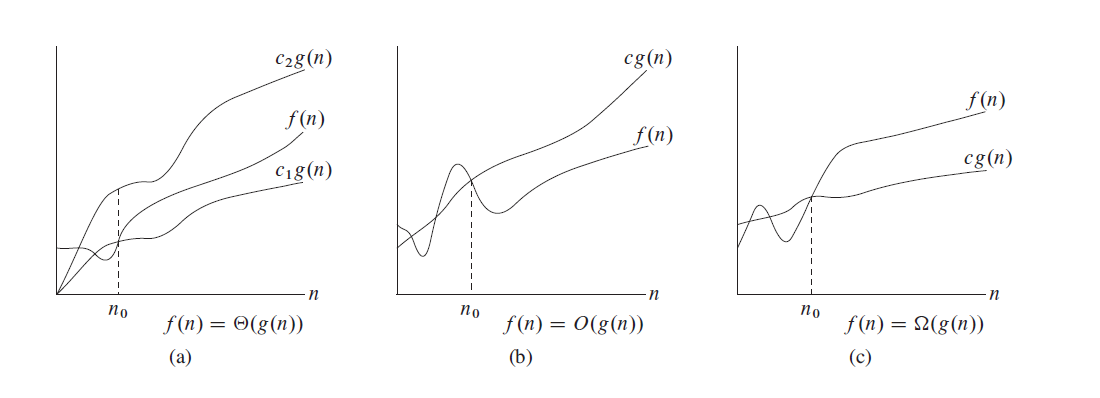
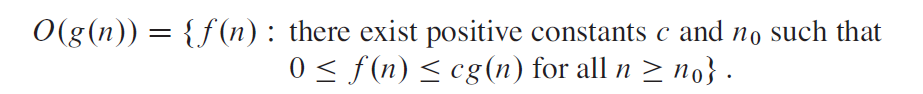
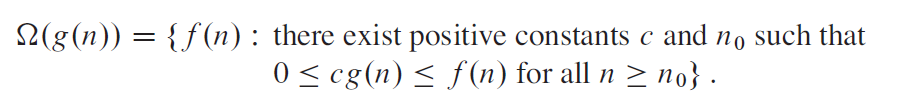
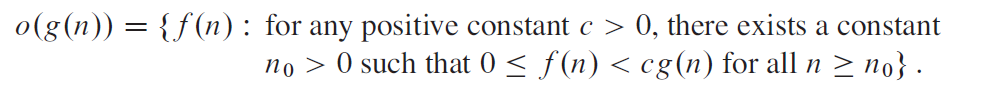
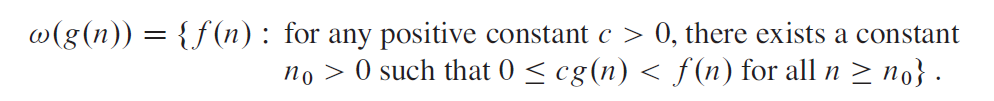
递推公式的计算方法

• substitution method：

  We substitute the guessed solution for the function when applying the inductive hypothesis to smaller values.

  

• recursion-tree method

  

  

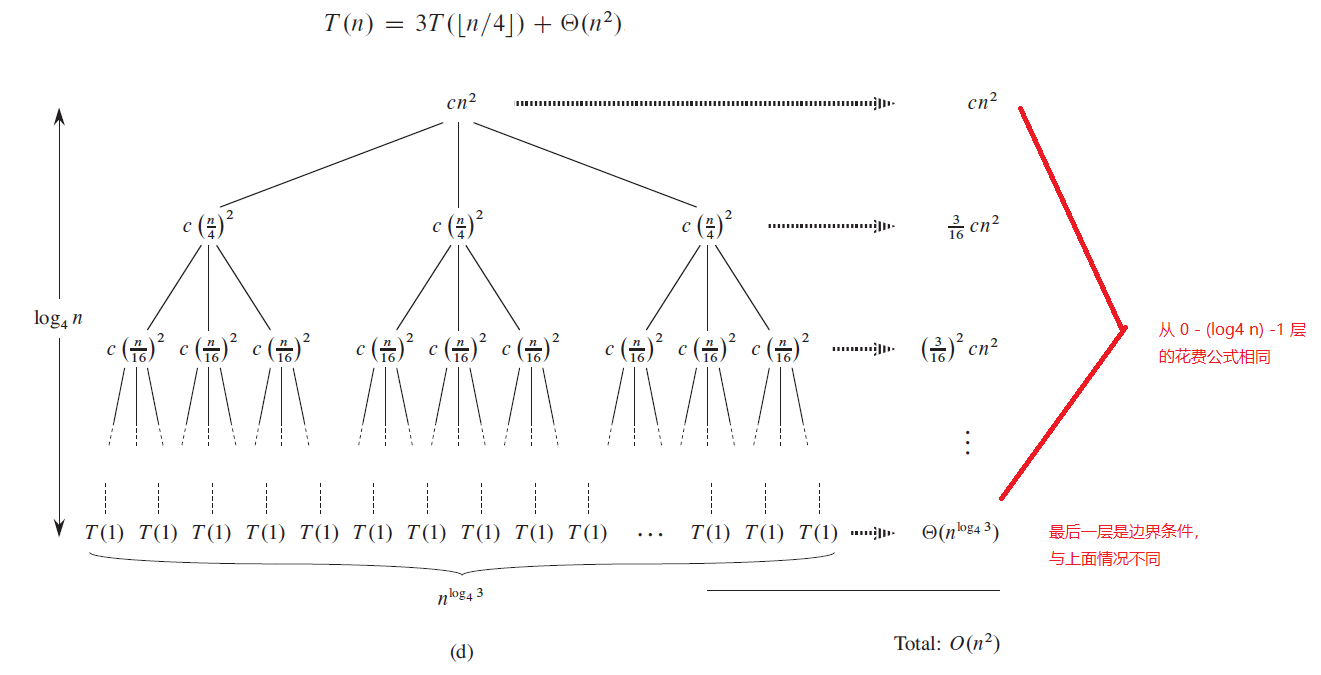
• master method

  

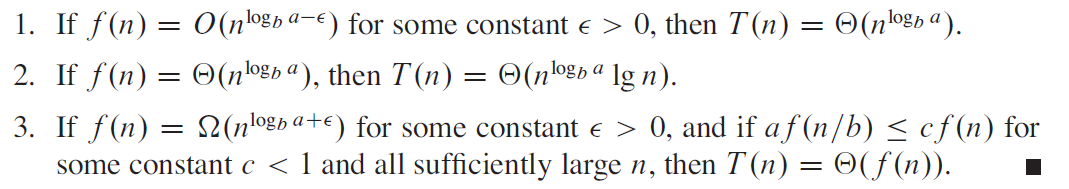
时间复杂度分析

证明时间复杂度，可以用极限。

相应定理运算