布隆过滤器
布隆过滤器
（Bloom Filter）是由布隆（Burton Howard Bloom）在1970年提出的。loom Filter是一种空间效率很高的随机数据结构，它实际上是由一个很长的二进制向量和一系列随机映射函数组成，布隆过滤器可以用于可以快速且空间效率高的判断一个元素是否属于一个集合；用来实现数据字典，或者集合求交集：
一般来讲，计算机中的集合是用哈希表（hash table）来存储的，其好处是快速准确，缺点是费存储空间。当集合较小时，这个问题不显著，但是当集合巨大时，哈希表的存储效率低就显现出来了。
概念
集合表示和元素查询
下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时，Bloom Filter是一个包含m位的位数组，每一位都置为0。
为了表达S={x1, x2,…,xn}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置hi(x)就会被置为1（1≤i≤k）。注意，如果一个位置多次被置为1，那么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一个位置（从左边数第五位）。
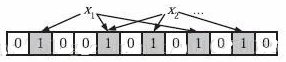
在判断y是否属于这个集合时，我们对y应用k次哈希函数，如果所有hi(y)的位置都是1（1≤i≤k），那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。下图中y1就不是集合中的元素。y2或者属于这个集合，或者刚好是一个false positive。
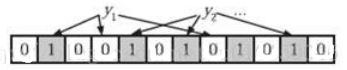
如果想判断一个元素是不是在一个集合内，一般想到的是将所有元素保存起来，然后通过比较确定。链表，数等数据结构都是这种思路。但是随着集合中元素的增加，需要的存储空间越来越大，检索速度越来越慢。
不过世界上还有一种叫作散列表（又叫哈希表，Hash table）的数据结构。它可以通过一个Hash函数将一个元素映射到一个位阵列中的一个点，这样一来我们只要看看这个点是不是 1就知道可以集合中有没有它了。这就是布隆过滤器的基本思想。
Hash面临的问题是冲突。假设Hash函数是良好的，如果我们的位阵列长度为m个点，那么如果想将冲突率降低到1%，这个散列表只能容纳m/100个元素，显然这就不叫空间有效了，解决的方法也很简单，就是使用多个Hash函数，如果它们有一个说元素不在集合中，那肯定就不在，如果它们都说在，虽然有一定可能性它们在说谎，不过直觉上判断这种事情的概率还是比较低的。
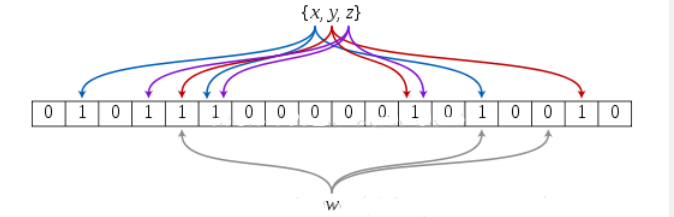
布隆过滤器处理流程
布隆过滤器应用很广泛，比如垃圾邮件过滤，爬虫的url过滤，防止缓存击穿等等。下面就来说说布隆过滤器的一个完整流程，相信读者看到这里应该能明白布隆过滤器是怎样工作的。
第一步：开辟空间
开辟一个长度为m的位数组（或者称二进制向量），这个不同的语言有不同的实现方式，甚至你可以用文件来实现。
第二步：寻找hash函数
获取几个hash函数，前辈们已经发明了很多运行良好的hash函数，比如BKDRHash，JSHash，RSHash等等。这些hash函数我们直接获取就可以了。
第三步：写入数据
将所需要判断的内容经过这些hash函数计算，得到几个值，比如用3个hash函数，得到值分别是1000，2000，3000。之后设置m位数组的第1000，2000，3000位的值位二进制1。
第四步：判断
接下来就可以判断一个新的内容是不是在我们的集合中。判断的流程和写入的流程是一致的。
误判问题
布隆过滤器虽然很高效（写入和判断都是O(1)，所需要的存储空间极小），但是缺点也非常明显，那就是会误判。当集合中的元素越来越多，二进制序列中的1的个数越来越多的时候，判断一个字符串是否在集合中就很容易误判，原本不在集合里面的字符串会被判断在集合里面。
数学推导
布隆过滤器原理十分简单，但是hash函数个数怎么去判断，误判率有多少？
假设二进制序列有m位，那么经过当一个字符串hash到某一位的概率为：
1
也就是说当前位被反转为1的概率：
(1)=1
那么这一位没有被反转的概率为：
(0)=1−1
假设我们存入n各元素，使用k个hash函数，此时没有被翻转的概率为：
(0)=(1−1)
那什么情况下我们会误判呢，就是原本不应该被翻转的位，结果翻转了，也就是
(误判)=1−(1−1)
由于只有k个hash函数同时误判了，整体才会被误判，最后误判的概率为
(误判)=(1−(1−1))
要使得误判率最低，那么我们需要求误判与m、n、k之间的关系，现在假设m和n固定，我们计算一下k。可以首先看看这个式子：
(1−1)
由于我们的m很大，通常情况下我们会用2^32来作为m的值。上面的式子中含有一个重要极限
lim→∞(1+1)=
因此误判率的式子可以写成
(误判)=(1−()−/)
接下来令=−/，两边同时取对数，求导，得到：
′1=(1−)+(−)1−
让′=0，则等式后面的为0，最后整理出来的结果是
(1−)(1−)=
计算出来的k为2，约等于0.693，将k代入p(误判)，我们可以得到概率和m、n之间的关系，最后的结果
(1/2)2，约等于0.6185/
以上我们就得出了最佳hash函数个数以及误判率与mn之前的关系了。
