空间点到直线垂足坐标的解算及C++实现
转自:http://blog.csdn.net/zhouschina/article/details/14647587
假设空间某点O的坐标为(Xo,Yo,Zo),空间某条直线上两点A和B的坐标为:(X1,Y1,Z1),(X2,Y2,Z2),设点O在直线AB上的垂足为点N,坐标为(Xn,Yn,Zn)。点N坐标解算过程如下:
首先求出下列向量:
向量AB可以用方向向量代替
由向量垂直关系:
点N在直线AB上,根据向量共线:
由(2)得:
 (3)
(3)
把(3)式代入(1)式,式中只有一个未知数k,整理化简解出k:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | // 二维空间点到直线的垂足 struct Point { double x,y; } Point GetFootOfPerpendicular( const Point &pt, // 直线外一点 const Point &begin, // 直线开始点 const Point &end) // 直线结束点 { Point retVal;
double dx = begin.x - end.x; double dy = begin.y - end.y; if(abs(dx) < 0.00000001 && abs(dy) < 0.00000001 ) { retVal = begin; return retVal; }
double u = (pt.x - begin.x)*(begin.x - end.x) + (pt.y - begin.y)*(begin.y - end.y); u = u/((dx*dx)+(dy*dy));
retVal.x = begin.x + u*dx; retVal.y = begin.y + u*dy;
return retVal; } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | // 三维空间点到直线的垂足 struct Point { double x,y,z; } Point GetFootOfPerpendicular( const Point &pt, // 直线外一点 const Point &begin, // 直线开始点 const Point &end) // 直线结束点 { Point retVal;
double dx = begin.x - end.x; double dy = begin.y - end.y; double dz = begin.z - end.z; if(abs(dx) < 0.00000001 && abs(dy) < 0.00000001 && abs(dz) < 0.00000001 ) { retVal = begin; return retVal; }
double u = (pt.x - begin.x)*(begin.x - end.x) + (pt.y - begin.y)*(begin.y - end.y) + (pt.z - begin.z)*(begin.z - end.z); u = u/((dx*dx)+(dy*dy)+(dz*dz));
retVal.x = begin.x + u*dx; retVal.y = begin.y + u*dy; retVal.y = begin.z + u*dz;
return retVal; } |



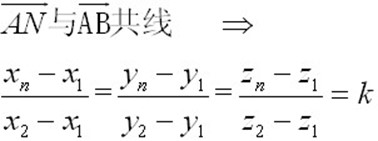


 浙公网安备 33010602011771号
浙公网安备 33010602011771号