05. 感知机

一、感知机

  感知机（Perceptron）是二分类模型，它接收多个信号，输出一个信号。感知机的信号只有 0、1 两种取值。

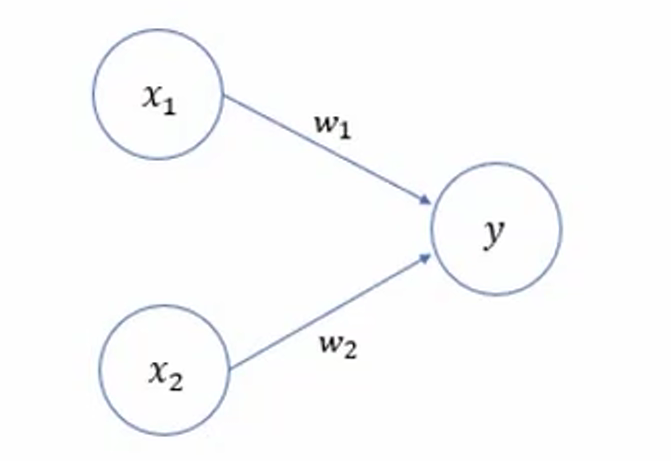
  其中，\(x_{1}\)、 \(x_{2}\) 是 输入信号，y 是 输出信号，\(w_{1}\)、\(w_{2}\) 是 权重，\(\circ\) 称为 神经元 或 节点。输入信号被送往神经元时，会分别乘以固定的权重。神经元会计算传入过来的信号总和，只有当这个总和超过某个界限值时才会输出 1，也称为 神经元被激活。这里将界限值称为阈值 \(\theta\)。

\[y = \begin{cases} 0 & (w_{1}x_{1} + w_{2}x_{2} \le \theta) \\ 1 & (w_{1}x_{1} + w_{2}x_{2} \gt \theta) \end{cases} \]

  感知机的多个输入信号都有各自的权重，这些权重发挥着控制各个信号的重要性的作用，权重越大，对应信号的重要性越高。

二、简单逻辑电路

2.1、与门

  与门是具有两个输入和一个输出的门电路，仅在两个输入均为 1 时输出 1，其它时候输出 0。这种输入信号和输出信号对应表称为真值表。

\(x_{1}\)	\(x_{2}\)	\(y\)
0	0	0
1	0	0
0	1	0
1	1	1

  使用感知机表示与门需要确定能满足上述真值表的 \(w_{1}\)、\(w_{2}\)、\(\theta\) 的值，满足条件的参数有无数个，如 \((w_{1}, w_{2}, \theta) = (0.5, 0.5, 0.7)\)。

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    result = x1*w1 + x2*w2
    return 1 if result > theta else 0

print(AND(0, 0))
print(AND(1, 0))
print(AND(0, 1))
print(AND(1, 1))

  后面为了方便使用向量或矩阵，我们按照线性方程的方式转换为另一种形式，将 \(\theta\) 换成 -b（偏置），表示感知机的公式变为如下格式：

\[y = \begin{cases} 0 & (b + w_{1}x_{1} + w_{2}x_{2} \le 0) \\ 1 & (b + w_{1}x_{1} + w_{2}x_{2} \gt 0) \end{cases} \]

  我们可以在终端中使用 pip 安装 Numpy。默认是从国外的主站上下载，因此，我们可能会遇到网络不好的情况导致下载失败。我们可以在 pip 指令后通过 -i 指定国内镜像源下载。

pip install numpy -i https://mirrors.aliyun.com/pypi/simple

  国内常用的 pip 下载源列表：

• 阿里云 https://mirrors.aliyun.com/pypi/simple
• 中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple
• 清华大学 https://pypi.tuna.tsinghua.edu.cn/simple
• 中国科学技术大学 http://pypi.mirrors.ustc.edu.cn/simple

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    result = w @ x + b
    return 1 if result > 0 else 0

print(AND(0, 0))
print(AND(1, 0))
print(AND(0, 1))
print(AND(1, 1))

2.2、或门

  或门是具有两个输入和一个输出的门电路，只要有一个输入为 1 时输出 1，其它时候输出 0。这种输入信号和输出信号对应表称为真值表。

\(x_{1}\)	\(x_{2}\)	\(y\)
0	0	0
0	1	1
1	0	1
1	1	1

  使用感知机表示与门需要确定能满足上述真值表的 \(w_{1}\)、\(w_{2}\)、\(\theta\) 的值，满足条件的参数有无数个，如 \((w_{1}, w_{2}, \theta) = (0.5, 0.5, 0)\)。

import numpy as np

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    result = w @ x + b
    return 1 if result > 0 else 0

print(OR(0, 0))
print(OR(1, 0))
print(OR(0, 1))
print(OR(1, 1))

2.3、与非门

  与非门是具有两个输入和一个输出的门电路，仅在两个输入均为 1 时输出 0，其它时候输出 1。这种输入信号和输出信号对应表称为真值表。

\(x_{1}\)	\(x_{2}\)	\(y\)
0	0	1
0	1	1
1	0	1
1	1	0

  使用感知机表示与门需要确定能满足上述真值表的 \(w_{1}\)、\(w_{2}\)、\(\theta\) 的值，满足条件的参数有无数个，如 \((w_{1}, w_{2}, \theta) = (-0.5, -0.5, -0.7)\)。

import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    result = w @ x + b
    return 1 if result > 0 else 0

print(NAND(0, 0))
print(NAND(1, 0))
print(NAND(0, 1))
print(NAND(1, 1))

三、多层感知机

  异或门是具有两个输入和一个输出的门电路，当两个输入相同时输出 0，不同时输出 1。这种输入信号和输出信号对应表称为真值表。

\(x_{1}\)	\(x_{2}\)	\(y\)
0	0	0
0	1	1
1	0	1
1	1	0

  我们结合感知机公式和异或门的真值表可得：

\[y = \begin{cases} 0 \le \theta) \\ w_{1} \gt \theta \\ w_{2} \gt \theta \\ w_{1} + w_{2} \le \theta \end{cases} \]

  上述的公式无法同时满足，因此我们无法使用一个感知机实现异或门。我们可以用多层感知机实现异或门。

  与门与非门或门符号表示：

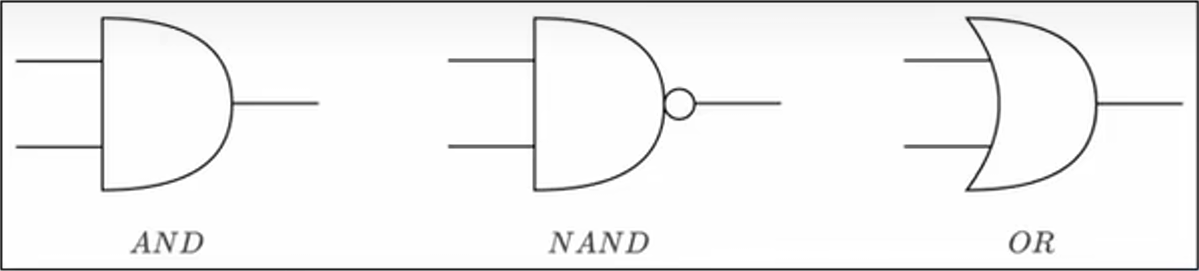
  我们可以将它们组合实现一个异或门。

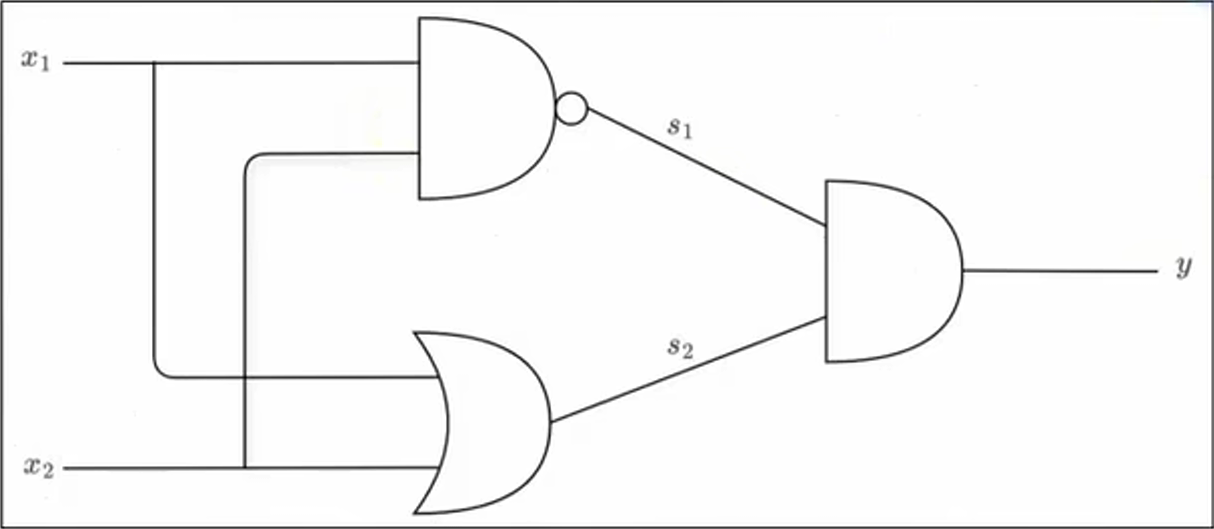
\(x_{1}\)	\(x_{2}\)	\(s_{1}\)	\(s_{2}\)	\(y\)
0	0	1	0	0
0	1	1	1	1
1	0	1	1	1
1	1	0	1	0

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    result = w @ x + b
    return 1 if result > 0 else 0

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    result = w @ x + b
    return 1 if result > 0 else 0

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    result = w @ x + b
    return 1 if result > 0 else 0

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

print(XOR(0, 0))
print(XOR(1, 0))
print(XOR(0, 1))
print(XOR(1, 1))

一层感知机的局限性在于它只能由一条直线划分的空间。由直线划分的空间的称为 线性空间，由曲线划分的空间称为 非线性空间。