后缀数组简介与Golang实现

后缀数组（suffixarray）用来解决一系列与字符串模式匹配相关的问题。因为我比较菜，也不是ACMer，因此本文主要用来给自己扫盲，非常简单

 

先介绍几个概念：

sa: 后缀数组。将原字符串（长度为n）的所有n个后缀按字典序排名，sa[i]=k表示排名为i的后缀在原字符串中的起始下标为k。简记：sa是排名的下标

rk：排名数组。rk[i]=k表示原字符串的起始下标为i的后缀在所有后缀的字段序排名中排在第k个。简记：rk是下标的排名。显然，sa[rk[i]]=i。本文排名从1开始，下标从0开始，所以本文中sa[rk[i]-1]=i

height：高度数组。height[i]=LCP(sa[i], sa[i-1])，即排名相邻的两个后缀的最长公共前缀（LCP，longest common prefix）

 

给出一个例子，直观地展示这三个概念。

原字符串：banana。

所有后缀的按字典序排名：a, ana, anana, banana, na, nana

第0个后缀(banana)的排名为4，rk[0]=4，sa[4-1]=0

第1个后缀(anana)的排名为3，rk[1]=3，sa[3-1]=1

第2个后缀(nana)的排名为6，rk[2]=6，sa[6-1]=2

第3个后缀(ana)的排名为2，rk[3]=2，sa[2-1]=3

第4个后缀(na)的排名为5，rk[4]=5，sa[5-1]=4

第5个后缀(a)的排名为1，rk[5]=1，sa[1-1]=5

故sa=[5, 3, 1, 0, 4, 2], rk=[4, 3, 6, 2, 5, 1]

然后按照定义求height数组。

""与"a"的LCP长度为0，height[0]=0

"a"与"ana"的LCP长度为1，height[1]=1

"ana"与"anana"的LCP长度为3，height[2]=3

"anana"与"banana"的LCP长度为0，height[3]=0

"banana"与"na"的LCP长度为0，height[4]=0

"na"与"nana"的LCP长度为2，height[5]=2

故height=[0, 1, 3, 0, 0, 2]

 

接下来介绍如何求sa

朴素的做法显然是列出所有后缀，然后对它们排序（假如是快排）

写出递归方程：T(n)=2T(n/2)+O(n²)，因此复杂度是O(n²)

注：n²是怎么来的？原版快排中，n个数和pivot都要做比较，为O(n)，但这里不是数字比较而是字符串比较，字符串长n，比较n次，复杂度O(n²)。根据主定理，总复杂度是O(n²)。看到有人说：“快排是O(nlogn)，字符串比较是O(n)，总复杂度是O(n²logn)”，显然是错的。

 

一种最简单、最常见的优化方法：倍增法(binary lifting)来求sa，复杂度是O(nlogn)

思路是分治法。

先对所有长为1的子串求出它们的排名

假设已经计算出了所有长为k的子串的排名，那么位置相邻的两个子串可以组成新的长为k*2的子串，而所有长为k*2的子串的排名可以有组成它的两个子串的排名求得。即先比较第一个子串的排名，如果相等，再比较第二个子串的排名。

长度不为2的幂的子串可以进行补零。

还是举banana的例子。先计算所有长为1的子串的排名

b(2) a(1) n(3) a(1) n(3) a(1)

再将相邻的子串合并为长为2的子串(_表示补零)：

ba(21) an(13) na(31) an(13) na(31) a_(10)

再计算长为2的子串的排名。因为10<13<21<31，所以得到：

ba(3) an(2) na(4) an(2) na(4) a_(1)

再将相邻（注意是在原字符串中的位置相邻）的子串合并为长为4的子串：

bana(34) anan(22) nana(44) ana_(21) na__(40) a___(10)

再计算长为4的子串的排名。因为10<21<22<34<40<44，所以得到：

bana(4) anan(3) nana(6) ana_(2) na__(5) a___(1)

再将相邻的子串合并为长为8的子串：

banana__(45) anana___(31) nana____(60) ana_____(20) na______(50) a_______(10)

再计算长为8的子串的排名。因为10<20<31<45<50<60，所以得到：

banana__(4) anana___(3) nana____(6) ana_____(2) na______(5) a_______(1)

忽略补零，发现这就是所有后缀的字典序排名，即rk。

所以rk=[4, 3, 6, 2, 5, 1]。由sa[rk[i]-1]可求出sa。

 

接下来介绍如何计算height

朴素的做法直接按定义求，要做n次字符串比较，复杂度O(n²)，不考虑。

引理：height[rk[i]] ≥ height[rk[i-1]]-1

不严格地证明：

设k=rk[i-1]-1

height[rk[i]] = LCP(sa[rk[i]], sa[rk[i]-1]) = LCP(i, sa[rk[i]-1])

height[rk[i-1]] = LCP(sa[rk[i-1]], sa[rk[i-1]-1]) = LCP(i-1, k)

设height[rk[i-1]) = LCP(suffix(i-1), suffix(k))

那么存在suffix(k+1)，使得LCP(suffix(i), suffix(k+1)) = LCP(suffix(i-1), suffix(k)) - 1，也就是height[rk[i]]的下界是height[rk[i-1]]-1

有了这个引理，可以在O(n)时间内得到height数组，只需要遍历rk的过程中计算height即可，其中每轮迭代height至多减少1

 

完整代码（Golang）：

package main

import (
	"fmt"
	"sort"
)

type suffix struct {
	c   rune
	idx int // a tuple (c, idx) indicates a suffix in source string
}

type SA struct {
	src    string
	sa     []int
	rk     []int
	height []int
}

func NewSA(src string) *SA {
	n := len(src)
	sa := make([]suffix, n)
	for i, c := range src {
		sa[i] = suffix{c, i}
	}
	// init sa: sort by ascii
	sort.Slice(sa, func(i, j int) bool {
		return sa[i].c < sa[j].c
	})

	rk := make([]int, n)
	// init rk: incr rk each time sa[i].c changes
	rk[sa[0].idx] = 1
	for i := 1; i < n; i++ {
		rk[sa[i].idx] = rk[sa[i-1].idx]
		if sa[i].c != sa[i-1].c {
			rk[sa[i].idx]++
		}
	}

	// binary lifting
	// k is length of substr needed comparing
	// when the last of rk is n, terminate
	for k := 2; rk[sa[n-1].idx] < n; k <<= 1 {
		// sort sa by rank tuple (first, second)
		sort.Slice(sa, func(i, j int) bool {
			ii, jj := sa[i].idx, sa[j].idx
			// compare first part
			if rk[ii] != rk[jj] {
				return rk[ii] < rk[jj]
			}
			// compare second part
			if ii+k/2 >= n {
				return true // special case: second part not exists
			}
			if jj+k/2 >= n {
				return false
			}
			return rk[ii+k/2] < rk[jj+k/2]
		})
		// update rk
		rk[sa[0].idx] = 1
		for i := 1; i < n; i++ {
			cur, pre := sa[i].idx, sa[i-1].idx
			rk[cur] = rk[pre]
			// incr rk each time the substring changes. notice that an out-of-bound case indicates a change
			if cur+k > n || pre+k > n || src[cur:cur+k] != src[pre:pre+k] {
				rk[cur]++
			}
		}
	}
	realSA := make([]int, n)
	for i, v := range sa {
		realSA[i] = v.idx
	}
	// compute height
	height := make([]int, n)
	k := 0
	for i := 0; i < n; i++ {
		if rk[i] == 1 {
			continue
		}
		j := realSA[rk[i]-2]
		if k > 0 {
			k-- // invariant condition: height[rank[i]]>=height[rank[i-1]]-1
		}
		for i+k < n && j+k < n && src[i+k] == src[j+k] {
			k++
		}
		height[rk[i]-1] = k
	}

	return &SA{src, realSA, rk, height}
}

注意，在我上面的代码中，计算sa时，外层循环logn次，每轮一次快排，复杂度O(nlogn)，总复杂度O(nlog²n)。还能用基数排序继续优化，总复杂度O(nlogn)

 

例题1：

 

 

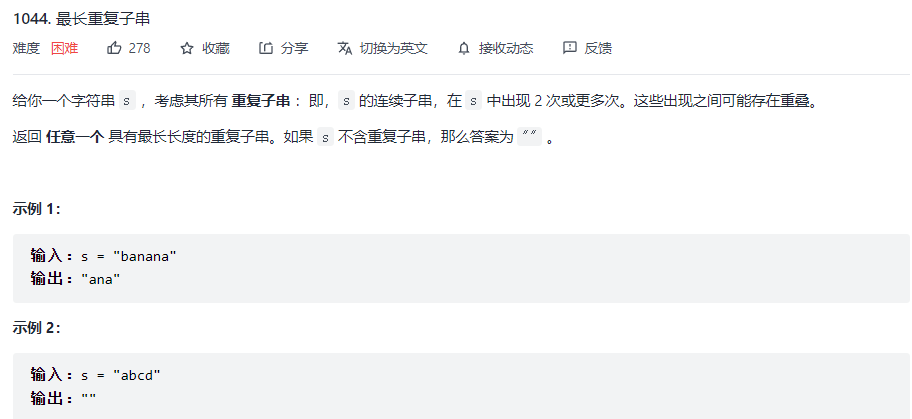
 重复子串必定是原字符串的某两个后缀的LCP，且这两个后缀的字典序相邻（若不相邻，则它们之间的某个后缀可能可以和第一个后缀产生更长的LCP）

所以遍历height数组，找出最大值即可。

func longestDupSubstring(s string) string {
	SA := NewSA(s)
	sa, height := SA.sa, SA.height
	max := 0
	idx := -1
	for i := 1; i < len(s); i++ {
		if max < height[i] {
			max = height[i]
			idx = sa[i]
		}
	}
	if idx == -1 {
		return ""
	}
	return s[idx : idx+max]
}

　　

例题2：模式串匹配

对于串s，找出模式串p在s中出现的所有位置。

考虑s的后缀数组sa

设i是sa的第一个下标，使得s[sa[i]:]>=p （因为sa数组的下标就是排名，所以下标大于i的，字典序排名也大于s[sa[i]:]）

设j是sa的在i之后的第一个下标，使得p不是s[sa[j]:]的前缀（因此sa数组中下标大于j的都不可能是p的前缀，而小于j（且大于i）的都以p为前缀）

那么sa数组中下标大于j的都不可能是p的前缀

由定义，j-1满足s[sa[j-1]:]以p为前缀，而s[sa[i]:]到s[sa[j-2]:]的字典序都不大于s[sa[j-1]:]，所以它们都以p为前缀。

因此，sa[i:j]即为所求。

复杂度：两次二分搜索O(logn)，其中第二次每轮搜索需要比较字符串，复杂度为O(len(p))，故总复杂度为O(len(p)*logn)

func (sa *SA) Match(p string) []int {
	i := sort.Search(len(sa.sa), func(i int) bool {
		return sa.src[sa.sa[i]:] >= p
	})
	j := i + sort.Search(len(sa.sa)-i, func(j int) bool {
		return !strings.HasPrefix(sa.src[sa.sa[i+j]:], p)
	})
	return sa.sa[i:j]
}