NOIP 复习题之最小生成树

[THUPC2022 初赛] 最小公倍树

直接建图复杂度 \(\mathcal O((R-L)^2)\)，但是有很多边可以被忽略。考虑 \(\text lcm(a,b)=\dfrac{a\times b}{\gcd(a,b)}\)，则每次考虑 \(\gcd(a,b)\) 的倍数。

假设枚举的因子是 \(x\)，在 \([L,R]\) 区间内是 \(x\) 的倍数的数有 \(kx,(k+1)x,\dots,(k+p)x\)。则 \((k+1)x,\dots,(k+p)x\) 的数向 \(kx\) 连边是最优的。若 \((k+p)x\) 和某个数 \((k+j)x\) 连边，他们的 \(gcd\) 可能变大了，但是会被更大因子的 \(x\) 所包含。所以最优。总复杂度为调和级数。

CF1120D Power Tree

题意：给定 \(w_i\) 表示可以把 \(i\) 子树内的点的权值增加一个自己选定的 \(v\)。问至少花费多少个节点的 \(w_i\)，使得不管树上点的初始权值是什么，都可以均变为 \(0\)。

做法：先跑 dfn 序，则可以看成用 \(w_i\) 花费使得 \([l_i,r_i]\) 区间的值可以整体修改。区间修改考虑转化成差分：\(c_l\) 加上 \(x\)，\(c_{r+1}\) 减去 \(x\)。容易知道，差分数组的总和不变。但要求 \(c_1,c_2,\dots,c_n\) 都为 \(0\)，则只能把权值转移到 \(c_{n+1}\)。

考虑如果选了 \(i\)，则 \(c_l\) 的权值可以转换到 \(c_{r+1}\)，\(c_{r+1}\) 的权值也可以转换到 \(c_l\)。则让所有数权值都转换到 \(n+1\)，就为如下问题：有 \(n\) 条边 \((l_i,r_i+1,w_i)\)，求最小生成树且和 \(n+1\) 联通。第二个条件，在求出最小生成树后显然是满足的。

这题还有一个子问题：问所有可能在最小生成树上的边的并集。我们把权值从小到大排序，对于 \(w_i\) 相等的边集，如果可以加入，则为可能的答案。

_for(i, 1, tot) {
	int u = ed[i].u, v = ed[i].v, w = ed[i].w;
	int j = i;
	_for(k, i, tot) {
		if (ed[k].w != ed[i].w) break;				
		j = k;
	}
	_for(k, i, j) {
		u = ed[k].u, v = ed[k].v, w = ed[k].w;
		int fx = find(u), fy = find(v);
		if (fx != fy) ans.push_back(ed[k].id);
	}
	_for(k, i, j) {
		u = ed[k].u, v = ed[k].v, w = ed[k].w;
		int fx = find(u), fy = find(v);
		if (fx != fy) {
			res += w;
			p[fx] = fy;
		}
	}
	i = j;
}

[APIO2008] 免费道路

题意：给一个图只有 \(0/1\) 边，求一个生成树恰好包含 \(K\) 条 \(1\) 边。

思路：可能会认为 \(1\) 边是随便加，但其实有些边是必须加的。

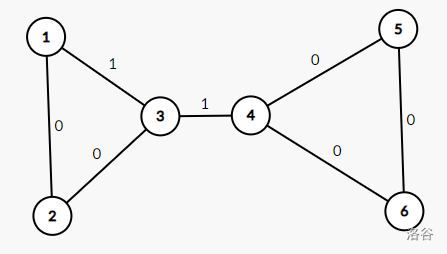
比如上图 \(K=1\)，如果加了 \((1,3)\) 这条边，会导致图不连通。

则先跑一边 Kruskal 将所有 \(0\) 边加入生成树中，再将 \(1\) 边加入生成树，并对这些 \(1\) 边打上标记。此时加入的 \(1\) 边为正确方案之一，也就是肯定满足条件。

然后再跑一边 Kruskal。先加入打上标记的 \(1\) 边，再加入其他的 \(1\) 边使得 \(1\) 边个数达到 \(K\) 条，最后加入 \(0\) 边使得图联通。

HDU4081

先跑一遍最小生成树，考虑 \(n\leq 1000\)，则可以枚举在哪两个点间建立魔法道路。考虑无魔道的道路尽量小，则这条道路替换最小生成树路径上最小权值的边。跑一遍即可。