NOIP 复习题之栈/队列

栈/队列部分

CF1195E

给定一个 $ n\times m $ 的矩阵 $ h $，求出所有大小为 $ a\times b $ 的子矩形中的最小值的和。

思路

对于数组 $h$ 中第 $i$ 行的 $m$ 个数，算出对于每个 $1\leq j\leq m-b+1$ 的 $[j,j+b-1]$ 的最小值，用单调队列可以快速计算。将算出来的值存到 $n$ 行 $m-b+1$ 列的数组 $K$ 中。

再对数组 $K$ 的每一列的 $n$ 个数，算出对于每个 $1\leq i\leq n-a+1$ 的 $[i,i+a-1]$ 的最小值 $x$，将答案对每一个算出的 $x$ 取 min 就是答案。

总结：将矩阵压成一维来考虑。

CF1428F

给定一个 01 串，设 $ f(l,r) $ 为从 $ l $ 到 $ r $ 的子串中，最长的全部为 $ 1 $ 的子串的长度。求 $ \sum_{l=1}^n\sum_{r=l}n f(l,r) $

思路

非常妙的题。考虑固定右端点，算左端点造成的贡献。记 $S_r=\sum_{l=1}^{r} f(l,r)$。现在只需要快速计算出将 $r$ 移动一格后多造成的答案，显然 $S_r$ 单调不降。

如果 $a_r=0$，那么有 $S_r=S_{r-1}$。

否则，找出以 $r$ 结尾的最长连续的 $1$，长度记为 $x$。

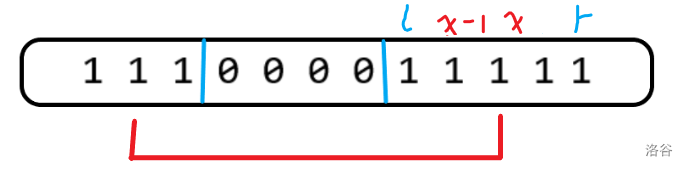
如上图所示，$S_r$ 比 $S_{r-1}$ 只在红色段上多 $1$ 的贡献。红色段的左端点就是最靠右的长度为 $x-1$ 的连续段 $1$。循环一边就可以计算出左端点。

#include <bits/stdc++.h>
using namespace std;

#define int long long
#define PII pair<int, int>
#define _for(i, a, b) for (int i = (a); i <= (b); i++)
#define _pfor(i, a, b) for (int i = (a); i >= (b); i--)

const int N = 5e5 + 5;

int n, f[N], sum, res, tot;
char a[N]; 

signed main() {
	cin >> n >> (a + 1);
	_for(i, 1, n) {
		if (a[i] == '0') {
			_for(j, 1, tot) f[j] = i - j;
			tot = 0;
			res += sum;
		}
		else {  
			sum += i - f[++tot];
			res += sum;
		}
	}
	cout << res << endl;
}

League of Legends 牛客多校

给定 $n$ 个左闭右开区间 $[l_i,r_i)$，试将其不重不漏地分为 $k$ 个非空组，最大化 每个组的区间交的长度 的和。要求每组的交均非空，无解输出 0。

思路：

首先预处理，如果存在一个大区间包含了一个小区间，可以把大区间拿出来。因为这个大区间要么单独成为一个组，要么加入小区间所在的组，对最优解没有影响。预处理完后剩下的就是互不包含的若干区间。

如何看哪些区间包含别的区间：左端点递增排序，若左端点相同，右端点递减排序。然后倒着处理区间，如果当前区间右端点大于之前区间的右端点，就说这个区间是大区间。

剩下就来处理小区间了，很显然的 $dp$：设 $dp_{i,j}$ 表示前 $i$ 个小区间分为 $j$ 组的最大长度和。转移 $dp_{i,j}=\max\{dp_{k-1,j-1}+r_k-l_i\}$。这个 dp 的前提是保证 $r_k>l_i$。这个用单调队列优化 dp 可解决。

我们知道大区间单独一组，所以枚举有 $w$ 个大区间单独一组，加上 $dp_{m,k-w}$ 即可。

#include <bits/stdc++.h>
using namespace std;

#define int long long
#define PII pair<int, int>
#define _for(i, a, b) for (int i = (a); i <= (b); i++)
#define _pfor(i, a, b) for (int i = (a); i >= (b); i--)

const int N = 5005;
int n, k, lst = 2e9, len[N], tot, m, sum[N], dp[N][N], q[N];
struct edge {
	int l, r;
}ed[N], a[N];

bool cmp(edge x, edge y) {
	if (x.l != y.l) return x.l < y.l;
	return x.r > y.r; 
}

signed main() {
	cin >> n >> k;
	_for(i, 1, n) {
		cin >> ed[i].l >> ed[i].r;
		if (ed[i].l == ed[i].r) puts("0"), exit(0);
	}
	sort(ed + 1, ed + n + 1, cmp);
	_pfor(i, n, 1) {
		if (ed[i].r >= lst) {
			len[++tot] = ed[i].r - ed[i].l; 
		}
		else {
			a[++m] = ed[i];
			lst = ed[i].r;
		} 
	}
	sort(len + 1, len + tot + 1, greater<int>{});
	sort(a + 1, a + m + 1, cmp);
	_for(i, 1, tot) sum[i] = sum[i - 1] + len[i];
	memset(dp, -0x3f, sizeof dp);
	dp[0][0] = 0;
	_for(i, 1, k) {
		int l = 1, r = 0;
		_for(j, 1, m) {
			while (l <= r && a[q[l]].r <= a[j].l) l++;
			while (l <= r && a[q[r]].r + dp[q[r] - 1][i - 1] <= dp[j - 1][i - 1] + a[j].r) r--;
			q[++r] = j;
			if (l <= r) dp[j][i] = dp[q[l] - 1][i - 1] + a[q[l]].r - a[j].l;
		}
	}
	int res = 0;
	_for(i, 0, min(tot, k)) {
		res = max(res, sum[i] + dp[m][k - i]);
	}
	cout << res << endl;
}

AT_arc067_d

思路：

可以知道走的路一定是单向，且正着走和反着走一样。枚举 $l,r$ 表示从 $l$ 走到 $r$，然后对于每一张烧烤券，在 $[l,r]$ 烧烤店中选择美味度最大的一个吃。复杂度 $O(n^2m)$，不是最优解。

我们从每张烧烤券造成的贡献来考虑，对于烧烤券 $j$ 来讲，枚举第 $i$ 个店，找到左边第一个用烧烤券 $j$ 美味度大于的店 $L_i$ ，右边第一个用烧烤券 $j$ 大于等于他的店 $R_i$。那么对于起点为 $[L_i+1,i]$，终点为 $[i,R_i-1]$ 的线段，一定会选择第 $i$ 个店。那么二维差分即可！

一边取大于，另一边要取大于等于，不然会漏算或者多算。

#include <bits/stdc++.h>
using namespace std;

#define int long long
#define PII pair<int, int>
#define _for(i, a, b) for (int i = (a); i <= (b); i++)
#define _pfor(i, a, b) for (int i = (a); i >= (b); i--)

const int N = 5005;
int n, m, a[N], b[N][N], l[N], r[N], sum[N][N], res;

void add(int x1, int y1, int x2, int y2, int val) {
	x1++, y1++, x2++, y2++;
	sum[x2][y2] += val;
	sum[x1 - 1][y2] -= val;
	sum[x2][y1 - 1] -= val;
	sum[x1 - 1][y1 - 1] += val;
}

signed main() {
	cin >> n >> m;
	_for(i, 2, n) {
		int x;
		cin >> x;
		a[i] = a[i - 1] + x;
	}
	_for(i, 1, n) _for(j, 1, m) cin >> b[i][j];
	_for(j, 1, m) {
		stack<int> stk;
		_for(i, 1, n) {
			while (stk.size() && b[stk.top()][j] <= b[i][j]) stk.pop();
			if (stk.size()) l[i] = stk.top();
			else l[i] = 0;
			stk.push(i); 
		}
		while (stk.size()) stk.pop();
		_pfor(i, n, 1) {
			while (stk.size() && b[stk.top()][j] < b[i][j]) stk.pop();
			if (stk.size()) r[i] = stk.top();
			else r[i] = n + 1;
			stk.push(i); 
		}
		_for(i, 1, n) add(l[i] + 1, i, i, r[i] - 1, b[i][j]);
	}
	_for(i, 1, n) {
		_for(j, 1, n) {
			sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
			if (i > j) continue;
			res = max(res, sum[i][j] - a[j] + a[i]);
		}
	}
	cout << res << endl;
}

posted @ 2024-08-16 23:02 Otue 阅读(23) 评论(0) 收藏举报

刷新页面返回顶部

Otue

海到无边天作岸，山登绝顶我为峰。