重链剖分题目选讲
染色
给定一棵 \(n\) 个节点的无根树,共有 \(m\) 个操作,操作分为两种:
- 将节点 \(a\) 到节点 \(b\) 的路径上的所有点(包括 \(a\) 和 \(b\))都染成颜色 \(c\)。
- 询问节点 \(a\) 到节点 \(b\) 的路径上的颜色段数量。
颜色段的定义是极长的连续相同颜色被认为是一段。例如 112221 由三段组成:11、222、1。
这道题是树剖好题。我们来寻思如何改进树剖完成题目操作。下面是一个普通树剖,求路径和。
int query_uv(int u, int v) {
int res = 0;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
res += query(1, id[top[u]], id[u]);
u = f[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
res += query(1, id[v], id[u]);
return res;
}
我们肯定要将第 5 行线段树的 query 改成求连续段数量的函数。这个用线段树维护其实并不困难。见如下代码:
struct node {
int lc, rc, sum;
};
struct segment {
#define ls p << 1
#define rs p << 1 | 1
struct edge {
int l, r, lc, rc, sum, lazy; // lc左端点颜色,rc右端点颜色,sum颜色端数量
}tree[N * 4];
void down(int p, int x) {
tree[p].lc = tree[p].rc = tree[p].lazy = x;
tree[p].sum = 1;
}
void push_up(int p) {
tree[p].lc = tree[ls].lc;
tree[p].rc = tree[rs].rc;
tree[p].sum = tree[ls].sum + tree[rs].sum;
if (tree[ls].rc == tree[rs].lc) tree[p].sum--;
}
void push_down(int p) {
if (tree[p].lazy) {
down(ls, tree[p].lazy);
down(rs, tree[p].lazy);
tree[p].lazy = 0;
}
}
void build(int p, int l, int r) {
tree[p].l = l, tree[p].r = r;
if (l == r) return;
int mid = (l + r) >> 1;
build(ls, l, mid);
build(rs, mid + 1, r);
}
void modify(int p, int l, int r, int x) { // 区间赋值
if (l <= tree[p].l && tree[p].r <= r) {
down(p, x);
return;
}
push_down(p);
int mid = (tree[p].l + tree[p].r) >> 1;
if (l <= mid) modify(ls, l, r, x);
if (r > mid) modify(rs, l, r, x);
push_up(p);
}
node query(int p, int l, int r) { // node 返回{左端点颜色,右端点颜色,颜色端数量}这个整体信息
if (l > tree[p].r || r < tree[p].l) return {-1, 0, 0};
if (l <= tree[p].l && tree[p].r <= r) return {tree[p].lc, tree[p].rc, tree[p].sum};
push_down(p);
node x = query(ls, l, r), y = query(rs, l, r), res;
if (x.lc == -1) return y;
if (y.lc == -1) return x;
res.lc = x.lc, res.rc = y.rc;
res.sum = x.sum + y.sum - (x.rc == y.lc);
return res;
}
}tr;
考虑树剖的过程,如果这次跳的路径的底端和底端下面那个点颜色相同,则需要将颜色端数量减一。
int query_path(int u, int v) {
int res = 0, t1 = -1, t2 = -1; // 维护t1,t2,代表当前u,v下方的颜色
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v), swap(t1, t2);
node tmp = tr.query(1, id[top[u]], id[u]);
// tmp.lc是top[u]的颜色
// tmp.rc是u的颜色
res += tmp.sum;
if (t1 == tmp.rc) res--;
t1 = tmp.lc; // 更新
u = fat[top[u]];
}
if (dep[u] < dep[v]) swap(u, v), swap(t1, t2);
node tmp = tr.query(1, id[v], id[u]);
res += tmp.sum;
if (tmp.rc == t1) res--;
if (tmp.lc == t2) res--;
return res;
}
CF916E Jamie and Tree
有一棵 \(n\) 个节点的有根树,标号为 \(1\sim n\),你需要维护以下三种操作
-
1 v:给定一个点 \(v\),将整颗树的根变为 \(v\)。 -
2 u v x:给定两个点 \(u,v\) 和整数 \(x\),将 \(\operatorname{lca}(u, v)\) 为根的子树的所有点的点权都加上 \(x\)。 -
3 v:给定一个点 \(v\),你需要回答以 \(v\) 所在的子树的所有点的权值和。
这道题主要是加入了换根操作。设当前根节点为 \(root\)。
如果求 \(lca(u,v)\),你只需要知道:\(lca(u,v)\) 等于 \(lca(u,root),lca(v,root),lca(u,v)\) 当中深度最大的那个点。具体证明略。
如果是对 \(u\) 子树操作,需要分情况:
-
如果 \(u=root\),就是对整棵树进行操作。
-
如果 \(root\) 为 \(u\) 子树,见下图。
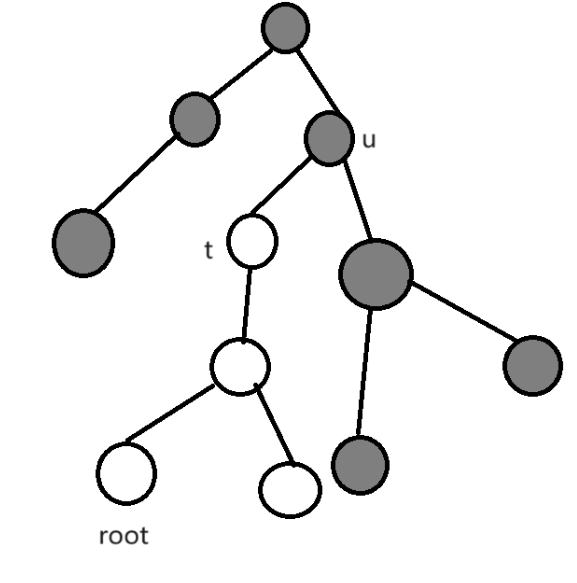
\(u\) 下方的靠近 \(root\) 的那个儿子叫做 \(t\)。可以这样操作:先把整棵树进行加,再把 t 子树减回去。灰色部分就是被操作的点。
-
如果 \(u\) 为 \(root\) 子树,则直接对 \(u\) 进行操作即可。
#include <bits/stdc++.h>
using namespace std;
#define PII pair<int, int>
#define _for(i, a, b) for (int i = (a); i <= (b); i++)
#define _pfor(i, a, b) for (int i = (a); i >= (b); i--)
#define int long long
const int N = 3e5 + 5;
int n, m, a[N], sz[N], son[N], din[N], dep[N], idx, top[N], fat[N], id[N], cc, root;
vector<int> G[N];
struct fenwick {
int c[N][2];
void add(int x, int v) {
for (int i = x; i <= N - 5; i += i & -i) {
c[i][0] += v;
c[i][1] += x * v;
}
}
void modify(int l, int r, int v) {
add(l, v);
add(r + 1 , -v);
}
int sum(int op, int x) {
int res = 0;
for (int i = x; i; i -= i & -i) res += c[i][op];
return res;
}
int query(int l, int r) {
int t1 = sum(0, l - 1) * l - sum(1, l - 1);
int t2 = sum(0, r) * (r + 1) - sum(1, r);
return t2 - t1;
}
}tr;
void dfs1(int u, int fa, int depth) {
dep[u] = depth; sz[u] = 1; fat[u] = fa; din[u] = ++cc;
for (auto v : G[u]) {
if (v == fa) continue;
dfs1(v, u, depth + 1);
sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int fa, int tt) {
top[u] = tt; id[u] = ++idx;
if (!son[u]) return;
dfs2(son[u], u, tt);
for (auto v : G[u]) {
if (v == fa || v == son[u]) continue;
dfs2(v, u, v);
}
}
int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
u = fat[top[u]];
}
if (dep[u] < dep[v]) return u;
return v;
}
int get_son(int u, int v) { // 找v的儿子在u,v路径上
while (top[u] != top[v]) {
if (fat[top[u]] == v) return top[u];
u = fat[top[u]];
}
return son[v];
}
int get_lca(int x, int y, int root) {
PII t[3];
t[0] = {dep[lca(x, y)], lca(x, y)};
t[1] = {dep[lca(x, root)], lca(x, root)};
t[2] = {dep[lca(y, root)], lca(y, root)};
sort(t, t + 3);
return t[2].second;
}
signed main() {
cin >> n >> m;
_for(i, 1, n) cin >> a[i];
_for(i, 1, n - 1) {
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(1, 0, 1);
dfs2(1, 0, 1);
_for(i, 1, n) tr.modify(din[i], din[i], a[i]);
while (m--) {
int op, u, v, x;
cin >> op >> u;
if (op == 1) root = u;
else if (op == 2) {
cin >> v >> x;
int t = get_lca(u, v, root);
if (t == root) tr.modify(1, n, x);
else if (din[root] >= din[t] && din[root] <= din[t] + sz[t] - 1) {
int tmp = get_son(root, t);
tr.modify(1, n, x);
tr.modify(din[tmp], din[tmp] + sz[tmp] - 1, -x);
}
else tr.modify(din[t], din[t] + sz[t] - 1, x);
}
else {
int res = 0;
if (u == root) res = tr.query(1, n);
else if (din[root] >= din[u] && din[root] <= din[u] + sz[u] - 1) {
int tmp = get_son(root, u);
res += tr.query(1, n);
res -= tr.query(din[tmp], din[tmp] + sz[tmp] - 1);
}
else res += tr.query(din[u], din[u] + sz[u] - 1);
cout << res << endl;
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号