单调栈与单调队列优化 dp

单调栈

将一个元素插入单调栈时，为了维护栈的单调性，需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素。

例如，栈中自顶向下的元素为 $\{0,11,45,81\}$。

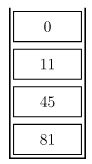
插入元素 $14$ 时为了保证单调性需要依次弹出元素 $0,11$，操作后栈变为 $\{14,45,81\}$。

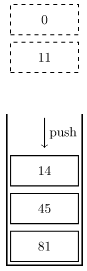
模板题：P5788 单调栈

CF547B Mike and Feet

求出所有长度为 $x(1\leq x \leq n)$ 的子序列 $a$ 中最大的子序列值。子序列值定义为这个子序列当中的最小值。

思路：
正难则反。我们枚举所有的子序列值（最小值），然后向左右两边扩展能到的最大长度区间。

举个例子，序列 1,3,2,0,5 ，如果我们当前枚举最小值 2（$3$ 号位置），那么这个区间左端点最多扩展到 $2$ 号位置，右端点最多扩展到 $3$ 号位置。区间 $[2,3]$ 就是能扩展到的最大长度区间。但是区间 $[2,4]$ 则不合法，因为此区间最小值非 $2$ 为 $0$。

一般的，若当前枚举最小值位置为 $i$，左右扩展区间为 $[l,r]$，满足 $l\leq i \leq r$，那么长度为 $1\sim r-l+1$ 的区间都能取到子序列值 $a_i$。

由于区间 $[1,r-l+1]$ 是前缀，可以不用线段树维护。这里给出两种代码。

后缀max法 $\ \ \ $ 区修点查线段树

单调队列

例题 单调队列：

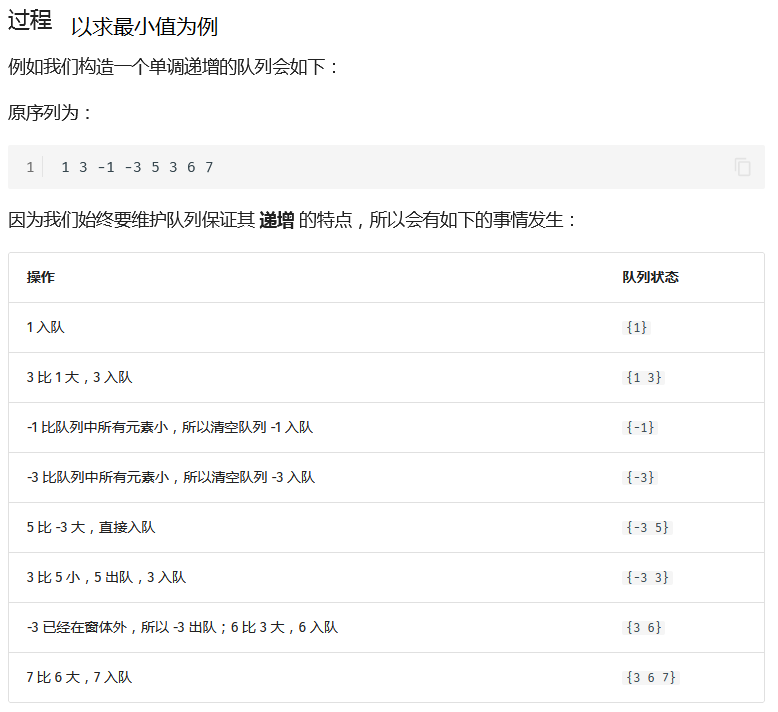
#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 5;
int n, k, a[N], q[N];

int main() {
	cin >> n >> k;
	for (int i = 1; i <= n; i++) cin >> a[i];
	int hd = 1, tl = 0;
	for (int i = 1; i <= n; i++) {
		while (hd <= tl && q[hd] <= i - k) hd++;
		while (hd <= tl && a[q[tl]] >= a[i]) tl--;
		q[++tl] = i;	
		if (i >= k) cout << a[q[hd]] <<  ' '; 
	}
	puts("");
	hd = 1, tl = 0;
	for (int i = 1; i <= n; i++) {
		while (hd <= tl && q[hd] <= i - k) hd++;
		while (hd <= tl && a[q[tl]] <= a[i]) tl--;
		q[++tl] = i;	
		if (i >= k) cout << a[q[hd]] <<  ' '; 
	}
	puts("");
}