2023.6.19 可被3整除的最大和
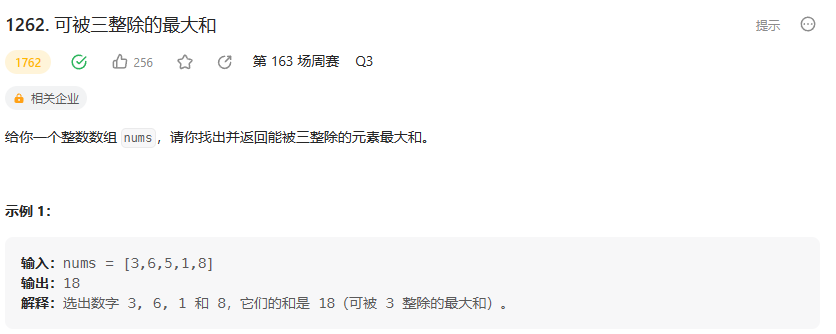
考虑动态规划,令f[i][j]表示以i开始,模3后值为j的最大和。
那么可以得到状态转移方程:
- 不取当前数,
f[i][j] = f[i + 1][j] - 取当前数,
f[i][(f[i + 1][j] + nums[i]) % 3] = f[i + 1][j] + nums[i]
目标状态:f[0][0]
impl Solution {
pub fn max_sum_div_three(nums: Vec<i32>) -> i32 {
let n = nums.len();
let mut f: Vec<Vec<i32>> = vec![vec![0; 3]; n + 1];
for i in (0..n).rev() {
// 不取这个数
for j in 0..3 {
f[i][j] = std::cmp::max(f[i][j], f[i + 1][j]);
}
// 取这个数
for j in 0..3 {
let sum = f[i + 1][j] + nums[i];
f[i][(sum % 3) as usize] = std::cmp::max(f[i][(sum % 3) as usize], sum);
}
}
f[0][0]
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号