代码随想录Day16

题目列表

• 513.找树左下角的值(LeetCode)
• 112.路径总和(LeetCode)
• 113.路径总和ii(LeetCode)
• 106.从中序与后序遍历序列构造二叉树(LeetCode)
• 105.从前序与中序遍历序列构造二叉树(LeetCode)

解题过程

513.找树左下角的值

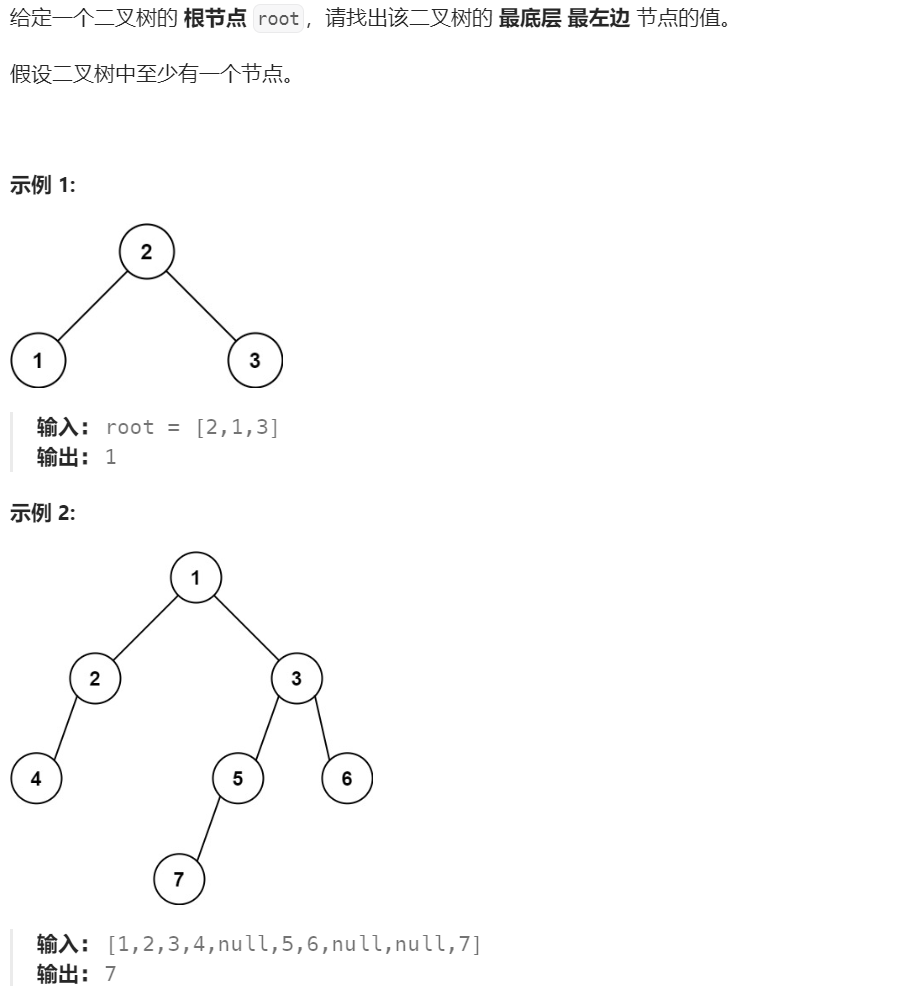
题目描述

解题思路

首先理解“最底层最左边”的意思，也就是深度最深的一层的第一个叶子，可能是左叶子，也可能是右叶子。
所以要保证在遍历这棵树的时候始终是左边优先。
方法1：使用递归与回溯
递归函数参数：根节点，每一个节点的深度
终止条件：遍历到了叶子节点
递归逻辑：先遍历左孩子，再遍历右孩子，注意每遍历完一个叶子节点后要回溯。

注意事项

1.递归终止条件中 depth > maxDepth

必须是大于，如果等于，就有可能返回最深的一层最右边的节点的值（如果最深的一层不止一个节点的话）。

代码展示

class Solution {
    int maxDepth = -1;
    int value = 0;
    public int findBottomLeftValue(TreeNode root) {

        find(root,0);
        return value;

    }
    public void find(TreeNode node, int depth){
        if(node.left == null && node.right == null){
            if(depth > maxDepth){
                maxDepth = depth;
                value = node.val;
            }
            return;
        }
        if(node.left != null) {
            depth++;
            find(node.left,depth);
            depth--;
        }
        if(node.right != null) {
            depth++;
            find(node.right,depth);
            depth--;
        }
    }
}

112.路径总和

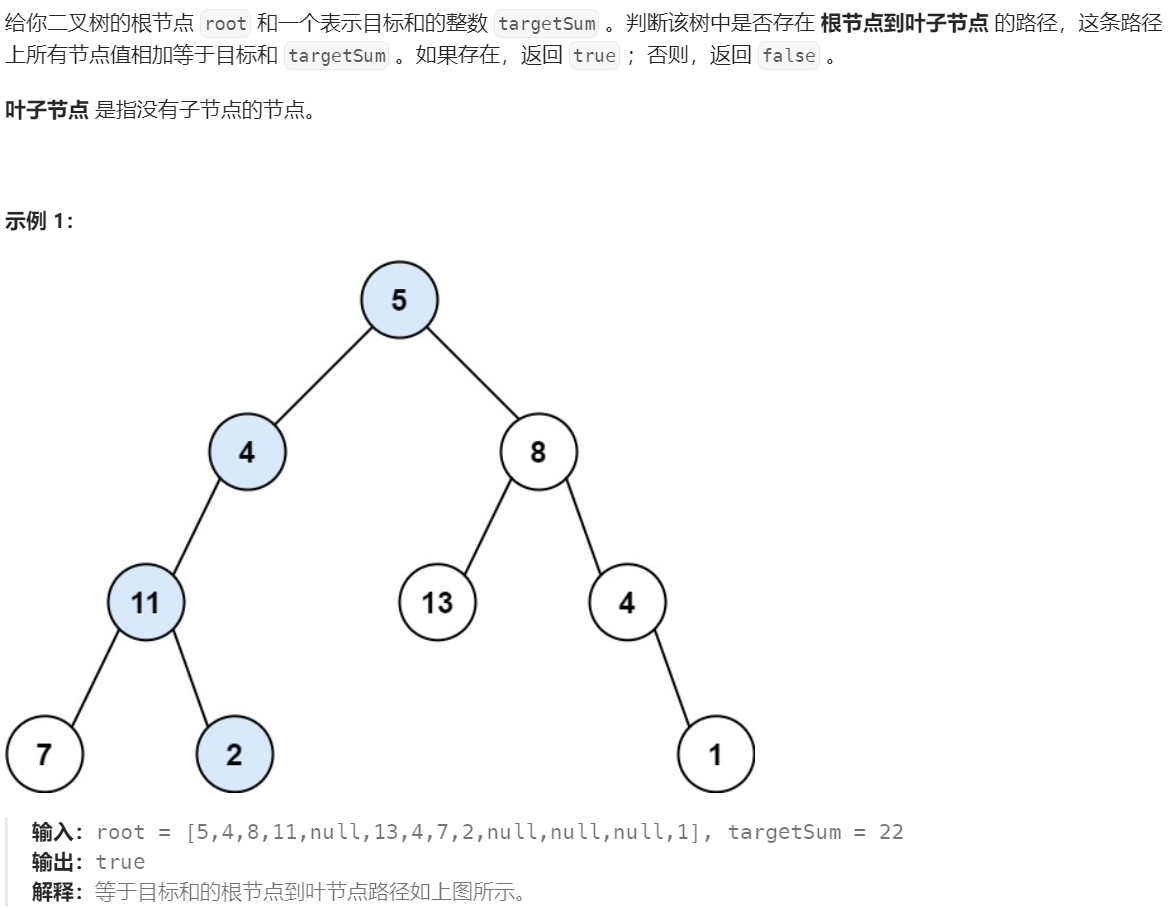
题目描述

解题思路

依旧是要去遍历这棵树从根节点到叶节点的路径，不过要在这个过程中返回是否有一条路径节点值之和等于目标值的情况。
采用递归：

• 递归函数参数与返回值：返回值是 true 或 false ,代表找到或未找到；参数应该是树的节点，以及一个计数器，可以让这个计数器在一开始等于目标值，每遍历一个节点就减去这个节点的值。
• 终止条件：当前节点是叶子节点，而且减去它的值之后计数器为0。
• 递归逻辑：当前节点左孩子不为空就让左孩子进入递归，在这里可以直接判断一下，如果是 true 就表示左孩子已经是叶子节点而且找到了这条路径，就可以提前返回 true 了。如果是 false，就证明这条路径不是，count 加上这个节点的值（回溯）。右孩子逻辑也是这样。

代码展示

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root == null) return false;
        return has(root,targetSum - root.val);
    }
    public boolean has(TreeNode node,int count){
        if(node.left == null && node.right == null && count == 0) return true;
        if(node.left == null && node.right == null) return false;

        if(node.left != null){
            count -= node.left.val;
            if(has(node.left, count)) return true;
            count += node.left.val;
        }
        if(node.right != null){
            count -= node.right.val;
            if(has(node.right, count)) return true;
            count += node.right.val;
        }
        return false;
    }
}

113.路径总和ii

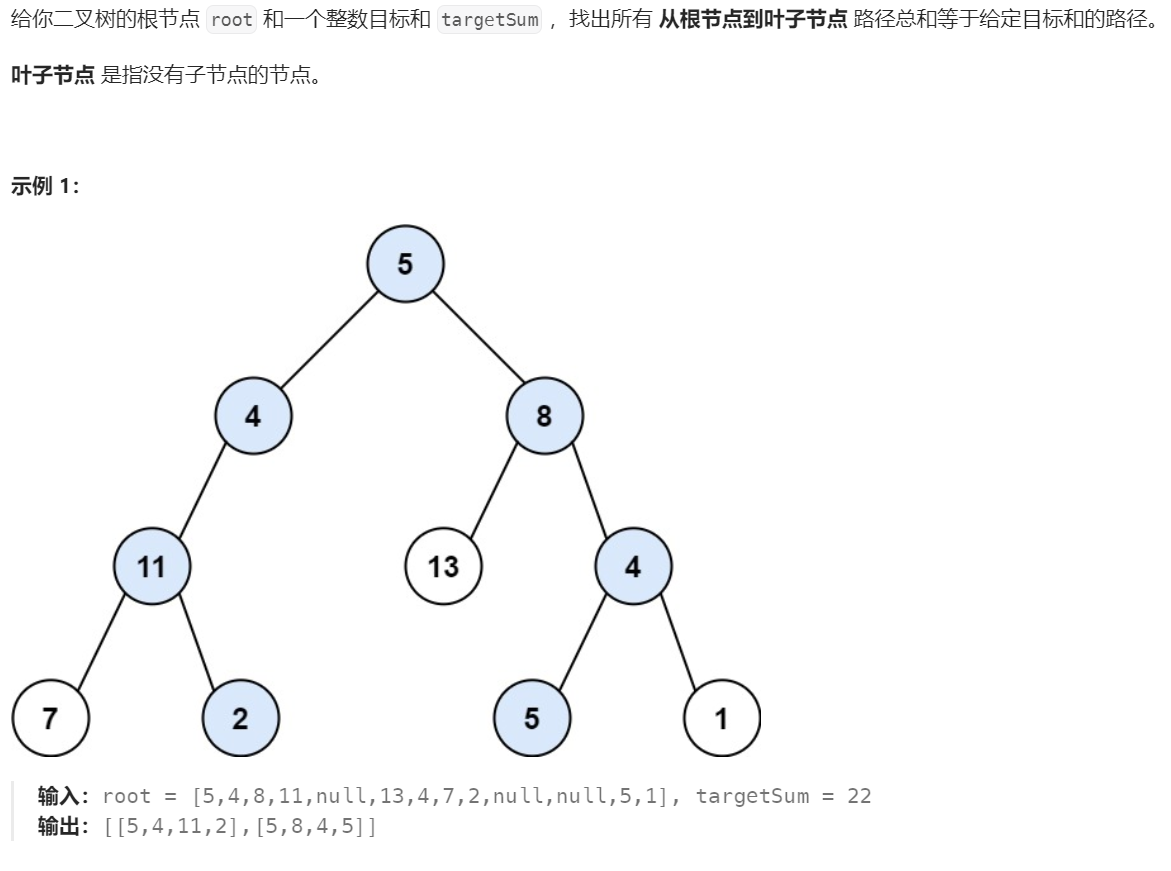
题目描述

解题思路

这个题目和上一个差不多思路，但是要记录符合要求的路径，所以递归函数就不用返回值了，回溯的时候除了考虑count还要考虑路径列表path.
考虑到在root不为null的情况下，任何一条路径都会包含root.val，所以可以在递归之前直接path.add(root.val).
要及时存储path的快照。

代码展示

class Solution {
    List<List<Integer>> res;
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        res = new ArrayList<>();
        if(root == null) return res;
        path.add(root.val);
        found(root,targetSum - root.val);
        return res;
    }
    public void found(TreeNode node, int count ) {
        
        if(node.left == null && node.right == null && count == 0){
            res.add(new ArrayList<>(path));
            return;
        }
        if(node.left != null){
            count -= node.left.val;
            path.add(node.left.val);
            found(node.left, count);
            count += node.left.val;
            path.remove(path.size() - 1);
        }
        if(node.right != null){
            count -= node.right.val;
            path.add(node.right.val);
            found(node.right, count);
            count += node.right.val;
            path.remove(path.size() - 1);
        }
    }

}

106.从中序与后序遍历序列构造二叉树

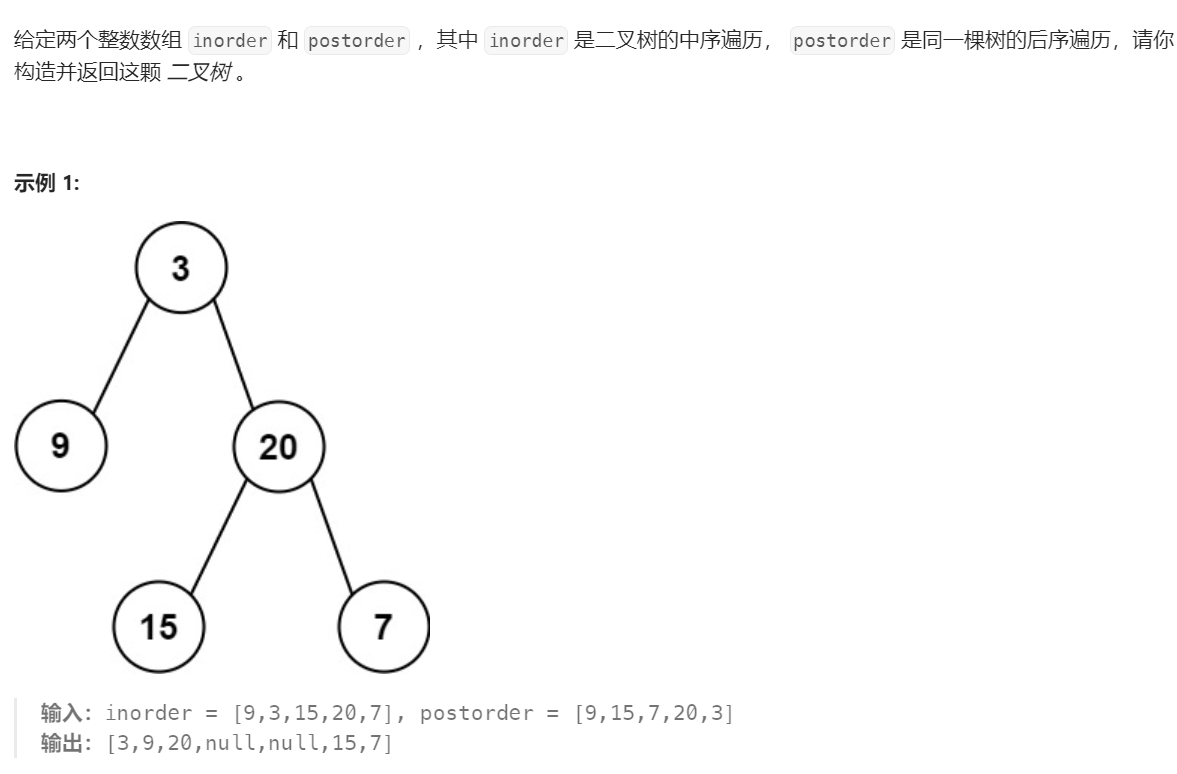
题目描述

解题思路

第一步：如果数组大小为零的话，说明是空节点了
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

代码展示

/**
    第一步：如果数组大小为零的话，说明是空节点了。
    第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
    第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
    第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
    第五步：切割后序数组，切成后序左数组和后序右数组
    第六步：递归处理左区间和右区间 */
class Solution {
    Map<Integer, Integer> map = new HashMap<>();
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if( postorder.length == 0) return null;
        for(int i = 0; i < inorder.length; i++){
            map.put(inorder[i], i);
        }
        
        return find(inorder,0,inorder.length,postorder,0,postorder.length);
    }
    public TreeNode find(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd){
        if(inBegin >= inEnd || postBegin >= postEnd) return null;
        int rootValue = postorder[postEnd - 1];
        TreeNode root = new TreeNode(rootValue);
      
        int middleIndex = map.get(rootValue);
        
        root.left = find(inorder, inBegin, inBegin + middleIndex, postorder, postBegin, postBegin + (middleIndex - inBegin));

        root.right = find(inorder, middleIndex + 1, inEnd, postorder, postBegin + (middleIndex - inBegin), postEnd - 1);
        return root;
    }
}

105.从前序与中序遍历序列构造二叉树

题目描述

解题思路

第一步：如果数组大小为零的话，说明是空节点了
第二步：如果不为空，那么取前序数组第一个元素作为节点元素
第三步：找到前序数组第一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组
第五步：切割前序数组，切成前序左数组和前序右数组
第六步：递归处理左区间和右区间
前序和上一题后序起相似的作用，但中序永远是铁打的中序。

代码展示

class Solution {
    Map<Integer, Integer> map = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder.length == 0) return null;
        for(int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }

        return find(inorder, 0, inorder.length, preorder, 0, preorder.length);
    }
    public TreeNode find(int[] inorder, int inBegin, int inEnd, int[] preorder, int preBegin, int preEnd){
        if(inBegin >= inEnd || preBegin >= preEnd) return null;

        int rootValue = preorder[preBegin];
        TreeNode root = new TreeNode(rootValue);

        int middleIndex = map.get(rootValue);
        int leftLength = middleIndex - inBegin;
        root.left = find(inorder, inBegin, middleIndex, preorder, preBegin + 1, preBegin + 1 + leftLength);
        root.right = find(inorder, middleIndex + 1, inEnd, preorder, preBegin + 1 + leftLength, preEnd);
        return root;
    }
}

参考资料

代码随想录