代码随想录Day14

题目列表

• 226.翻转二叉树(LeetCode)
• 101.对称二叉树 (LeetCode)
• 104.二叉树的最大深度(LeetCode)
• 111.二叉树的最小深度 (LeetCode)

解题过程

226.翻转二叉树

题目描述

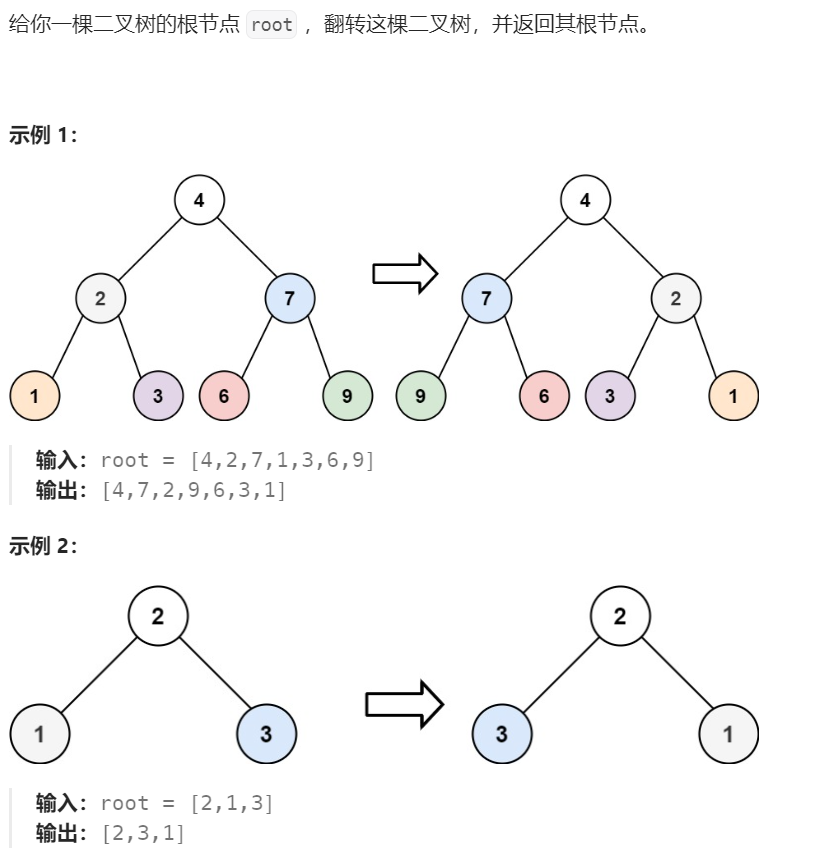
解题思路

反转二叉树，也就是反转每一个节点的左右孩子，递归实现，使用前序或后序遍历。

注意事项

使用中序遍历需要额外的逻辑，因为有的节点左右孩子会被反转两次。

代码展示

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) return null;

        swap(root);
        invertTree(root.left);
        invertTree(root.right);

        return root;
    }

    public void swap(TreeNode cur){
        TreeNode temp = cur.left;
        cur.left = cur.right;
        cur.right = temp;
    }
}

101.对称二叉树

题目描述

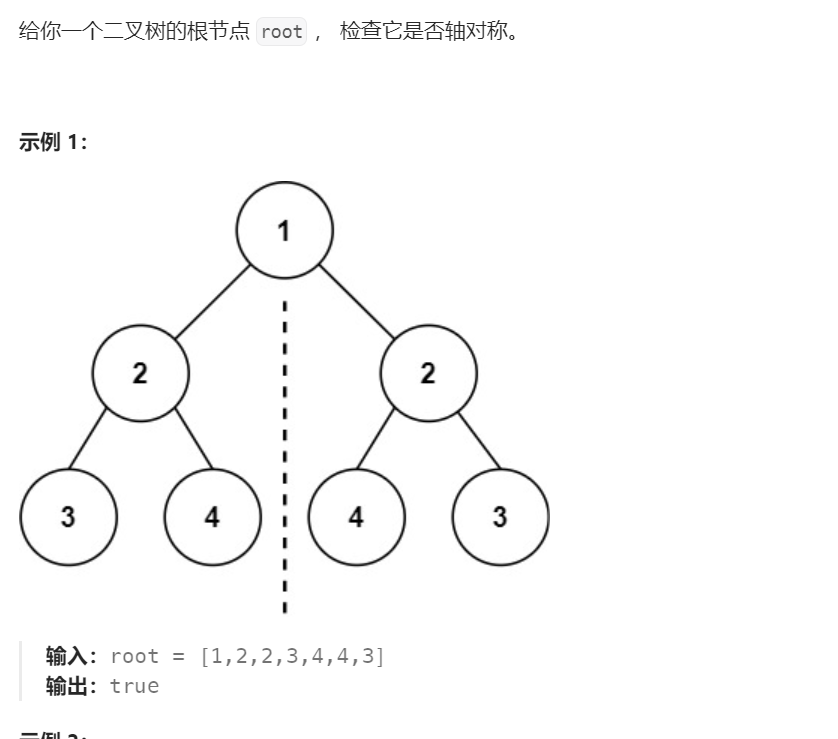
解题思路

从示例可以看出，二叉树对称也意味着根节点的左右子树可以相互翻转，也可以理解为左右两个子树的最外侧一致，最内侧也一致。可以使用递归来判断：
递归函数的参数：相互对应的左右子树的孩子（左树的左孩子对应右数的右孩子，左树的右孩子对应右数的左孩子），调用时传入根节点的左右孩子。
递归终止条件：这两个孩子不对称，或者两个孩子都是null(对称，但不用再递归了)。
递归逻辑：不断比较左树的左孩子与右数的右孩子是否一致，左树的右孩子与右树的左孩子是否一致。返回比较结果的逻辑与的结果。

注意事项

后序遍历

因为一个树对称的条件是它的左右子树可以翻转，也就意味着在没有比较完左右子树的情况下是无法确定这个节点的状态的。
所以对于中间节点的处理必须放在最后。

代码展示

class Solution {
    public boolean isSymmetric(TreeNode root) {

        return compare(root.left,root.right);
    }
    public boolean compare(TreeNode left, TreeNode right){
        if(left == null && right != null){
            return false;
        }
        else if(left != null && right == null){
            return false;
        }
        else if(left == null && right == null){
            return true;
        }
        else if(left.val != right.val){
            return false;
        }

        boolean outside = compare(left.left, right.right);
        boolean inside = compare(left.right,right.left);
        return outside && inside;
    }
}

104.二叉树的最大深度

题目描述

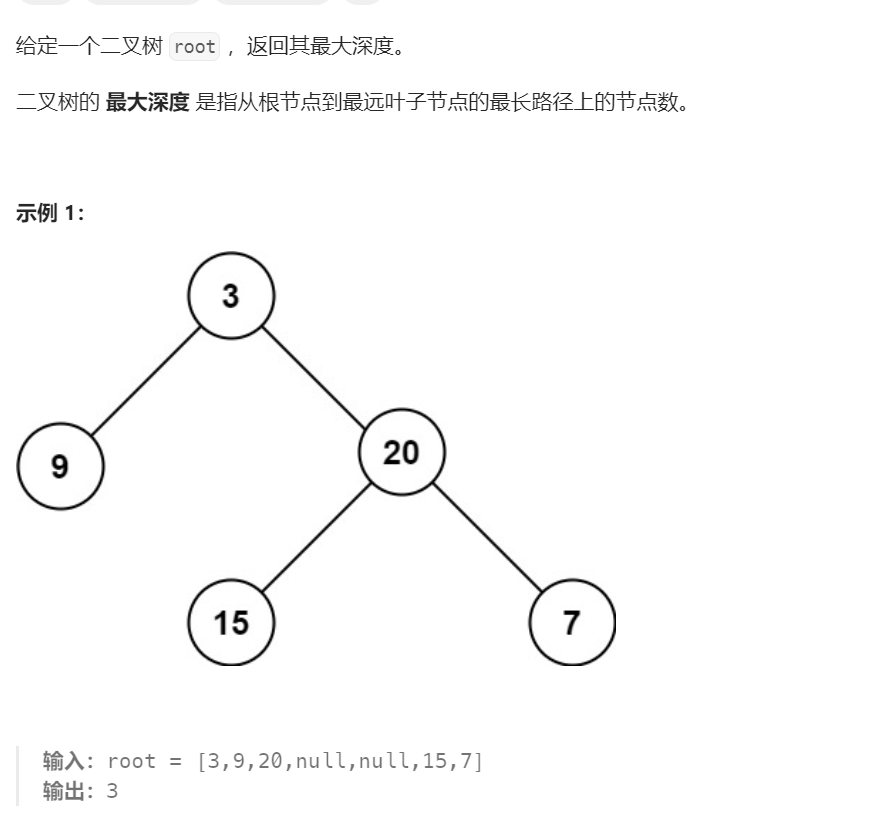
解题思路

深度：该节点到根节点的最长简单路径边的节点数
高度：该节点到叶子节点的最长简单路径边的节点数
可以看出，一棵树的最大深度是也就是根节点的高度。
求一个节点的高度，要使用后序遍历，不断给parent节点返回子树的高度，一直到根节点。

代码展示

class Solution {
    public int maxDepth(TreeNode root) {
        return rootHeight(root);
    }
    public int rootHeight(TreeNode node){
        if(node == null) return 0;

        int leftHeight = rootHeight(node.left);
        int rightHeight= rootHeight(node.right);
        return 1 + Math.max(leftHeight,rightHeight);
    }
}

111.二叉树的最小深度

题目描述

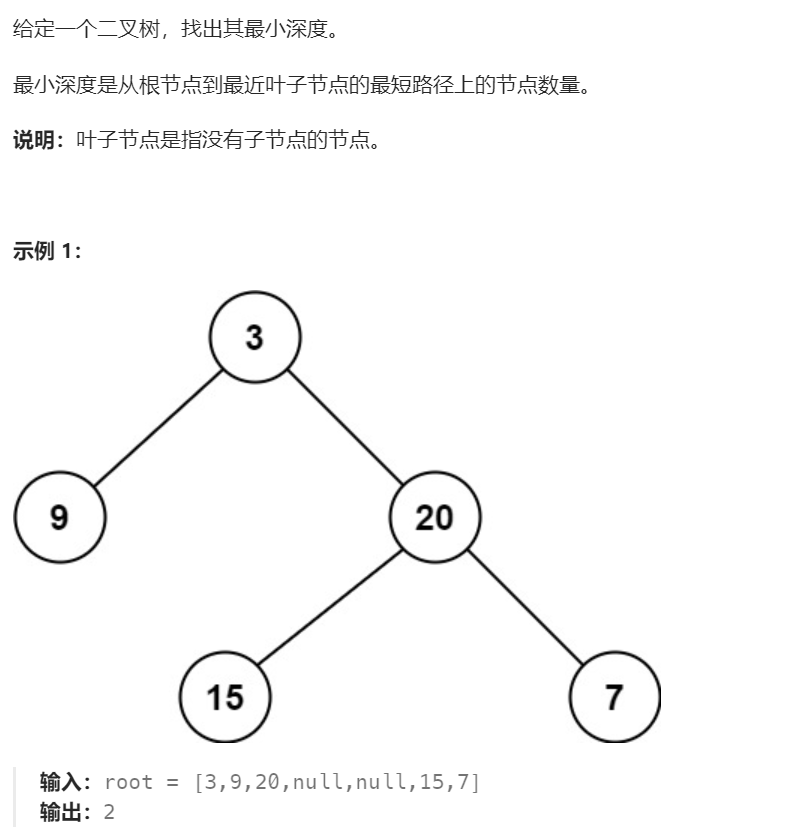
解题思路

最小深度，也就是根节点到最近的叶子节点的最短路径边的节点数。

注意事项

叶子节点

没有左右孩子的节点才算是叶子节点，所以在递归逻辑中，要判断当前节点是不是叶子节点。

代码展示

class Solution {
    public int minDepth(TreeNode root) {
        return minHeightForRoot(root);
    }
    public int minHeightForRoot(TreeNode node){
        if(node == null) return 0;

        int leftHeight = minHeightForRoot(node.left);
        int rightHeight = minHeightForRoot(node.right);

        if(node.left == null && node.right != null){
            return 1 + rightHeight;
        }
        if(node.left != null && node.right == null){
            return 1 + leftHeight;
        }
        int result = 1 + Math.min(leftHeight,rightHeight);
        return result;
    }
}

参考资料

代码随想录