动态规划---求解具体方案

一：求解具体方案

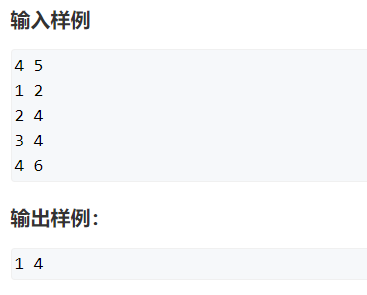
（一）题目详解

（二）解题思路

首先我们要确定如何输出其最优解的具体方案：

可以这样判断，如果f[i][j]等于f[i-1][j] 则说明不选第i个物品，如果f[i][j]等于f[i-1][j-v[i]]+w[i] 则说明选第i个物品，通过这样的判断来得出完整的路径。

由于题目要求输出字典序最小的方案，所以我们应该以物体编号从小到大的顺序输出结果。（原本的是优先求字典序最大）

（三）算法实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int f[N][N],v[N], w[N];    //因为我们后面是后向前处理物品，所以我们需要提前保存物品信息，使用v,w数组
int n, m;

int main()
{
    cin >> n >> m;    //输入物品组数、背包最大容量

    for (int i = 1; i <= n; i++)    //提前保存物品信息
        cin >> v[i] >> w[i];

    for (int i = n; i >= 1; i--)    //循环物品组数
        for (int j = 0; j <= m; j++)
        {
            f[i][j] = f[i + 1][j];
            if (j>=v[i])
                f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }

    //求解路径
    int vol = m;    //容量
    for (int i = 1; i <= n;i++)　　//因为我们上面是从n->1,所以我们的最终结果保存在1物品中，我们使用f[1][m]获取最大价值，之后向后回溯即可
        if (f[i][vol]==f[i+1][vol-v[i]]+w[i])
        {
            cout << i << " ";
            vol -= v[i];
        }
    system("pause");
    return 0;
}