动态规划---多重背包
现在完全背包、多重背包都是和01背包进行对比
一:多重背包(1)
(一)题目要求


(二)多重背包算法实现(由于数据不大,所以我们可以使用3层循环进行处理)
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m; int f[N]; //全局变量,被初始化0 int main() { cin >> n >> m; //初始化物品数量和背包容积 for (int i = 1; i <= n; i++) { int w, v, s; //物品体积、价值、数量 cin >> w >> v >> s; for (int j = m; j >= w; j--) //注意:需要添加我们将判断条件提到这一步当中,保证剩余容量大于当前物品的体积 for (int k = 0; k <= s&&k*w <= j;k++) f[j] = max(f[j], f[j - k*w] + k*v); //对应不选和选 } cout << f[m]<<endl; system("pause"); return 0; }
和我们前面完全背包问题中的朴素算法类似。
二:多重背包二进制拆分方法
(一)题目要求


简单分析,如果使用方法一,则需要1000×2000×2000=10^9会超时处理。
(二)二进制拆分方法
1到n以内的数字,能够通过 n 内的进制数组合得到,比如 9以内的二进制数有 1 2 4 8,可以自己在草稿纸上试一下, 3能通过 1 + 2 得到,5能通过1 + 4 得到,6能通过 2 + 4得到。
把Ci个物品分解成p+2个,即若干个2的幂次方为系数的体积(对下面的这些体积进行0/1背包):
20*Vi+...+2p*Vi+Ri*Vi
所以,我们可以利用二进制数的拆分求出所有 n 以内的数;下面是拆分的过程:
9 - 1 = 8; 8 - 2 = 6; 6 - 4 = 2 ; 2 - 8 < 0; 那么要求的 9 以内的二进制数就是 1,2, 4,2,这几个二进制是能够组成 9以内包括 9 的所有整数,然后通过 w[ i ] 乘以这些二进制数,把他们当作一件物品来做01背包的处理。
总之:我们通过上面的二进制拆分方法,我们可以使用log(n)个数表示全部的取值个数范围,虽然我们增加了物品个数<比如第i个物品有9个,转换为1、2、4、2为4个物品,每个物品的体积、价值需要相乘拆分后的个数,这样我们在后面01选取的时候可以选取所有的物品i的所有个数情况>,但是我们将多重背包问题转换为了01背包问题,在后面算法中,我们不需要三层循环处理。复杂度变为:n∗m∗log(num),而不是原来的n*m*num
(三)多重背包问题之二进制拆分算法实现
#include <iostream> #include <algorithm> #include <vector> using namespace std; const int N = 2020; int n, m; int f[N]; //全局变量,被初始化0 struct Good{ int w, v; }; int main() { vector<Good> goods; cin >> n >> m; //初始化物品数量和背包容积 for (int i = 1; i <= n; i++) //初始化二进制拆分后的数量和价值 { int w, v, s; cin >> w >> v >> s; for (int k = 1; k <= s; k *= 2){ //注意:k从1开始,01背包会进行选或者不选,当所有拆分都不选择,那么就是没有选择这个物品 s -= k; goods.push_back({ w*k, v*k }); //插入当前二进制拆分物品 } if (s > 0) goods.push_back({ s*w, s*v }); //插入最后剩余的个数 } //开始进行01背包求解问题 for (auto g:goods) for (int j = m; j >= g.w; j--) //注意:需要添加我们将判断条件提到这一步当中,保证剩余容量大于当前物品的体积 f[j] = max(f[j], f[j - g.w] + g.v); //对应不选和选 cout << f[m]<<endl; system("pause"); return 0; }
三:多重背包之单调队列优化问题
(一)题目分析

简单分析,如果使用二进制拆分方法,则需要1000×20000×log(20000)=3×10^8,会出现超时现象
(二)单调队列优化讲解
https://leetcode-cn.com/circle/article/V5qkAa/(不错哦)
https://www.bilibili.com/video/BV1fK4y1b7Xt?from=search&seid=2882629087440342681(也可以)
相比较完全背包问题的状态转移方程:

完全背包,也可以写成下面多重背包的形式,但是最后结束的项表示的是在剩余空间下可选的当前物品数为k,还是有所区别的f(i-1,j-kv)+kw
这个判断条件是因为完全背包没有对物品进行限制。
多重背包状态转移方程:
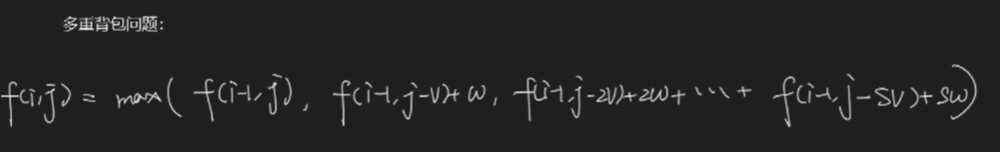
都是相对于第i-1层进行的,第一项f(i-1,j)表示没有选择,第二项中f(i-1,j-v)+w表示选择了一个第i种的物品,第三项f(i-1,j-2v)+2w表示选择了两个当前层的物品,.....,最后一项表示了我们最大可以选择的当前层物品数是s个
而s的取值,来自于我们在单调队列中滑动窗口大小的设置。
我们可以发现,求解f(i,j)过程中,max中各项的j,j-v,j-2v,....如果关于对v求余的话,都可以归为j这一组
多重背包状态转移方程变形:
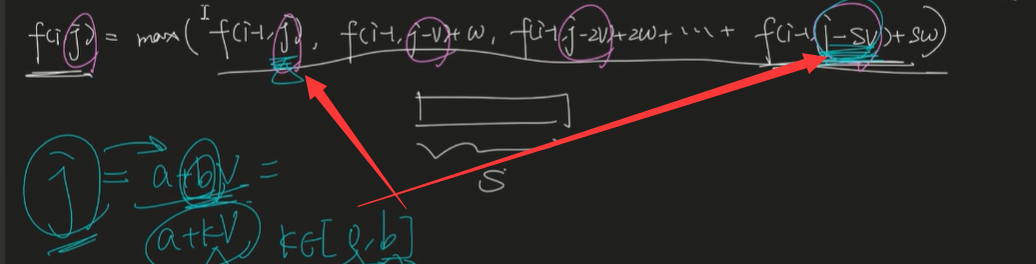
我们后面的循环都是针对这个k进行的。而最终形式如下:

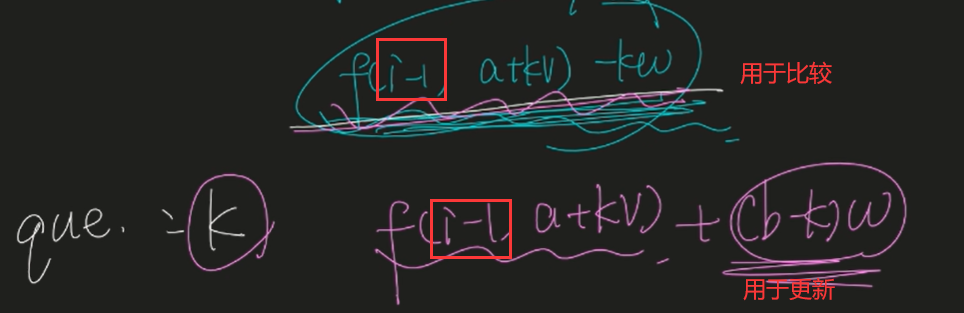
通项如下:由于b在内层循环中为常量,所以我们可以忽略。因此比较最大值时使用第3项即可,更新第i层f值时还是需要使用第一项

单调队列:存放的是k值。注意:我们都是使用i-1层的数据进行更新当前i层的数据
(三)算法实现
#include <iostream> #include <algorithm> #include <vector> using namespace std; const int N = 2020; int n, m; int f[N],g[N]; //全局变量,被初始化0 int que[N]; //单调队列 int main() { cin >> n >> m; //初始化物品数量和背包容积 for (int i = 1; i <= n; i++) //初始化二进制拆分后的数量和价值 { int v, w, s; cin >> v >> w >> s; memcpy(g, f, sizeof f); //备份i-1层的数据信息 for (int r = 0; r < v;r++) //循环前面余数部分 { int head = 0, tail = -1; //设置队列首尾指针 //开始循环第i-1层同余数r的所有数据,得到第i层信息 for (int k = 0; r+k*v <= m ;k++) //r+k*v<m表示没有超过背包容量 { //开始实现单调队列,先了解单调队列 if (head <= tail && k - que[head] > s) //如果滑动窗口已满,则出队队首元素---后面判断没有懂???? head++; while (head <= tail && g[r + k*v] - k*w > g[que[tail] * v + r] - que[tail] * w) //比较大小,当前元素大于队尾,则队尾出队 tail--; //开始入队 que[++tail] = k; //单调队列实现完成 f[r + k*v] = g[r + que[head] * v] + (k - que[head])*w; //更新元素,这里k就是图中b,为v的倍数值 } } } cout << f[m] << endl; system("pause"); return 0; }
???
/* 由于同余的数组元素数量可能超过同一物品的使用次数s。 k - que[head] > s 实际为 ((r + k * v) - (r + que[head] * v)) / v > s ,((r + k * v)当前遍历到的数组元素下标,(r + que[head] * v))当前遍历到下标之前的最大数组元素的下标。 */


 浙公网安备 33010602011771号
浙公网安备 33010602011771号